三角函数及解三角形核心考点测试卷A 参考答案

一、选择题

1.B 2.B 3.C 4.B 5.B 6.C

7.B 8.A 9.D 10.D 11.D 12.B

二、填空题

13.

三、解答题

17.解法一：(1)由m⊥n得2 cosαsinα=0，sinα=2 cosα，代入cos2α+sin2α=1，得5 cos2α=1，且

解法二：(1)由

18.(1)因为A，B，C为三角形的内角，所以A+B+C=π。

又因为0＜C＜π，所以

19.以O为原点，以为x轴正方向，建立如图1所示的平面直角坐标系。

(1)设D(t，0)(0≤t≤

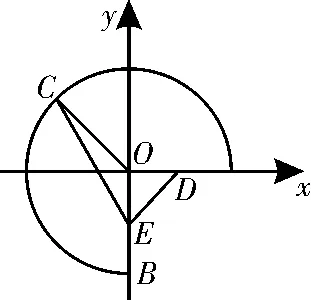
图1

20.(1)由已知条件知，当取得最大值1，从而有，即8ω=12k+4，k∈Z。

又由题意可得该函数的最小正周期T满足：且，于是有，满足0＜12k+4≤6的正整数k的值为0，于是

21.(1)因为，所以，即，又所以

由余弦定理得a2=b2+c2-2b c·，所以，故

22.由和差公式可知