基于范希尔几何理论的中学数学教学研究

陈玉莲 令狐泓 严艳华

[摘  要] 范希尔几何理论是重要的数学学习理論，对培养学生几何直观有着重要的教学意义. 深入研究分析其理论内涵和五个教学阶段，并以“正弦定理”为例设计教学，基于案例提出三点教学思考：一是厘清范希尔的五个教学阶段，二是有效结合信息技术，三是以学生为主，旨在更好地指导教学.

[关键词] 范希尔几何理论;教学设计;正弦定理

[?]问题提出

《义务教育数学课程标准（2011年版）》不仅将几何直观作为课标十个核心关键概念之一，而且把“图形与几何”划分到四大课程内容当中[1]，其充分体现了几何图形学习的重要性. 2018年，教育部颁布了《普通高中数学课程标准（2017年版）》，将直观想象作为六大核心素养之一[2]. 可见，加强学生几何直观素养培养的重要性不言而喻.几何内容作为数学学习的重要内容之一，无论是在实际教学内容，还是在高考的考查中，都占据着相当大的比重. 然而，从目前教学现状来看，绝大多数学生的几何水平并不理想，这不仅暴露了学生直观想象能力的缺乏，而且阻碍了学生逻辑推理能力的发展. 针对学生的几何学习困境，积极探索解决方法，以发展学生几何推理能力，刻不容缓.范希尔几何理论自提出以来，一直是几何教与学的关注点，是数学教育界研究的热点话题. 因此，基于范希尔几何理论框架，对“正弦定理”教学进行分析和设计，以期为几何教学提供参考.

[?]范希尔几何理论

范希尔几何理论主要包含两个内容：一是几何思维的五个水平，既可用来判断学生几何思维现状，也可指导教学活动设计;二是与五个水平对应的五个教学阶段，这就为几何教学搭建了一种模式和框架[3]. 研究基于五个教学阶段，完成几何教学设计，以起到提升学生几何直观能力的作用. 五个教学阶段分别如下：

阶段1：学前咨询. 对于学习对象，教师与学生双向了解，教师帮助学生如何认知指导语，并阐述和厘清要学习的课堂内容，为熟悉相应知识做铺垫.

阶段2：引导定向. 教师合理设计教学活动细节和顺序，明确学生的学习方向，让学生认识到整个活动过程的结构特征.

阶段3：阐明. 经历了前面的探究活动过程，教师给予启发诱导，学生增长学习经验，并明确词汇的含义和意义，能够充分表达个人对该结构的意见，逐步形成学习的关联体系.

阶段4：自由定向. 面对相对复杂的作业习题能够用不同的方法完成任务，在积极探索解决方案和方法中，收获活动经验.

阶段5：整合. 学生回顾自己解决问题的过程，形成一定的思想和方法，并将相关对象和内容进行内化处理，从而进入一个全新的思维领域，得到成长.

[?]正弦定理的教学设计

阶段1：学前咨询.

设计1：设置情境，激发兴趣.

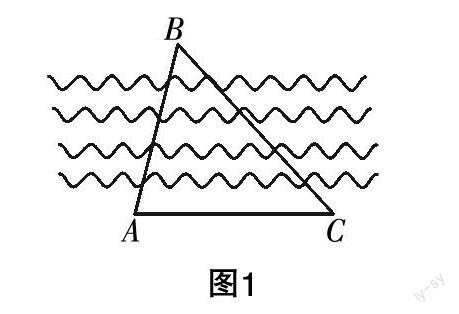
如图1所示，设A，B两点在河的两岸，在A的河岸同一侧取一点C，已知AC=450 m，如何测出A，B两地的距离？

学生：测出角A和角C.

教师：假如现在测出∠A=75°，∠C=45°，怎么求解A，B两地的距离呢？

学生：利用初中相似三角形知识，画出三角形A′B′C′，其中A′C′=4.5 cm，∠A′=75°，∠C′=45°，通过测量，可以得出A′B′=3.67 cm，再利用相似三角形性质可得AB=367 m.

教师：做得不错. 通过初中相似三角形知识，能够帮助我们解决该问题.我们初中也学过直角三角形相关知识，能否利用直角三角形知识求解呢？

学生：过A作AD⊥BC于D.此时，将△ABC分成两个三角形，接着能够利用直角三角形相关知识解决此类问题（过程略）.

教师：很棒！上述方法都是基于初中知识而来的，那么这类问题还可以用什么方法来解决呢？（设置悬念）

设计2：回顾初中“边与角”关系.

教师：对于一个三角形，我们如何判断哪个是最小角、哪个是最大角？哪个是最短边、哪个是最长边？能否总结其中蕴含的规律？

学生：可以利用“大边对大角，小边对小角”来判断.

教师：大边、大角，小边、小角！这仅仅是直观的定性描述，到底如何准确量化边和角的关系呢？对此，这节课我们不得不重新研究三角形.

设计意图：一方面，通过情境导入，利用实际生活问题，复习初中所学相关内容，起到“温故知新”的作用，同时培养学生解决实际问题的能力.另一方面，利用问题引出正弦定理，让学生对本节课的学习内容产生兴趣.

阶段2：引导定向.

设计3：直角三角形中“边与角”的关系.

教师：在RT△ABC中，已知∠A所对的边为a，∠B所对的边为b，∠C所对的边为c. 我们学过正弦、余弦、正切，今天我们从正弦出发，在图2中，我们能发现∠A，∠B，∠C，a，b，c之间有何数量关系吗？

学生：可以得到sinA=和sinB=，即==c.

教师：根据式子形式，能够发现什么问题？c与sinC和上式能否建立等式关系？

学生：等式左右两边具有一定的对称关系.由上式可知==，而sinC=sin90°=1，因此==.

教师：非常棒！

教师：通过上述分析，我们发现三角形中居然蕴含着这种边角关系.既然我们已经找出了这个正弦定理，那么这节课就上到这里了，下课！

学生：（学生感到困惑——为何早早下课，并发现了问题）不对！我们仅仅针对直角三角形发现了该关系式.

教师：其他三角形是否具备这样的关系式？

此时学生处于疑惑当中，教师利用几何画板，通过拖动A点，改变三角形形状，使边与角不断变化，如图3所示. 学生通过观察，能够发现各边与其对角的正弦值之比是相等的，即说明上式在直角三角形、锐角三角形、钝角三角形中都成立.

设计意图：通过引导使学生猜想得出等式==，以直角三角形为研究对象，实现特例分析，經历数学抽象的过程. 同时，通过几何画板动态演示，让抽象的内容可视化，学生由此发现规律，降低学生对抽象问题的理解难度.

阶段3：阐明.

设计4：探究锐角三角形、钝角三角形.

通过设计3的内容展现，学生能够得出==对所有三角形都是成立的，但为了加深学生的认知，让学生认识到数学的严谨性，接下来，基于锐角三角形和钝角三角形对上述式子进行论证.

教师：前面我们是通过直角三角形得到的==，那么在锐角三角形中怎么去证明它是成立的呢？

学生：继续利用直角三角形！

教师：具体怎么做？

学生：通过图4所示，我们发现sinC=，sinB=，即AD=bsinC=csinB，即=.

教师：那么怎么找？

学生：同样地，如图5所示，过点B作BE⊥AC于E，能够得到sinC=，sinA=，BE=asinC=csinA，即=，因此==.

教师：非常好. 接下来，大家试着在钝角三角形中进行证明.

学生：如图6所示. 延长CB，过A点作AD⊥CD，垂足为D，可得AD=bsinC=csin∠ABD=csin（180°-∠ABC）=csin∠ABC，即=. 同理可得=. 故==.

即可得出正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即==.

设计意图：通过对锐角三角形和钝角三角形中正弦定理的证明，体现了数学的严谨性.在证明过程中，教师适当启发诱导，让学生经历正弦定理的证明过程，养成独立思考的习惯，培养学生分析和解决问题的能力.

阶段4：自由定向.

设计5：正弦定理的应用探索.

问题1：解三角形.一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素.已知三角形的几个元素，求其他元素的过程叫做解三角形.

题1：在△ABC中，角A，B，C的对边分别是a，b，c，若A∶B∶C=1∶2∶3，则a∶b∶c等于（  ）

A. 1∶2∶3 B. 2∶3∶4

C. 3∶4∶5D. 1∶∶2

题2：在△ABC中，A=60°，a=，b=，则B等于（  ）

A. 45°或135°B. 60°

C. 45° D. 135°

题3：在△ABC中，b=1，c=，C=，则a=________.

问题2：正弦定理的使用条件.

教师：通过上面的例题，发现正弦定理能够帮助我们解决哪种类型的三角形问题？

学生：已知三角形任意两角及一边，可解出其余边和角.

教师：还有吗？

学生：已知三角形任意两边和其中一边的对角，可解出其余边和角.

教师：回答得很好. 通过习题训练，大家都明确了正弦定理的相关应用.那么已知两边和夹角，怎么解三角形？

（学生陷入沉思）

教师：这个问题现在我们还无法解决，需要下节课学习余弦定理后来解决该问题.

设计意图：问题1的提出，学生能够在实际解题中体验正弦定理的应用，并巩固所学知识. 问题2基于问题1的习题训练，让学生通过学习活动，提出并归纳正弦定理的使用条件. 同时，设置悬念问题，为下节课学习做好铺垫，激发学生对下节课学习的兴趣.

阶段5：整合.

设计6：以问答形式总结反思.

通过问答形式让学生归纳和总结本节课的内容，回顾正弦定理的证明过程.总结其中涉及的知识点、思想和方法，并强调正弦定理的使用条件.

提出课后思考问题：（1）还有没有其他方法可以证明正弦定理？（2）已知两边和夹角，怎么解三角形？

设计意图：通过学生自己归纳和总结，以巩固和复习这节课内容，收获思想和方法，并提升学生学习的积极性.利用课后思考问题，增强学生课后探索求知的兴趣.

[?]教学反思

基于范希尔几何理论设计正弦定理这节课，能够更好地引导教学方向，促进高质量教学课堂的构建，提升学生几何直观能力，以下是几点教学思考.

1. 厘清五个教学阶段，使教学内容更具系统性、层次感

结合范希尔几何理论的五个教学阶段，教师能够充分把握教学进度，合理设计教学，如情境创设、“问题串”设计、自主探究活动等环节，这样既能够让教师在课堂教学中做到游刃有余，也能关注到学生的发展和探究能力的培养，促进教学质量的提升，真正做到在教学中教思考、教体验、教表达. 重视情境问题的创设，情境要贴合学生认知发展水平.设计“问题串”，能够激发学生的数学学习兴趣和求知欲. 在解决问题过程中，培养学生的独立思考能力，增强学生问题提出和解决的能力. 在新课程背景下，要求增加学生自主探究环节，旨在强调学生基于情境，独立解决问题，积累丰富的学习活动经验，在探究中习得关键的数学思想和方法. 基于范希尔几何理论设计教学内容，更具系统性、层次感. 一方面，教学知识规划更系统，对应范希尔几何理论的五个教学阶段来设计教学内容，使得教学时间分配和教学环节设计上更为合理. 另一方面，教学过程更具层次感. 知识学习应遵循循序渐进的原则，能够做到由浅到深、由简到繁，更好地满足学生的认知发展.

2. 有效结合信息技术，让教学更加生动直观

在正弦定理教学中，在探究各边与其对角正弦的比值中，适当借助几何画板，将常见的三种三角形的边与对角正弦值之比表示出来，学生通过观察图形变化，能够发现其比值始终是相等的，从而得出正弦定理，这样做不仅将复杂、抽象的内容具体化，而且能够加深学生对正弦定理的理解，帮助学生构建完整的、严谨的知识体系，在今后的正弦定理使用中，能够做到厘清知识误区，准确应用于实际解题中.

3. 以学生为主体，促进“三教”的生成

无论是情境问题的创设，还是教学中正弦定理证明的探索过程，都强调学生为主体的教学观，具体应从以下三点出发：一是要教会学生“思考”. 教学要做到“不愤不启，不悱不发”，目的是在严格要求学生的同时，适时启发诱导学生思考，给予学生足够的思考时间，让学生经历思考的过程，培养学生独立思考的能力. 二是要教会学生“体验”. 著名教育家杜威提倡“做中学”，目的就是要求学生在课堂中，通过经历实践活动，在探究问题的过程中，能够积累丰富的知识及活动经验，这样有助于构建较为系统的、完整的知识体系，对于学生后期学习是十分有益的.三是教会学生表达. 培养学生的表达能力并非一蹴而就，因此要落实到教学的各个环节中. 教学是师生、生生互动的过程，在教学问答中，要关注学生表达的方式和语言的准确性，适时纠正学生表达的误区. 在探究环节中，要倡导学生间的合作交流，积极营造良好的活动氛围，让每个学生都能参与其中，积极表述各自对问题的看法.

参考文献：

[1]  中华人民共和国教育部. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]  中华人民共和国教育部. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[3]  鲍建生，周超. 数学学习的心理基础与过程[M]. 上海：上海教育出版社，2009.