依托“阅读与思考”,提升数学味,凸显素养观

楼凌吉

[摘  要] “阅读与思考”汇集了数学知识的源起、发展、完善和应用，展示了古今中外的数学魅力，而在紧凑的进度下，其价值得不到充分的发挥，甚至沦为教材中的“边角料”. 文章以“圆锥曲线的光学性质及其应用”探究为例，在实践操作中发展直观想象素养，在探索求证中提升逻辑推理素养和数学运算素养，在实际生活问题的分析中提升数学抽象素养和数学建模素养. 研究者以为开展“阅读与思考”教学研究，可在数学文化中渗透数学思想和方法，隔离“数学畏”，提升“数学味”，激发学生学习数学的主观能动性，实现核心素养的螺旋式上升.

[关键词] 阅读与思考;数学文化;数学味;主观能动性;核心素养

[?]改善阅读现状，隔离“数学畏”

近几年，数学文化在高考试题中频频出现，不管是浙江卷的一小段，还是全国卷的大篇幅，只要看见文字材料，学生心里就充斥着“数学畏”. 学生堆积如山的书籍中，除了教材和教辅资料，基本见不着数学课外阅读书籍的身影;在网络平台上，学生为数学消耗的流量少之又少. 数学阅读意识和主动性的缺乏，究其根本是学生对数学的畏惧，甚至是抗拒. 同时，教师队伍中能被学生冠以“×神”的多半是数学教师. 看不见摸不着，却又时刻縈绕在心，有崇敬之意更有畏惧之心，在学生心中，神一样存在的不是数学教师，而是数学本身.

结合学生的认知发展，利用教材的每一板块，打磨教学的各个环节，研究如何将数学从“有畏”变成“有味”，数学教师责无旁贷. 在教学实践中，笔者发现“阅读与思考”在新授课阶段，往往因为进度问题被搁置，而到了高三复习阶段，随着教材成为压箱之物，其再次沦为“边角料”. 据初步了解，一线数学教师对“阅读与思考”进行深入研究的并不多，能和学生一起开展研究性学习的更是寥寥无几.

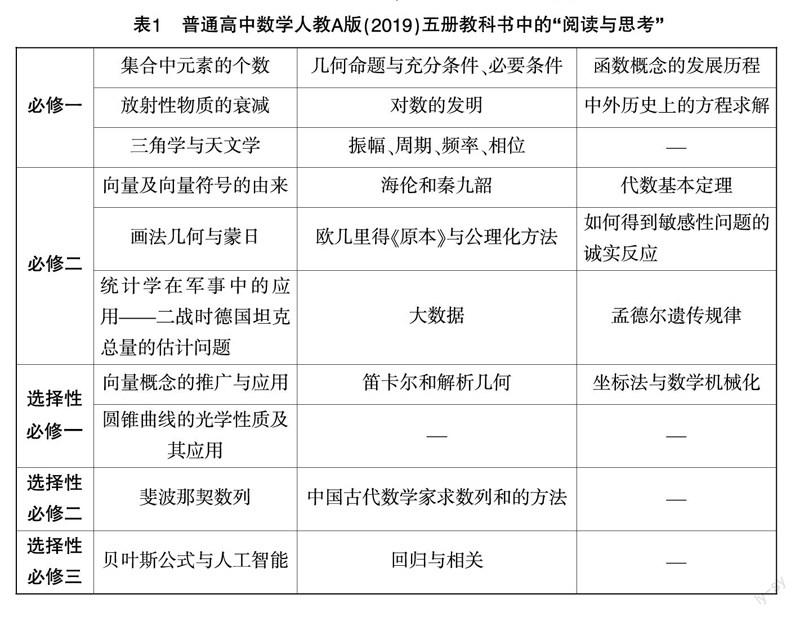
笔者罗列了普通高中数学人教A版（2019）五册教科书中的“阅读与思考”的标题（见表1），单从标题上看就足以刺激学生的味蕾. 它汇集了数学知识的源起、发展、完善和应用，展示了古今中外的数学魅力. 抽象的数学概念、巧妙的数学方法、深奥的数学思想，其起源和发展都是自然的，不仅合情合理，还富有人情味，这在情感上拉近了学生和数学的距离.

以下是笔者的一堂源于“阅读与思考”的探究性教学片段，展示它和大家一起感受“数学味”.

[?]“阅读与思考”教学案例分析——以“圆锥曲线的光学性质及其应用”为例

数学教学不只在于传授公式和定理，更在于激励学生从数学的角度去发现问题、思考问题、解决问题，进而建立数学学习自信心. 本节课通过创设具体生动的问题情境，点燃思维火花;类比圆的反射过程，经历观察、猜想、论证三部曲探究抛物线的光学性质;在互助合作中完成椭圆光学性质的探究;了解光学性质在生活中的应用，将理论上升到实践，感悟学习数学是有用的;以探究双曲线的光学性质为课后作业，进一步巩固解析几何的思想方法，体会圆锥曲线的统一性. 在教学过程中努力提升“数学味”，发展学生的核心素养，提升其独立获取数学知识的能力，增强学生学习数学的兴趣和学好数学的信心，培养其锲而不舍的钻研精神和科学态度.

1. 创设情境，引入课题

师：浙江省绍兴柯岩风景区的莲花听音景点是全国最大的石莲花，由99块巨石拼铺成半径为9.9米的圆形. 对着石莲花的是一堵圆弧形的回音壁，相传坐在莲花中心对着回音壁诵念经文可以和佛心共融共振. 我在游玩时对着回音壁说话，真的可以听到回音，但为什么只有站在莲花中央时，回音才是最明显的？

在回顾光的反射定律后，教师引导学生从情境问题中抽象出数学模型：从圆心射出的光线经圆反射后，反射光线再次经过圆心，基本解决开篇提出的问题.

师：大家只作出了入射光线和反射光线，请问法线在哪里？法线又是如何确定的？

在导数学习中，学生学习了用曲线上某点处的切线近似替代这一点附近的曲线，即“以直代曲”的思想方法. 在教师的引导下，学生能自然引进圆在入射点处的切线所在面作为反射面，再依次作出法线和反射光线.

师：回音有强弱之分能用图形来说明一下吗？

在交流合作中，产生了对照组（如图1所示），可以清晰地看到站在圆心A处能接收到更多的反射光波. 期间，教师要引导学生多做几组光线的反射，从A和B射出的光线，若只画一条经C处反射的光线，就无法解释回音的强弱. 因此，多次试验，仔细观察和认真分析可以找到一般规律. 积累从具体到抽象的活动经验，养成在日常生活中一般性思考问题的习惯，把握事物的本质，以简驭繁，运用数学抽象的思维方式思考并解决问题[1].

2. 精准作图，大胆猜想

类比圆中的光线反射问题，接下来研究从圆锥曲线的焦点射出的光线经曲线反射后的特点. 为使学生方便作图，教师在学案上印有精确的圆锥曲线，并标出焦点的位置. 同样，精确性也体现在学生的作图过程中，直尺是必需的，有量角器自然是极好的.

先从抛物线入手，学生依次作出入射光线、抛物线在入射点处的切线、法线和反射光线. 作完一条光线的反射线后，学生并没有发现当中蕴含的光学性质. 回顾上一环节，强调多次试验才能摸索出它们的共性，随后选取几张反射光线近乎平行的练习予以展示，最后将手动的探索过程转移到几何画板上，动态的演示使学生更加直观地感受到抛物线的光学特点，并大胆猜想：从焦点射出的光线，经抛物线上的一点反射后，反射光线平行于抛物线的对称轴.

3. 层层推进，分析论证

经历直观感受和大胆猜想，下一步就是分析论证. 如图2所示，从抛物线y2=2px的焦点F射出一条光线，经曲线上一点A（x，y）反射，求证反射光线平行于x轴.

要证明反射光线平行于x轴，即证明∠2=∠3，即证明∠1=∠3，即证明AF=BF.

因为抛物线y2=2px在点A（x，y）处的切线方程为yy=p（x+x），所以相应的法线方程为y-y=-（x-x），所以法线与x轴相交于点B（x+p，0），所以BF=x+=AF.

在证明过程中，学生进一步掌握了等价转化思想方法，巩固了抛物线的定义和在某点处的切线方程，经历了用代数方法解决几何问题的三部曲.

4. 明确结论，实践应用

通过上述的直观感受和分析论证，学生掌握了抛物线的光学性质. 在进一步介绍抛物面反射镜后，教师展示了2021年10月18日在希腊奥林匹亚的赫拉神庙前采集北京冬奥会火种的图片，并请学生思考其中的原理. 教材中还有许多抛物线光学性质的应用，这使学生感受到数学与生产生活的紧密关系.

5. 迁移方法，探究新知

以探究抛物线的光学性质为例题，椭圆的光学性质研究则是一个习题，通过“问题链”巩固研究椭圆光学性质的过程、方法和思想.

问题1：从椭圆的一个焦点射出的光线，经椭圆上的一点反射后，反射光线有什么特点？

问题2：怎么证明从椭圆的一个焦点射出的光线，经椭圆上的一点反射后，反射光线经过椭圆的另一个焦点？

问题3：如何利用椭圆的光学性质解释电影放映机的工作原理？

部分学生通过作图认为反射光线经过椭圆的中心，有学生马上提出异议：当选取椭圆的上顶点作为入射点时，反射光线经过另一个焦点. 得到此错误结论，究其原因，首先是作图不精确，其次是光线的条数过于单一. 精准作图，多次试验，结合特殊到一般的推理过程，不少学生能挖掘出椭圆的光学性质.

如图3所示，要证明法线AB为∠FAF的平分线，只要证明=.

因为椭圆+=1（a>b>0）在点（x0，y0）处的切线方程为+=1，所以相应的法线方程为y-y=（x-x0），所以法线与x轴相交于点B

x，0，所以==. 又

AF===x+a，同理

AF= -x+a，故=.

数学运算素养是最基本的素养，学生通过数学运算能力的发展，可以有效促进其数学思维的发展，进而养成科学严谨、求真务实的重要品质[2].

6. 课堂小结

通过把莲花听音中的回音问题抽象化、数学化，学生学会了光线反射到圆上的研究方法，并把它类比到圆锥曲线中，通过精准作图，大胆猜想，严格论证，发现了抛物线和椭圆的光学性质，了解了它们在实际生活中的应用，感受到了数学的强大“磁场”. 在研究过程中，要注重学生直观想象、逻辑推理、数学运算等核心素养的发展，在生活实际问题的分析中提升数学抽象素养和数学建模素养.

7. 教学反思

本节课提出了一些具有挑战性的问题，凸显了自主探究、合作交流等学习方式，部分学生并不能很好地适应，显得有些束手无策. 冰冻三尺，非一日之寒，这意味着教师在日常的课堂教学中还没有真正把主动权交给学生. 在有限的时间内，学生完成计算椭圆上的点到焦点的距离有一定的困难，可以先将教材中的“信息技术应用——用信息技术工具探索点的轨迹：椭圆”作为预备知识，了解圆锥曲线的第二定义，简化计算曲线上的点到焦点的距离，不仅为圆锥曲线光学性质的研究提供便捷，而且从离心率的角度再次体现圆锥曲线的统一性.

[?]依托“阅读与思考”，提升“数学味”，凸显素养观

学生经过中考分层，学习能力不相上下，并处于同一学习环境，而经过三年的时间，分差可以从中考的二十几分上升到几百分. 这期间，学生的主观能动性起着主导作用，能否主动、独立甚至富有创造性地学习不仅决定着他们的高考分高低，更决定着他们是否可以持续发展. 在现实生活、日常情境中，数学无处不在，常常日用而不自知，对数学模型的感知、判断、思考和应用，在一定程度上决定着我们的智性水平、理性高度和文野之分[3]. 数学教学切不可就题论题，停留在抽象的层面，否则极易引起学生的“数学畏”. “阅读与思考”给师生提供了教学素材，指明了教学方向，提升了“数学味”，凸显了素养观.

1. 数学可以追寻历史，放眼未来

数学是一面镜子，用数字、符号和图形折射出过去和未来. 在《放射性物质的衰减》中，引进良渚遗址中发掘的草裹泥来研究水坝的修建时间，进而刷新对中国文明起源的认知. 良渚古城被列入世界遗产，良渚文化得到国际社会的普遍认可离不开碳元素检测，它比其他史料和考古都更具说服力. 《放射性物质的衰减》文末还提出：如果函数呈指数增长，那么称函数值增长为原来的两倍所用的时间为“倍增期”. 将倍增期的概念和当下人口问题相结合，提出計算人口倍增期的两种方法：①p=pekn，②p=p（1+k）n，其中p为n年后的人数，p为原有人数，k为人口年增长率，n为经过的年数，当=2时，求得的n就是人口倍增期. 查阅过去几十年中国人口总数，经过函数拟合，预测20世纪80年代若无实行计划生育的情况下人口自然增长的倍增期，体会数学在国家宏观调控上的价值.

2. 数学可以洞察万物，精准反馈

数学是一部探测仪，可以强力分辨、准确定位隐埋在深处的问题. 《统计学在军事中的应用——二战时德国坦克总量的估计问题》介绍了用不放回抽样来估计离散型均匀分布最大值，强调统计方法的精确性和有效性是常规情报收集方法无法比拟的. 学习了《如何得到敏感性问题的诚实反应》，学生可以自己动手设计问卷，开展考试作弊、校园欺凌等敏感性问题的调查. 《孟德尔遗传规律》在概率统计的指引下开启了遗传学的大门，洞察到外在表象下隐含着的生命密码. 《大数据》依托数据和数据分析结果做出决策，影响着人们的生活方式，例如每天的天气预报. 近年来，教育事业快速发展，全面步入“智慧教育”新时代，其中一个方面就是大数据精准教学.

3. 数学可以化繁为简，高效运作

数学善于思考问题的共性，提出高效的解决方案，是计算机技术的基础和核心，是最强大脑. 《中国古代数学家求数列和的方法》介绍了北宋数学家沈括为了求一层层垒起的酒坛总数，提出了二阶等差数列的一个求和公式，即“隙积术”，为后续“垛积术”的研究奠定了基础. 学习《向量概念的推广与应用》，借鉴材料中校服厂家定制服装的过程，学生可以就班服的购买问题进行一次数学实战演练，选考技术的学生还可以根据所学的知识编写一套程序，高效解决这一问题. 这些“阅读与思考”可以让学生深刻地体会到数学在解决实际问题中的有效性.

[?]结语

“阅读与思考”的教学研究活动可以促使学生从实际背景抽象出数学问题，建立数学模型，运用数学语言表达问题，用逻辑推理解决问题，进一步指导实践，极大地活跃学生的数学思维. “阅读与思考”的课堂富有问题性、抽象性、推理性、探索性，充满着“数学味”. 高中数学教学以发展学生的核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质[4]. 数学虽源于对现实世界的抽象，但在教学过程中不能只有抽象，还应时时刻刻回顾其与社会生活的关系，为社会创造的价值. “阅读与思考”真正体现了这一要求. 因此教师应将“阅读与思考”教学落到实处，提升“数学味”，凸显素养观，充分发挥学生的主观能动性，使学生以更高的热情投身于数学学习.

参考文献：

[1]  中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.

[2]  王娟，李保臻. 基于数学运算能力培养的单元教学设计研究——以初中“因式分解”内容为例[J]. 中学数学教学，2019（04）：1-6.

[3]  裴亚光. 数学教学是圆梦之旅——在湖北大学第四届（2017）数学文化节上的报告[J]. 中学数学教学参考，2019（25）：2-4.

[4]  中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.