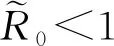一类具有非线性发生率的随机SIRS传染病模型的动力学行为

热木孜亚·热布哈提，王春霞

(新疆医科大学医学工程技术学院，新疆 乌鲁木齐 830017)

传染病的流行给人类健康和社会发展造成巨大影响，因此，传染病的预防与控制研究吸引了大量学者，研究者运用数学建模研究其传播规律，以达到通过人为干预来切断疾病的传播途径，从而达到控制疾病传播的目的.

众所周知，随机噪声因素在传染病的传播中起着重要作用，因此，许多学者对传染病模型随机性的影响进行了研究[1-8]，不同的随机干扰方法被引入到传染病模型中.但是，仍然有许多重要的问题并没有充分的研究，如具有一般非线性发生率的随机传染病模型.到目前为止，只有一些非线性发生率的特殊情况，如饱和发生率被考虑，但是，数学流行病学理论中非线性发病率是非常重要的.因此，开展具有一般发生率的随机传染病模型的研究是具有重要意义的工作.

本文考虑具有一般非线性传染率的随机SIRS传染病模型

dS(t)=(Λ-μS-βf(S，I)+δR)dt-σf(S，I)dB(t)，dI(t)=(βf(S，I)-(μ+γ+α)I)dt+σf(S，I)dB(t)，dR(t)=(γI-(μ+δ)R)dt，

(1)

其中：S(t)、I(t)和R(t) 分别表示t时刻易感者、染病者和恢复健康者的人数；Λ表示人口输入率；μ是S、I和R的自然死亡率；δ是免疫丧失率系数；γ是恢复率系数；α是因病死亡率.疾病的传播受非线性发生率βf(S，I)的影响，其中β是S和I间的接触率系数.在本文中，假定δ和α是非负常数，且Λ、μ、β、γ都是正常数.模型(1) 是由以下相应的确定性模型构造的：

S′(t)=Λ-μS-βf(S，I)+δR，
I′(t) =βf(S，I)-(μ+γ+α)I，
R′(t) =γI-(μ+δ)R.

(2)

1 预备知识

对于模型(1) 中的函数f(S，I)，我们引入以下假设：

根据模型(1)的依概率1全局正解的存在性、唯一性和最终有界性，我们得到如下结果：

引理1可以用类似于文献[3]中的方法证明.

注2定义

Γ={(S，I，R)：S>0，I>0，R>0，S0≤S+I+R≤S0a.s.}.

根据引理 1，Γ是模型(1)的依概率1正不变集.

2 无病平衡点的全局渐近稳定性

显然，模型 (1) 存在唯一的无病平衡点E0=(S0，0，0).对于模型(1)，定义

定理1假设条件(H)成立.如果下面条件之一成立，则无病平衡点E0全局渐近稳定：

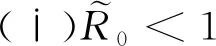
证明：令(S(t)，I(t)，R(t))是模型(1)的任意解，且对任意的t≥0，有(S(t)，I(t)，R(t))∈Γa.s..显然

I(t)≤S0-S(t)， 对任意的t≥0，

(3)

并且当常数n2≤2时，有

(4)

此外，对任意常数ρ>0和任意的0≤I，S≤S0，又有

(5)

现在定义如下Liapunov函数

其中n1和n2是正常数，V(S，I，R)在区域Γ内是正定的.计算LV(S，I，R)，有

由式(3)～(5)和(H)，进一步有

(6)

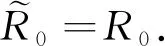
当σ2>β2/2(μ+γ+α)时，有

因此，如果条件(ⅰ)成立，则从式(6)进一步可得

(7)

如果条件(ⅱ)成立，则从式(6)进一步可得

(8)

首先取常数ρ>0，使得

接下来取充分小的常数n1>0和n2>0，使得

则由式 (7)和(8)，最终可得LV在区域Γ内负定.因此，根据文献[9-10]关于依概率1全局渐近稳定性的定理，我们可得E0的全局渐近稳定性.证毕.

3 疾病的平均持久性

对于定义在t∈+0上的函数u(t)，我们定义函数u(t) 在区间[0，t]上的平均值

关于模型(1) 疾病的平均持久性我们有如下结果：

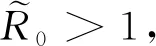
证明：令(S(t)，I(t)，R(t))是模型 (1) 的任意解，且对所有的t≥0有(S(t)，I(t)，R(t))∈Γa.s..对模型 (1) 的两边从0 到t积分并除以t，可得

所以有

因此

(9)

其中

由引理 1，显然有

根据拉格朗日中值定理，当t≥0时，进一步得

其中ξ(t)∈(S(t)，S0)，ζ(t)∈(0，I(t)).由

有

-

因此，当t≥0时，可得

对任意的t≥0，对上面的不等式两边从0 到t积分并除以t，可得

(10)

将式 (9) 代入式 (10)，得

令

M(t)是一个连续局部鞅且M(0)=0.由假设条件(H)知，二次变分满足

得

进一步有

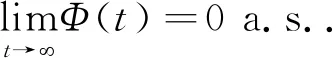
综上可得(参见文献[10])

其中

因此，取t→，最终可得

最后，从模型 (1) 的第3个方程，很容易得到

证毕.

4 数值模拟

在模型(1)中，取f(S，I)=f(S)g(I)，其中f(S)=S，g(I)=I/(1+ωI).

图1满足初值(S(0)，I(0)，R(0))=(0.5，0.6，0.6)，σ=0.85Δt=0.001的随机模型(1)和相应的确定性模型(2)的S(t)，I(t)，R(t)的轨迹Fig.1Paths S(t)，I(t)，R(t) for stochastic system (1) and corresponding deterministic system (2) with initial value (S(0)，I(0)，R(0))=(0.5，0.6，0.6)，σ=0.85 and step size Δt=0.001

图2满足初值(S(0)，I(0)，R(0))=(0.5，0.6，0.6)，σ=0.9 Δt=0.001 的随机模型(1) 和相应的确定性模型(2) 的S(t)，I(t)，R(t)的轨迹Fig.2Paths S(t)，I(t)，R(t) for stochastic system (1) and corresponding deterministic system (2) with initial value (S(0)，I(0)，R(0))=(0.5，0.6，0.6)，σ=0.9 and step size Δt=0.001

5 结 论

本文研究了一类具有非线性发生率的随机SIRS传染病模型的动力学行为.我们在这里定义了新的阈值(该阈值与相应的确定性模型的基本再生数R0不同)，建立了无病平衡点全局稳定性、疾病平均持续性的阈值判别准则.