一类求解大规模非线性单调方程组的无导数共轭梯度方法

李艳冉，高 静，曹名圆，姜晓威，白 雪

(北华大学数学与统计学院，吉林 吉林 132013)

本文考虑非线性单调方程组

F(x)=0，

(1)

其中F(x)：n→n单调且连续，即F(x)满足对∀x，y∈n，有(F(x)-F(y))T(x-y)≥0.非线性单调方程组广泛应用于图像分割[1]、电力系统的操作与控制[2]、信号重构[3]等众多领域.数学领域中的有序回归问题[4]、单调变分不等式问题[5]以及具有Bregman距离的广义近端算法的子问题[6]也可以转化为非线性单调方程组来求解.牛顿法、拟牛顿法等经典求解算法由于每步迭代过程中都需要计算雅克比矩阵或者雅可比矩阵的近似矩阵，不适合求解大规模方程组，因此，当问题规模很大时，很多学者更倾向于使用结构简便、存储空间小的共轭梯度法来求解大规模非线性单调方程组问题.

minf(x)，

其中，f：n→是光滑函数.假设xk是第k步的迭代点，dk是搜索方向，αk是步长，gk是f(x)在点xk处的梯度，βk为共轭参数，则第k+1步迭代点的选取格式为

xk+1=xk+αkdk，k=0，1，2，…，

不同的βk对应不同的共轭梯度法，常用的共轭参数有

2012年，Rivaie等[7]提出了RMIL共轭梯度法求解无约束优化问题，其共轭参数βk定义为

该算法的数值结果表明，RMIL共轭梯度法与其他共轭梯度法相比，在运算性能方面更占优势.2020年，Fang[8]在此基础上，提出了一类求解非线性单调方程组的改进的RMIL无导数共轭梯度法，在RMIL共轭参数的基础上引入了谱参数θk，使

该方向dk无需步长αk的调节即可满足充分下降性.

当确定搜索方向dk后，通过线搜索技术找到点

zk=xk+αkdk，

使其满足

(F(zk)，xk-zk)>0.

另一方面，对于满足F(x*)=0的任意x*∈，根据F的单调性，可得

(F(zk)，x*-zk)=-(F(x*)-F(zk)，x*-zk)≤0.

因此存在超平面

Hk={x∈n(F(zk)，x-zk)=0}，

将单调方程组(1)的解x*从xk中严格分开.基于上述结论，文献[8]中将xk投影到Hk上得到下一迭代点xk+1：

(2)

该投影技术结合无导数线搜索技术确保了搜索方向的有界性和算法的全局收敛性.数值实验表明，在求解大规模非线性单调方程组问题时，该方法优于同类算法.

2019年，Liu和Feng[9]提出一类求解带有凸约束的非线性单调方程组的无导数共轭梯度法，将DY共轭参数改进为

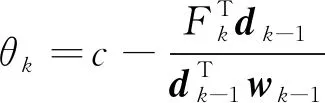
受上述文献的启发，本文提出了一类求解非线性单调方程组问题的无导数共轭梯度法，改进共轭参数βRMIL，利用不等式证明技巧，构造与之对应的谱参数θk，使搜索方向dk满足充分下降性和有界性，进而证明算法的整体收敛性.

1 算 法

算法1

步0 选取初始点x0∈n，令δ>0，σ>0，s>0，ε>0，1>ρ>0，kmax>0，α=s，d0=-F(x0).并令k=0.

步2 若α满足

(3)

步4 计算F(xk+1)，yk=F(xk+1)-F(xk).确定搜索方向

(4)

其中γ∈(0，1)，yk=Fk+1-Fk，wk=dk+tkyk，

(5)

现在，我们证明由式(4)和(5)确定的搜索方向dk满足充分下降性条件.

引理1设dk由算法1产生，则dk满足充分下降性条件，即

2 收敛性分析

为了得到算法1的整体收敛性证明，现在给出如下假设.

假设1(ⅰ)非线性单调方程组F(x)=0的解集是非空的.

(6)

假设1表明，存在正数κ，对∀x∈n满足

(7)

引理2若假设1成立，且{xk}由算法1产生，则对任意的x*满足F(x*)=0，有

此外，{xk}满足

(8)

具体证明参见文献[8].

引理3若假设1成立，且{xk}、{dk}由算法1产生，则有

其中，κ、γ、s、L均为常数，并且κ>0，1>γ>0，s>0，L>0.

证明：由式(2)和算法1的步2可知

(9)

又根据算法1步2中线性搜索的定义以及αk是{s，ρs，ρ2s，…}中使式(3)成立的最大数，1>ρ>0可知

αk≤s.

(10)

(11)

综上，由式(6)～(7)和(9)～(11)可得

证毕.

引理4若假设1成立，xk、αk、dk、Fk由算法1产生，对所有k∈，存在常数ε，满足Fk≥ε，则有

具体证明参见文献[8].

综合以上结论，可以获得算法1的整体收敛性定理.

定理1若假设1成立，且{xk}，{dk}由算法1产生，则有

(12)

另外，序列{xk}收敛到x*且F(x*)=0.

证明：假设式(12)不成立，则存在常数ε>0满足

(13)

根据引理1可得

(14)

因此，由式(13)和(14)可知

(15)

(16)

由式(8)、(9)和(16)可得

(17)

另一方面，结合引理4和式(15)，有

此式与式(17)矛盾，进而表明式(12)成立.由假设1和引理2以及式(12)，能够推出{xk}收敛到x*，且x*满足F(x*)=0.证毕.

3 数值实验

将本文算法1与文献[8，10]提出的MRMIL1和DFPB1算法进行比较.本文所有数值实验都是在4 GB内存Intel CPU I5-4210的PC机上，用Matlab R2015b 编程完成的.

本文利用文献[11]中定义的分式

刻画算法性能.这里，P是测试集，|P|是测试集P中问题的数量，V是符合条件的问题集，tp，ν表示计算机运算测试问题所花费的CPU时间，或者函数调用次数，或者函数迭代次数.

图1给出了本文算法1(黑色实线)与MRMIL1(绿色实线)和DFPB1算法(红色实线)在CPU时间、函数调用次数和函数迭代次数方面的实验结果对比.图1的横坐标τ表示一种算法求解测试问题的最快(高)效率的百分比，纵坐标ρv(τ)表示每种方法成功解决的测试问题数量的百分比.从图1 a和图1 b中可以看出，在函数调用次数和CPU时间方面，算法1的性能曲线在其他两条曲线之上，说明本文提出的无导数改进RMIL共轭梯度方法在求解大规模非线性单调方程组问题时能够使用更少的函数调用次数和CPU时间，求解效率更高.因此，从函数调用次数和CPU时间方面考虑数值性能，本文算法明显优于文献[8，10]中的方法.图1 c显示的是算法迭代次数的对比结果，从图像可以看出，当τ<2时，算法1与DFPB1算法的数值表现基本一致，稍逊于MRMIL1；当τ≥2时，三个算法在迭代次数方面表现相当.

图1算法性能对比Fig.1Comparison of algorithm performance

4 小 结

本文主要研究了求解大规模非线性单调方程组的高效算法，提出了一类基于投影技术的无导数共轭梯度方法.证明了搜索方向满足充分下降性条件，在无导数线搜索和适当假设条件下，证明了算法的整体收敛性.数值结果表明，该算法在求解大规模非线性单调方程组时具有较高效率，在函数调用次数和CPU时间方面的表现优于同类算法.