几种类周期函数处理方法
黄石市第七中学(435000) 谷文俊
武汉第十一中学(430000) 凌才元
周期性是函数的重要性质,也是高考的高频考点之一.有些题目中会碰到在解析式或图像特征与周期函数类似的函数,我们称之为类周期函数,对这类函数问题的解决比周期函数难度大.本文总结了几种类周期函数的一些处理方法与大家一起探讨.
一、f(x+T)=f(x)+m 类线性型
(一)周期原理
1.若函数g(x)是以T为周期的函数,则f(x)=g(x)+ax+b为该类型的类周期函数.即周期函数加上一次函数构成的新函数为类周期函数.其中周期函数的周期T为类周期函数的周期.
证明f(x+T)=g(x+T)+a(x+T)+b=g(x)+ax+aT+b,则f(x+T)=f(x)+aT且直线的斜率为.
注一次函数可以看做周期为任意实数的类周期函数.
2.若函数f(x),g(x)是以T1,T2为周期的类周期函数,则f(x)+g(x)也是类周期函数,且周期为T1,T2的最小公倍数.
证明令h(x)=f(x)+g(x),T=k1T1,T=k2T2.
由题可知:f(x+T1)=f(x)+m1,g(x+T2)=g(x)+m2.所以,h(x+T)=f(x+k1T1)+g(x+k2T2)=f(x)+g(x)+k1m1+k2m2.
(二)函数图像变化与特征
首先观察两个函数图像:
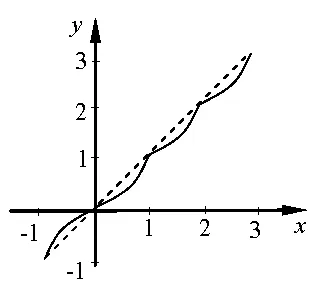
图1
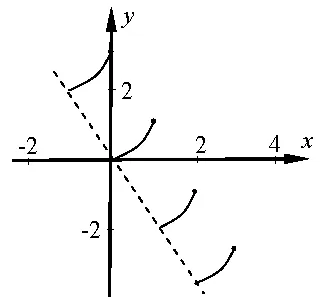
图2
(1)若f(x)为奇函数,当x>0 时f(x+1)=f(x)+1,若0 ≤x≤1 时f(x)=x2则f(x)图像为图1.
(2)定义在R 上的函数f(x)满足:f(x+1)=f(x)-2,若0 ≤x <1 时f(x)=x2,则f(x)图像为图2.
1 函数图像沿着某直线展开
上面两图函数图像分别沿着y=x,y=-2x展开.类比可知,满足f(x+T)=f(x)+m关系的类周期函数图像沿着斜率为的直线展开.即满足f(x)=g(x)+ax+b的类周期函数图像沿直线y=ax+b展开.
2 函数图像以周期为单位平移(T>0)
类周期函数图像从左至右以周期为单位,后一个周期的图像在前一个周期的基础上向上(m>0)平移或向下(m <0)平移|m|个单位.
(三)对称性
1.若函数f(x),g(x)是均以T为周期的类周期函数,且函数f(x)关于(x0,y1)对称,函数g(x)关于(x0,y2)对称,则f(x)+g(x)关于(x0,y1+y2)对称.
证明由对称可知:f(x)+f(2x0-x)=2y1,g(x)+g(2x0-x)=2y2,令h(x)=f(x)+g(x),则h(x)+h(2x0-x)=f(x)+g(x)+f(2x0-x)+g(2x0-x)=2(y1+y2).证毕.
2.f(x)=sin(wx+θ)+ax+b类型函数对称性的探讨

例1设g(x)定义在R 上以1 为周期的周期函数,若f(x)=g(x)+x在[3,4]上值域为[-2,5],则f(x)在[-10,10]上的值域.
分析由题可得:f(x+1)=f(x)+1,则f(x)以1为周期的类周期函数.当x ∈[9,10]时,x -6∈[3,4],则f(x)=f(x -6)+6∈[4,11],当x ∈[-10,-9]时,x+13∈[3,4],则f(x)=f(x+13)-13∈[-15,-8].所以f(x)∈[-15,11].
例2函数的图象大致是()
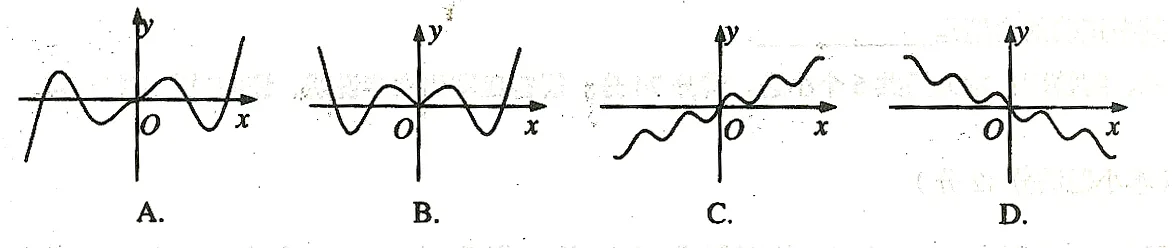

二、f(x+T)=kf(x)(T>0,k>0)类指数型

分析由题可得函数部分图像如图3.设x ∈(2,3]则x - 2 ∈ (0,1],f(x)=2f(x - 1)=4f(x - 2)=4x2-20x+24.令则.或观察图像可得正确答案为选项B.
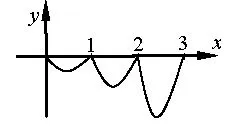
图3
三、f(kx)=nf(x)(k>1)类幂指型
这种类型的类周期函数它的周期不断变化,从左至右类周期成以k 为公比等比数列变化.图像从左至右每个周期内的最值(且不为0)以n 为公比成等比数列.


