2019年高考数学史试题分类评析与教学建议

首都师范大学数学科学学院(100048) 覃淋

1 引言

近年来,随着对数学的本质认识的不断深化,不管是数学家或是数学教育工作者,都越来越认同“数学是人类文化的重要组成部分”.《普通高中数学课程标准(2017)》从基本理念、课程目标、实施建议等方面对“数学文化”作了明确要求,强调要将数学文化融入数学教学中.通过在数学教学活动中渗透数学文化,让学生了解数学的发展历程,认识数学在科学技术和人类社会发展中的所起的重要作用,引导学生认识和感悟数学的文化价值,提升人文素养及数学核心素养[1].

考查近年来的高考试卷,可以发现每套试题都在有意识地渗透数学文化,主要体现在数学史、数学精神和数学应用三个方面[2].以数学文化作为试题背景已成为高考命题的新亮点和新趋势.数学文化作为数学的重要组成部分,对学生数学核心素养的培养起着重要作用.这类试题具有其它一般数学试题难以比拟的文化价值、教育价值以及科学价值,数学文化试题的意义和价值超越了试题本身.比如:2017年全国卷II 理科第3 题以我国明代程大位的数学著作《算法统宗》中的古算诗题为素材考查等比数列求和公式,2018年全国卷I 理科第10 题以“希波克拉底定理”为背景考查几何概型,2019年全国卷III 文理科第21 题和浙江卷第21 题都以阿基米德《方法论》中的相关命题为背景考查解析几何的相关内容.

数学史作为数学文化的重要组成部分,对学生的数学核心素养的培养起着重要作用.高考作为指挥棒,将数学史融入高考数学试题能进一步发挥其育人的功能.数学史作为高考数学试题的命题背景,主要包括数学家生平、数学史上的标志性事件、数学名著、数学名题、数学符号、数学公式、数学图形以及数学史上论争等.本文对2019年全国13 套(文、理科)高考数学试卷中数学史试题进行分类、统计,对命题特点进行分析.一方面为以后高考命题者编制出素材更加丰富、题型更加新颖的试题提供启发;另一方面,为教师更合理地使用教材中的数学史料进行教学提供可借鉴的方法.

2 高考数学史试题评析

2019年全国共13 套高考数学试卷:全国卷I(文理)、全国卷II(文理)、全国卷III(文理)、北京卷(文理)、天津卷(文理)、浙江卷、江苏卷和上海卷.对13 套试题中的数学史试题进行统计,6 道数学史试题的基本情况如表1所示.

表1:2019年高考试卷中的数学史试题

13 套试卷中共有6 道数学史试题,其中全国卷I、全国卷III、浙江卷各两道,北京卷、上海卷、全国卷II、江苏卷和天津卷均没有.可以发现:第一,从题型看,题目类型丰富,有选择题、解答题和证明题;第二,从史料涉及领域看,涉及了代数、不等式、解析几何、立体几何和概率等;第三,从史料涉及内容看,包括黄金分割、均值不等式、阿基米德方法论、柯西不等式、祖暅原理等数学史.

13 套试卷中的数学史试题的命题来源有三种:(1)以数学史上著名问题或定理为背景;(2)以中国古代数学家的研究成果为背景;(3)以国外数学家的研究成果为背景.下面分别来说明.

2.1 以数学史上著名问题或定理为背景

评析2019年6月7日数学考试结束不久,此题便引发了广泛讨论.此题以古希腊毕达哥拉斯学派提出的黄金分割为背景设置题目,出乎广大考生和教师的意料之外.此题以著名雕塑“断臂维纳斯”为载体,探讨人体黄金分割之美,将美育融入数学教育之中,很好地将数学与其它学科联系起来了.

“将已知线段分割为两部分,使其中一部分是全线段与另一部分的比例中项.”就是所谓的黄金分割问题,这种分割有许多不同的名称.通常称之为“黄金分割(golded section)”,又称为“中外比”、“中末比”.黄金分割和正五边形、正十边形以及五角星的作图有着密切关系.“黄金分割”很有可能起源于毕达哥拉斯学派研究正五边形的作图.关于中末比的系统研究,最早的可能是古希腊数学家欧多克斯(Eudoxus,约公元前400—前347).

黄金分割这一名称出现很晚.意大利数学家帕乔利(Luca Pacioli,1445-1517)在其著作《神圣比例》(1509)中将中末比称为“神圣比例”;天文学家开普勒(Johannes Kepler,1571-1630)在《宇宙之谜》(1596)中称中末比为比例分割.最早在书中使用黄金分割名称的是欧姆(Martin Ohm,1792-1872),在《纯粹初等数学》第二版(1835)中使用了“goldene Schnitt(黄金分割)”.19世纪之后,黄金分割这一名称逐渐通行.

关于黄金分割的系统论述,最早见于《几何原本》.《原本》卷II 第11 题[3]:分已知线段为两部分,使全线段与一小段构成的矩形等于另一小线段上的正方形;卷IV 第10 题,卷VI 第30 题,卷XIII 第9 题都提到了黄金分割问题.

评析此题的命题背景包括均值不等式和柯西不等式.不等式主要研究数的不等关系,与数、式、方程、函数、数列以及三角等数学内容有非常密切的关系,不等式的证明历来也是高考的一个重点.

均值不等式有着非常悠久的历史,可以追溯到古希腊毕达哥拉斯学派,毕达哥拉斯学派研究过多种比例中项,但他们没有讨论这些数之间的大小关系.阿基米德在《论球与柱体》中,在证明球的体积公式时,利用了如下结果:设α,β 是两条已知线段,并且α＞β.在α 和β 之间插入两条为等差中项的线段δ 和ε(即α,δ,ε,β 构成等差数列),那么α3:δ3＜α:β.但没有给出证明.

公元3世纪末,帕普斯(Pappus)在《数学汇编》中给出了图1,利用此图即可得到.

图1

2.2 以中国古代数学家的研究成果为背景

例3.(浙江卷第4 题)祖暅是我国南北朝时期的伟大的科学家,他提出“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h 是柱体的高.若某柱体的三视图如右图所示(单位:cm),则该柱体的体积(单位:cm3)是()

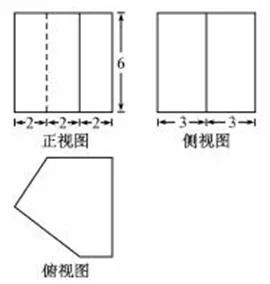
图2

A.158 B.162 C.182 D.324

评析此题以南北朝大数学家祖暅(456-536)提出的“祖暅原理”为背景,考查由三视图求面积、体积,考查直观想象、逻辑推理等数学学科核心素养.本题的关键是由三视图还原几何体,是一道容易题.

祖暅是我国古代伟大的数学家、天文学家.他在刘徽提出的“牟合方盖”的基础上,提出了祖暅原理,求出“牟合方盖”的体积,推导出了球的体积公式.关于祖暅认真刻苦学习的事迹,《南史·祖冲之传》中有记载:“……入神之妙,般、倕无以过也.当其诣微之时,雷霆不能入.”

祖暅所取得的成就,并不是轻轻松松就得到的,而是长期思考,不断学习,站在巨人的肩膀上取得的.在教学中,通过对某些数学公式、定理、符号的历史的介绍,可以激发学习动机,展现数学人文性的一面,使数学不那么可怕,培养学生积极的情感态度和价值观;了解数学家在创造数学的经历的曲折过程和错误,知道并非只有自己在数学学习上有困难而感到有所安慰;帮助学生理解数学在社会中的作用等等.让他们知道,数学作为人类的一项活动,是不断向前发展的,并不是一出现就具有像教科书中那种完美的形式,而是一代又一代数学家艰苦奋斗的结果.

题目对祖暅取得的成就的介绍,体现了习总书记所强调的文化自信,可以在潜移默化中增强学生的民族自豪感.这种处理方式和2018年全国卷II理科卷第8 题是一样的.实际上,把前面介绍“祖暅原理”的内容去掉,把题目改为“若某柱体的三视图如右图所示,则该柱体的体积是多少? ”也不会影响学生解题,这里题目以附加的形式运用数学史,史料内容可以与题目分离[4].

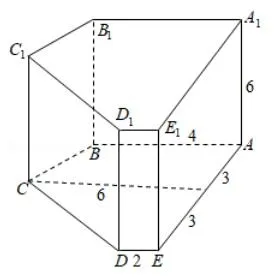
图3

2.3 以国外数学家的研究成果为背景

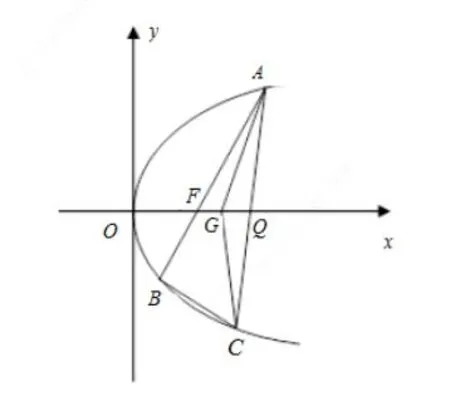
图4

例5(浙江卷第21 题)如图4,已知点F(1,0)为抛物线y2=2px(p＞0)的焦点,过点F 的直线交抛物线于A,B 两点,点C 在抛物线上,使得ΔABC 的重心G在x 轴上,直线AC 交x 轴于点Q,且Q 在点F 的右侧.记ΔAFG,ΔCQG 的面积分别为S1,S1.

(I)求p 的值及抛物线的标准方程;

评析这两题以阿基米德的《方法论》(The Method of Archimedes)和《求抛物弓形的体积》(Quadrature of the Parabola)中的相关内容为背景,进行改编重构,设置题目.考查抛物线、直线方程、重心性质、函数最值、弦长公式以及三角形面积等基础知识,综合地考查了学生分析和解决问题的能力.同时考查数学建模、逻辑推理等数学学科核心素养.属于中档题.

实际上,考查历年的高考数学试题,可以发现《方法论》中的“抛物弓形面积”是一个命题热点,几乎每年都有以此为背景的考题.如江西卷22 题(2005),全国卷II 21 题(2006),江苏理科19 题(2007),山东卷22 题(2008),江西卷21 题(2008),辽宁卷20 题(2013),浙江卷21 题(2018),浙江卷21题(2019).从题型上来看,均为解答题,属于中等难度.而且,在教材上有与此类似的题目,人教A 版选修2-1 第二章“圆锥曲线与方程”的复习参考题B 组第3 题:如图5,已知直线与抛物线y2=2px(p＞0)交于A,B 两点,且OA⊥OB,OD⊥AB 交AB 于点D,点D 的坐标为(2,1),求p 的值.

图5

高考数学试题的命制来源于教材又高于教材,这也为我们高三复习指明了方向——要关注教材,要重视教材,不要搞题海战术.今年的高考题和往年相比,大变样,没有按套路出牌,使得很多学生和老师觉得题目“很难”.这对那些背死书、走套路的学生来说,是比较难.

实际上,很往年相比,数学试题的难度反而降低了.虽然难度降低了,却更灵活了,要求也更高了.正如李尚志教授所说:“考题灵活,将ABCD 的汤换成维纳斯的头和脚这样的汤,把死记硬背的考生打蒙,把他们入学的门关窄一点甚至关死,让他们除了吐槽晕倒和哭泣之外无计可施,让那些潜心学习的考生不需要那么高的考分就能进大学.”这也会是今后高考改革坚持的方向:从能力立意到素养导向转变,突出学科核心素养,以数学知识为载体,将基础性和创新性作为考查重点,考查学生识别、分析和解决问题的能力.

这里试题背景是《方法论》中的命题1:抛物弓形的面积是其内接三角形面积的4/3.《方法论》中有15 个命题,包含阿基米德计算许多图形的面积和体积的方法、技巧等,阿基米德特别声明这并不是严格证明[5]:“这些定理将来必须用几何方法加以证明,因为以上方法不算真正意义上的证明.”而后在《求抛物弓形的体积》中给出了抛物弓形面积结果的几何证明.证明思想是利用欧多克斯的穷竭法,即在弓形内部作一系列的多边形去逼近弓形,使弓形的面积与内接多边形的面积之差小于任一给定值,再用归谬法证明.这里试题背景的意义与价值已超出了试题本身,将数学的理性精神表现得淋漓尽致.

例6(全国卷III 文理科第23 题)设x,y,z ∈R,且满足x+y+z=1.证明:

(I)求(x-1)2+(y+1)2+(z+1)2的最小值;

评析此题的命题背景是柯西不等式,柯西不等式最初由柯西提出(1821),该不等式的积分形式是布尼亚科夫斯基在1859年提出的,施瓦茨在1888年给出了该不等式的积分形式的证明.柯西不等式有许多形式,如向量形式、三角形式、概率论形式、积分形式等,在许多数学分支有着广泛的应用.是高考数学命题和数学竞赛命题的热点,如2013年湖南卷理科第10 题,2014年福建卷理科第21 题,2019年全国卷I 第23 题.人教A 版选修4-5 中介绍了柯西不等式.

试题解法(I)由柯西不等式,有

3 结论与建议

从数学史在2019年高考数学试题中出现的次数及史料内容看,可以发现命题者都比较重视将数学史融入到试题中,融入方式也变得多种多样,改变了以往单纯的知识性考查.不管是从学生学习的角度看,还是从教师教学的角度看,或是数学本身而言,数学史都是非常重要的,因为“一门科学的历史就是这门科学本身”.为了使高考试题中的数学史内容更加丰富,更好地体现数学史的教育价值和文化价值,试卷中数学史试题的数量、史料内容的选择都有待改进.

第一,增加试卷中数学史试题的数量.从前面的统计可以看到,2019年全国共有13 套高考数学试卷,仅有6 道数学史试题.其中全国卷I、全国卷III、浙江卷各两道,北京卷、上海卷、全国卷II、江苏卷和天津卷均没有.从这一点来说,命题者对数学史的重视程度还不够.因此,可以考虑适当增加试卷中数学史试题的数量,在高考试题中融入数学史,可以引导中学数学的教学.HPM 的教学实践研究表明,数学史可以激发学生的学习兴趣、增加学习动机、帮助学生理解重要的数学概念等教育价值.通过数学史的介绍,一方面可以激发学生的学习兴趣,增强学习数学的信心;另一方面,数学史展现了数学知识发生和发展的过程,可以帮助学生进一步理解概念[6].

第二,进一步加强不同学科之间的联系.从上面的统计结果可以看到,6 道试题仅有1 道试题涉及了数学与其它学科之间的联系.全国卷I 中的人体黄金分割很好地将美学与数学结合在一起,体现了美学中的数学.实际上,数学的思想和方法已经渗透到社会的方方面面,涉及到整个自然科学、社会科学、工程计算、管理、经济和文学领域.因此,在试题命制时,可以考虑将数学与物理、生物、历史、音乐、体育、文学、哲学等学科联系起来,使得不同学科之间的知识成为一个整体,这样可以促进学生更有效地学习数学.

第三,高考数学的复习应重视教材.由以上分析知,6 道数学史试题中,有2 道试题涉及均值不等式和柯西不等式,有2 道试题涉及阿基米德《方法论》和《求抛物弓形的面积》,还有一道试题涉及了祖暅原理.实际上,这里的6 道数学史试题中,除了全国卷I 黄金分割那道试题外,其余5 道试题所涉及的数学史在教材中都有体现,这一方面说明了高考试题来源于教材,高于教材;另一方面也为高三复习指明了方向.