探究问题模型 实现多题一解——用平移齐次化的方法处理全国I卷中一类解析几何问题

广州市执信中学(510080) 朱清波

近4年的全国I 卷解析几何试题中,2017年、2018年、2020年这3年的考查方向均为椭圆中定点定值问题,所不同的是前两年题干所给条件(或结论)是与“斜率之积”或“斜率之和”直接相关,而2020年试题的方向是利用所给条件进行验证式证明.这类问题的常规解答思路一般为:设直线方程为y=kx+b,再将直线所满足的条件最终转化为参数k,b之间的线性关系,最终判断该定点坐标(当然也需要考虑直线斜率是否存在的情况).在求解过程中韦达定理的正确形式和斜率之和或积为定值的合理转化是能否顺利解出答案的两个最重要的因素,但该思路运算量往往较大,大量考生往往出现会算但算不对或算不全的现象.如何另辟蹊径找到减少计算量的方法或把它们统一转化到熟知的常规模型,是一个值得探究的问题.以下从3 道高考真题来开展一种相对特殊的解法探究,以期对这类问题有更高层次的认知.

(1)求C的方程;

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.

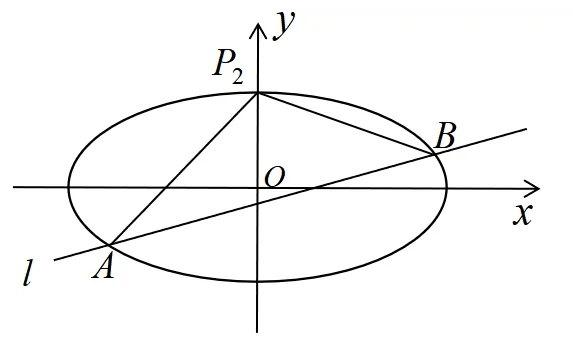
图1

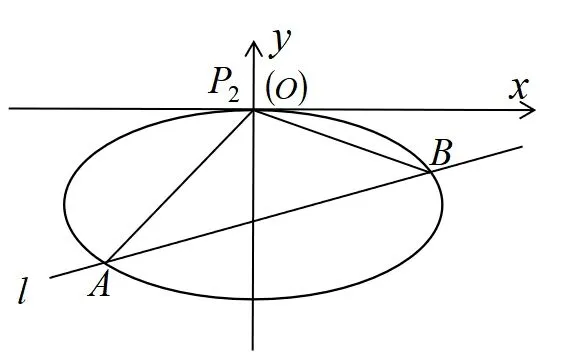
图2

图3

图4

图4,将椭圆E:x2+9y2=9 和直线CD沿n=(-3,0)平移变换,得到曲线E2:(x+3)2+9y2=9,即x2+9y2+6x=0,设CD经过变换后的直线l′:mx+ny=1,代入上述方程齐次化得x2+9y2+6x(mx+ny)=0,整理

图5

图6

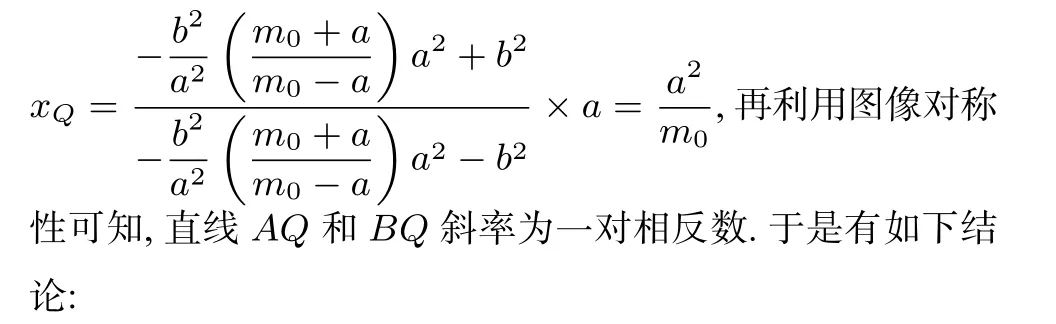
图7

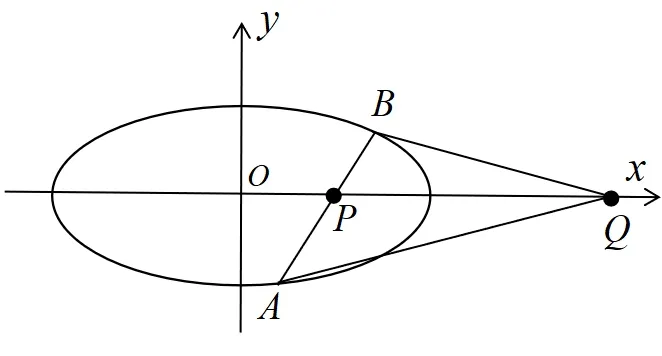
图8

图9

图10