分而视之,思广则域宽——2020年高考全国I卷理科第21题一题多解与备考策略

佛山市南海石门中学(528248) 刘依舒

教育部考试中心提出的“一核四层四翼”高考评价体系中的“四层”明确表示,“关键能力”和“学科素养”的考查,要把握两个字,“思”和“广”.思,就是对每一道试题,要多想:考查知识是什么? 解答思路有几个? 同类试题见过没? 答案组织顺畅吗? 广,就是广泛涉猎学科相关内容:除了教材、各种优质试题,还有相关读物,学科领域最新进展.函数导数一向是考生棘手的问题,如何令考生有步骤可写,有分可拿,是众多一线教师瞩目的问题.本文对2020年高考全国I 卷理科第21 题的解法进行分析,结合考试大纲与新高考的动向,参考一轮复习资料的习题,提出函数恒成立求参数取值范围问题的备考策略.

一、提出问题

二、解法分析

(一)构造函数法

(二)端点效应

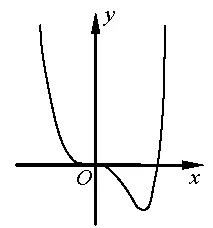
图1

端点效应有时候还需要二阶导去判断凹凸性,这一部分内容课本上并没有涉及,出题人并不希望学生使用“高观点”的做法去解题(如洛必达法则等),对学生要求高,这些都不利于提升学生的数学核心素养.而且这也不是解决该类问题的通性通法,在一轮复习中可以引用,但不值得大力提倡.于是,我们引用“分离参数法”对该题进行研究.

(三)分离参数法

(四)数形结合法

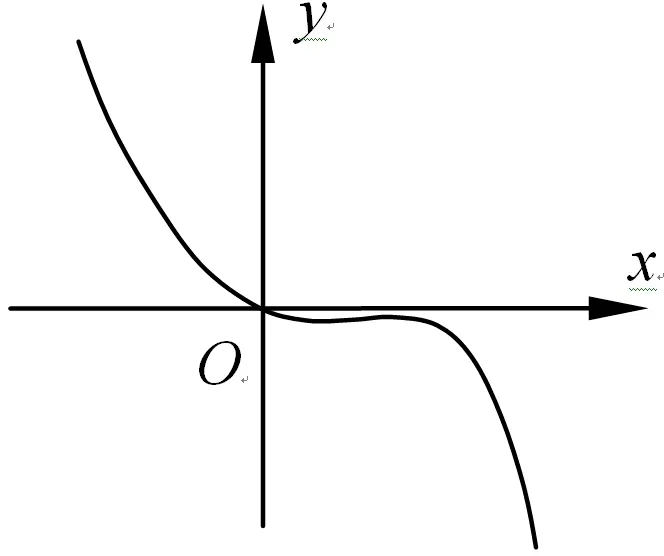
图2

该种解法中,本质上还是分离参数,由于直线性质较曲线性质易于研究,我们让参数留在一次函数中,达到“定曲动直”的效果.且这样的分离,这个函数的性质易于研究.

上述提到2017年全国Ⅱ卷函数导数题可以用端点效应解决,笔者也试了下数形结合的方法,如下:

例1(2017年高考全国Ⅱ卷)设函数f(x)=(1-x2)ex.当x ≥0 时,f(x)≤ax+1,求a 的取值范围.

解f(x)图像如图3所示.y=ax+1 为过(0,1)的直线,要当x ≥0 时使得f(x)≤ax+1恒成立,只需把相切的临界斜率a0求出来,a ≥ a0即可.f(0)=1,即y=ax+1 与f(x)在(0,1)相切即可.f′(x)=(1-2x-x2)ex,a0=f′(0)=1.所以a ≥1.

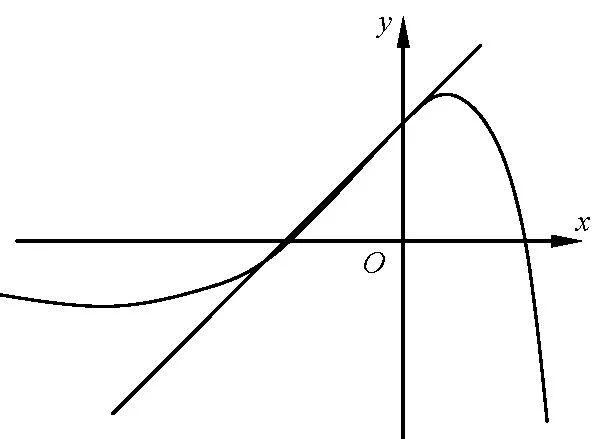
图3

后续还要有严密的代数推理否定a ＜1,但由此看来,这种解法大大节省了考生计算的时间,降低了解题的难度.也不比端点效应法来得困难.

笔者在对学生一轮复习资料进行研究后发现,对函数恒成立求参数取值范围的题目大部分都可以使用上述的数形结合的办法进行解决,下面引用两例说明:

例2(2020年石家庄市高三一检)已知函数f(x)=axex-(a+1)(2x-1).第二问:当x＞0 时,函数f(x)≥0恒成立,求实数a 的取值范围.

解 当x=1 时,f(1)=ae-(a+1)(2-1)≥0 恒成立,把一个x 值代入,先把a 的范围缩小,方便后面的式子变形.)

f(x)可变形为 xex≥为过定点的直线.要使曲线h(x)恒在直线g(x)的上方,只需把相切的临界斜率求出来,即可.解得.

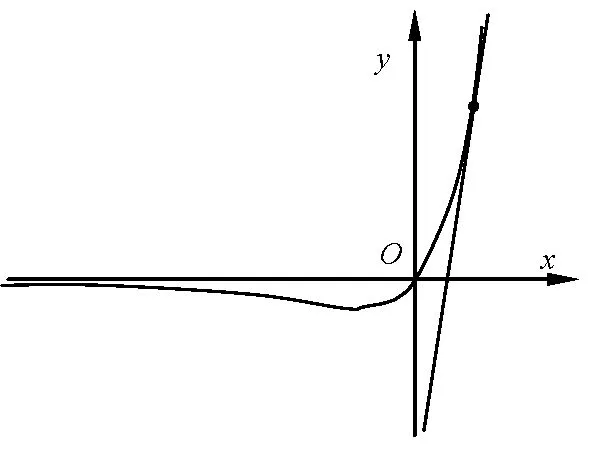
图4

例3已知函数第二问:若函数f(x)在上无零点,求a 的取值范围.

解f(x)在上无零点等价于2 ln x=0 在上无实根,也等价于h(x)与g(x)在上无交点,其中h(x)=(2-a)(x-1),g(x)=2 ln x.h(x)是过定点(1,0),斜率为k=(2-a)的直线,g(x)是确定的曲线.

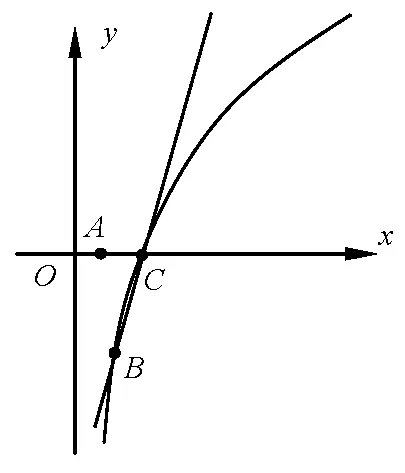
图5

三、总结提升

罗增儒教授在《数学解题关键环节的确定与教学设计》[2]中指出,数学教师必须具备将解题能力转化为他的教学能力,对此,他需要特别关注学生发生数学问题思路的某些关键环节时学生的心理环节及其过渡性中介生成,从而设计教学过程循循善诱,引导学生依靠自己的认知结构的力量,重新萌生这种思路的关键环节.所以笔者认为,在一轮复习中渗透函数导数的做题思想与方法非常重要,不能就题论题,我们应当通过教学活动帮助学生学会思考,面对函数导数题,在深入审题的基础上,必要时可回归基本初等函数及其简单组合的常见函数,将较为复杂的函数分而视之,指导学生直观思想立意要领,运用思想引领方法,让数学问题变得可视化,“横看成岭侧成峰,远近高低各不同”,站在更宽广的领域思考问题,方能达到更高的境界.