2020年高考全国Ⅲ卷理科第21题的探析

广东省佛山市乐从中学(528315) 林国红

一、题目呈现与分析

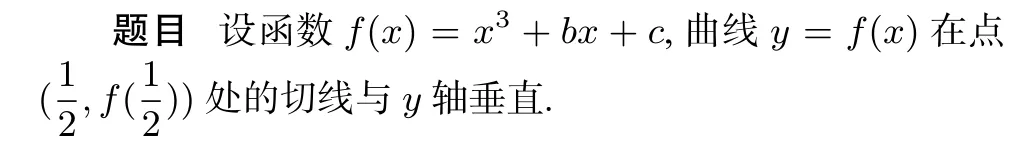
(1)求b;

(2)若f(x)有一个绝对值不大于1 的零点,证明:f(x)所有零点的绝对值都不大于1.

试题分析题目结构非常简单,是以三次函数为背景的函数导数题.知识方面主要考查导数的运算,函数的切线方程,函数零点的相关问题等;思想方面主要考查分类讨论,转化与化归,方程与函数等思想.综合考查考生对函数、方程、导数、不等式等基础知识的掌握和理解,逻辑思维转化、推理论证及运算等方面的能力.

试题分步设问,逐步推进,由浅入深,重点突出,较好地达到了考查目的.试题第(1)问的设计面向大部分考生,考生只要能理解切线的含义,准确应用导数运算法则就可以解决问题.试题第(2)问是零点有关的证明题,试题的设置为考生的解答提供广阔的想象空间,对于考生运用所学知识,寻找合理的解题策略以及推理论证能力有较高的要求.本题层次分明,区分度高,是一道能突出选拔学生功能的好题.

由于问题(1)较为简单,本文不作讨论,下面从不同视角,给出问题(2)的几种证法,抛砖引玉.

二、解法探析

1 视角一:利用零点存在性定理

评注“函数零点的存在性定理”在零点问题中应用广泛,一般来说:要求证一个函数“有且只有一个”零点,可先用“函数零点的存在性定理”证明函数存在零点;再证明函数为单调函数,即得函数零点的唯一性.其依据为:如果函数f(x)在区间[a,b]上是单调函数,并且f(a)·f(b)＜0,则函数f(x)在区间(a,b)上至多有一个零点.如果要证明函数有多个零点,一般要将区间分隔讨论解决.两个证法涉及函数的单调性、函数的零点等多个知识点,综合考查函数与方程的思想、转化与化归,分类讨论等思想,其中证法2 用到了反证法.

2 视角二:利用参数c 的范围

有零点的绝对值都不大于1.

综上,若f(x)有一个绝对值不大于1 的零点,则f(x)所有零点的绝对值都不大于1.

评注证法3 与证法4 利用已知条件“f(x)有一个绝对值不大于1 的零点”求得参数c 的范围,再通过c 的范围来证明其它零点的绝对值都不大于1.两种证法比证法1 与证法2 减少了分类讨论的步骤,解答过程更简捷,其中证法4 利用“三角换元”及三倍角公式,方法更巧妙.两个证法的难点在于三次不等组的求解.

3 视角三:利用二次函数或二次方程

综上,若f(x)有一个绝对值不大于1 的零点,则f(x)所有零点的绝对值都不大于1.

不等式(2t±1)2≥0 显然成立,从而f(x)所有零点的绝对值都不大于1.

综上,若f(x)有一个绝对值不大于1 的零点,则f(x)所有零点的绝对值都不大于1.

评注两个证法都要将三次多项式进行因式分解,这也是证法的难点.其中证法5 因式分解后利用二次函数的相关性质进行证明,证法6 因式分解后利用二次方程及不等式进行证明,两个证法都不涉及到导数的有关知识.

4 视角四:利用不等式

综上,若f(x)有一个绝对值不大于1 的零点,则f(x)所有零点的绝对值都不大于1.

评注证法7 利用均值不等式证明结论,证法8 利用柯西不等式证明结论,两个证法都不涉及到导数的有关知识,证明思路新颖巧妙.

三、解后小结

以上的几种证法,从不同的角度出发思考问题,各显神通.这充分体现数学高考题的不拘一格,一道试题往往考查多种能力、多种思想方法;同时,高考试题在命制时充分考虑到考生数学能力的个体差异,多数试题的解答方法、思维方式不是唯一,一题多解,给考生提供了较大的发挥空间.这样通过方法的选择、解题时间的长短,甄别出考生能力的差异,达到精确区分考生的目的.

从不同的思维角度分析同一道题目,得到不同的解题方法,一题多解的方式增加了题目涉及的知识广度,以一带多,减少了考查同样多的知识所需的题量.从数学知识的角度来看,通过解题发现知识的相互联系,体会知识之间的转化过程,从多角度地思考和发现问题,构建知识网络体系.这样,在学习基础知识、掌握基本技能的同时,能培养学生思维的广阔性、深刻性、灵活性以及创新性,能够使学生对学习的内容有一个整体的认识,并将知识融会贯通,举一反三,开阔眼界,活跃思维,从而提炼出数学思想与方法,这正是数学教学的核心.

四、试题的背景探析

1 余弦的多倍角公式

我们知道cos(nθ)可以表示成关于cosθ 的多项式:cos(0)=1,cos(x)=cos x,cos(2x)=2cos2x - 1,cos(3x)=4cos3x-3 cos x,cos(4x)=8cos4x-8cos2x+1,cos(5x)=16cos5x-20cos3x+5 cos x,···.

2 切比雪夫多项式

记Tn(x)=cos(n·arccos x),则Tn(x)是一个n 次多项式,称为n 次切比雪夫多项式,其中x ∈[-1,1],n ∈N.于是T0(x)=1,T1(x)=x,T2(x)=2x2-1,T3(x)=4x3-3x,T4(x)=8x4-8x2+1,T5(x)=16x5-20x3+5x,···.切比雪夫多项式有许多良好的性质,例如:

性质1Tn(cos θ)=cos(nθ),θ ∈R,n ∈N.

性质2当|x|≤1 时,|Tn(x)|≤1,x ∈R.

性质3函数列{Tn(x)}满足二阶递推关系Tn+2(x)=2xTn+1(x)-Tn(x).

由证法4,可以发现试题与余弦的三倍角公式有关.事实上,这正是试题的命题背景:切比雪夫多项式的性质1 与性质2 的综合应用,即当n=3 时,若|x| ≤1,当且仅当|4x3-3x|≤1.

切比雪夫多项式是高等数学的内容,它的相关结论有着广泛的应用,将其“镶嵌”在高考题中可谓独具匠心,命题者借助具有高等数学背景的试题来考查学生对知识的掌握程度和继续学习的潜力,虽然试题的立意是“高等”的,但解法是“初等”的,不会在解答时对考生造成思维障碍,考生只要具备灵活运用高中数学知识的相关的能力就能完成解答.这正好契合了新课程标准的要求:获得必要的数学基础知识和基本技能,理解基本的数学概念、数学结论的本质,了解概念、结论等产生的背景与应用,体会其中所蕴含的数学思想和方法以及它们在后续学习中的作用.

近年来,高考的命题者通过挖掘高等数学中的一些素材来命制高考试题,此类试题也逐渐引起老师们的关注.但这并不意味着要将过多的高等数学知识下放到中学里来,加重中学的负担,应该是教师能站在高观点的角度看待问题,找到问题的本质内涵,更好地指导中学的数学教学.