先论证再构造 先构造再论证

李含进 钱朝晖

(江苏省锡山高级中学，214174)

逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养. 主要包括两类:一类是从特殊到一般的推理,推理形式主要有归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎. 在教学中,要有意识地重视从特殊到一般的推理能力的培养,这是逻辑推理的重要组成部分之一,也是培养学生“数学地”观察事物,对问题“数学地”思考,从而用数学独特的逻辑思维模式解决问题,这是学生学习数学最重要的价值所在.

本文结合2019年江苏、浙江高考最后一题谈一谈从特殊到一般的推理.尤其是先论证再构造与先构造再论证推理能力等在解决问题中的应用.

一、先论证再构造

例1(2019年江苏高考题)定义首项为1且公比为正数的等比数列为“M-数列”.

(1)已知等比数列{an}满足:a2a4=a5,a3-4a2+4a1=0,求证:数列{an}为“M-数列”;

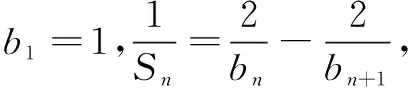
(i) 求数列{bn}的通项公式;

(ii) 设m为正整数,若存在“M-数列”{cn}(n∈N*),对任意正整数k,当k≤m时,都有ck≤bk≤ck+1成立,求m的最大值.

分析与解第(1)问,由题意分别求得数列的首项和公比，即可证得题中的结论;第(2)问,(i) 由题意利用递推关系式讨论可得数列{bn}是等差数列,据此即可确定其通项公式,这里不再赘述.本题最体现逻辑思维考查的是第(ii)问.

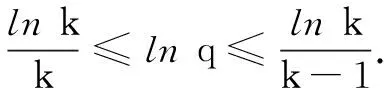
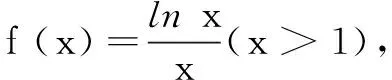
令f′(x)=0,得x=e，列表，f(x)在(1,e)上单调递增,在(e,+∞)上单调递增.

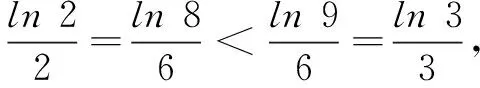
因此，所求m的最大值不小于5.

若m≥6,分别取m=3,6,得3≤q3,且q5≤6,从而q15≥243,且q15≤216.

所以q不存在故所求m的最大值小于6.

综上,所求m的最大值为5.

在上述解答中,构造函数略显突兀，不太符合学生的思维习惯.若采用先通过估算,求出公比q的取值范围,再构造出满足题意的数列即可.思考过程如下:由(i)知,bk=k,k∈N*.因为数列{cn}为“M—数列”,设公比为q,所以c1=1,q>0.因为数列{cn}为“M-数列”，设公比为q,所以c1=1,q>0.因为ck≤bk≤ck+1,所以qk-1≤k≤qk,其中k=1,2,3,…,m.

特殊地当k=1时,有q≥1,于是当q=1时,只有k=1满足题意,此时m的最大值为1,可猜想q>1时,可能还有更大的m满足题意.

而当q>1时,随着k的逐渐增大,qk以指数函数增长,增长的幅度更快,故而预判满足qk-1≤k≤qk的k不会很大,否则应该能从中找到矛盾. 分别取k=1,2,3,…得到1≤q1≤2≤q2≤3≤q3≤4≤q4≤5≤q5≤6≤q6≤7≤…

(*)

观察(*)式,容易发现,2≤q2与q6≤7是矛盾的,那就说明k≤6,再思考k=5是否成立呢?不难发现3≤q3与q5≤6也是矛盾的,故而k≤5.

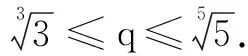
本题先论证再构造的数学解题思维模式,很好地体现了对学生思维方式、思维模式和思维深度的考查,是一道不可多得的具有较强选拔功能的试题.

二、先构造再论证

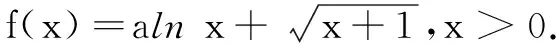
注e=2.718 28…为自然对数的底数.

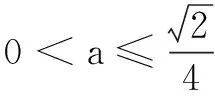
从本题的思维展开过程中,我们不难看到,解决问题的突破口在于通过特殊值求解满足题设的必要条件,进而证明必要条件即为充分条件,这是本题的题眼.这同样需要学生具备非常深厚的逻辑思维能力,转化化归以及构造函数的变形能力.本题和江苏高考最后一题有异曲同工之妙.

三、感悟与思考

(1)新授课、习题课和复习课本质相同,都是为了培养学生的数学核心素养.在平时的课堂教学中,我们要有意识地渗透预判、估算、结构变形、特殊化，逐步培养和必要性、充分性、逻辑论证等相关的数学逻辑思维.逻辑思维能力的培养不是一蹴而就的,需要教师的示范、引领和参与,逐步突破思维的难点.

(2)对数学教学中的最能体现数学逻辑思维的部分章节,如函数、数列、不等式以及数学归纳法等,要善于挖掘培养学生逻辑思维能力的素材,根据一些经典的逻辑思维方式展开数学问题.通过必要的拓展,让数学知识在高考范围的外延处进行有效地延伸.

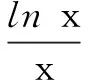
在数学归纳法的教学中,教材的要求是只讲授到第一数学归纳法,但是从知识体系的完备性角度和学生认知结构的完整性角度看,我们教学中需要渗透第二数学归纳法以及数学归纳法证明加强命题.如江苏2010年高考理科加试第23题:“已知∆ABC的三边长都是有理数,求证:对任意正整数n,cosnA是有理数”.本题可以用数学归纳法证明加强命题“对任意正整数n,cosnA和sinA·sinnA都是有理数”.也可用第二数学归纳法证明,即假设n≤k(k∈N*)时,cosnA是有理数,则coskA,cos(k-1)A都是有理数,也可以很方便地证明结论.

在数学教学中,教师要善于挖掘知识的外延,善于引领学生养成较强的逻辑思维能力,并建立强大的逻辑思维体系.这样，当学生遇到较复杂的体现逻辑思维考查的问题时,可以多一些思考的方向,多一些解决问题的手段和方法.

(3)数学六大核心素养,旨在培养学生用数学思维思考问题、解决问题的能力.数学教育教学的核心价值,旨在培养学生用数学的方式和方法解决问题的习惯和素养,这也是数学教师最应关注的数学教育价值.