揭开迷雾 追根溯源——例说圆锥曲线中条件 “直线与椭圆的交点”的多元表征

张 震

(江苏省常州市戚墅堰实验中学，213011)

圆锥曲线是高中数学非常重要的一个内容,既是高考的热点也是难点.学生在处理圆锥曲线章节内容时常常感觉头绪很多,似乎有很多种解法,却不知该如何选择.归根结底，这是圆锥曲线中某些条件表征的多元化给学生带来的困惑.要想解决这一问题就需要学生透过一题多解的现象,追溯条件多元化表征的本质.

本文将通过“直线与椭圆的交点”这一圆锥曲线中最为常见的条件的多元表征来阐述上述观点.

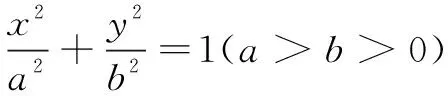
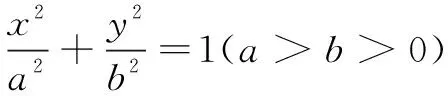
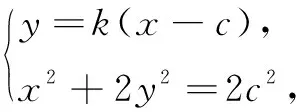
(1+2k2)x2-4ck2x+2c2(k2-1)=0.

其中Δ=16c2k4-4·2c2(k2-1)(1+2k2)=16c2k4-8c2(2k4-k2-1)=8c2(1+k2)>0.

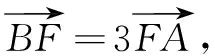
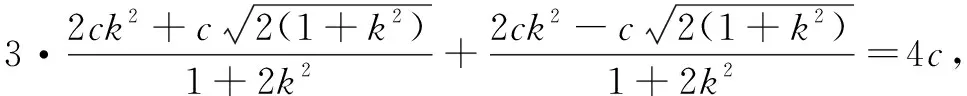
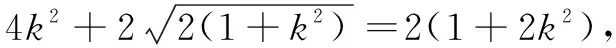
又因为k>0,所以k=1.

表征分析解法1是利用斜率k设出直线方程,然后将椭圆方程与直线方程联立,通过求解方程组得出A，B两点的横坐标,从而直接表征“A，B两点为直线与椭圆的交点”这一条件.此方法虽然直接易得,但是庞大的计算量却常常令学生望而却步.

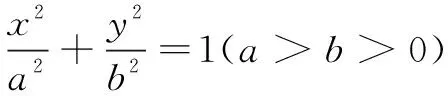
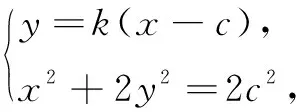
(1+2k2)x2-4ck2x+2c2(k2-1)=0.

其中Δ=16c2k4-4·2c2(k2-1)(1+2k2)=16c2k4-8c2(2k4-k2-1)=8c2(1+k2)>0.

设A(x1,y1),B(x2,y2),则

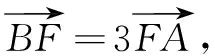
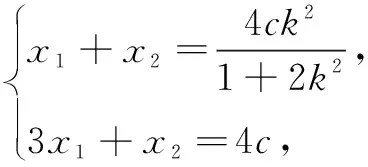
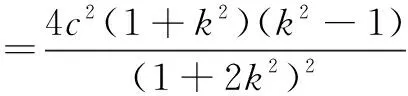
解得k2-1=0.

又因为k>0,所以k=1.

表征分析解法2与解法1的解题依据是一样的,都是根据曲线交点的坐标与方程组的解之间的对应关系,但与解法1不同的是在表征“A，B两点为直线与椭圆的交点”这一条件时,抓住了A，B两点坐标之间的整体关系,即通过联立所得方程的韦达定理来刻画.这样的表征方法,优化了解法1中求解坐标时运用求根公式带来的复杂运算.

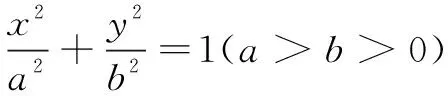
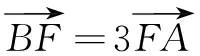
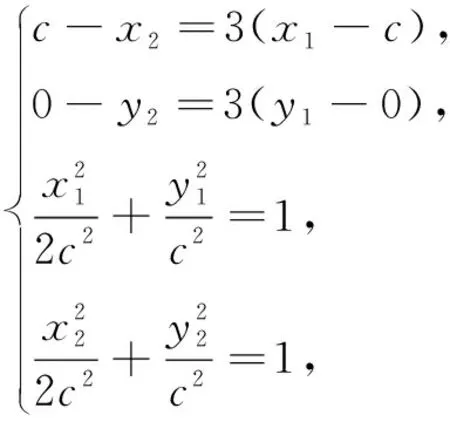
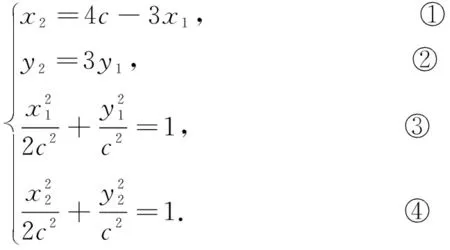
① ② 代入③ ④ 得

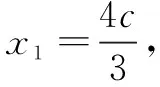
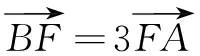
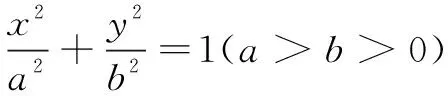
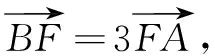
因为A,B在椭圆上,且点F是椭圆右焦点,所以，由向量坐标运算及椭圆的焦半径公式，可得

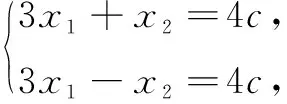
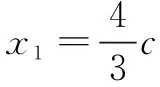
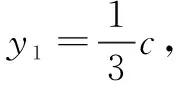
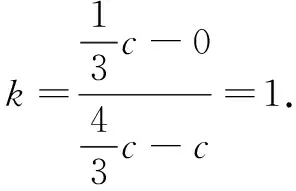
表征分析解法4是一个非常漂亮的解答方法,它一方面是延续了解法3的思路,即通过坐标来表征“A，B两点为直线与椭圆的交点”这一条件;另一方面是对解法3的优化,即立足点F是椭圆右焦点这一特殊情况,通过椭圆的第二定义得出的焦半径公式来表征“点在椭圆上”这一条件.从解答过程可以看出,这样巧妙的表征方法使得问题求解过程得到简化:未知量从4个减少为2个,方程组的次数从2次降低为1次,从而运算变得非常简单,问题的求解速度得到了大大地提高.

解法5如图1,取左焦点F1,连结AF1,BF1.

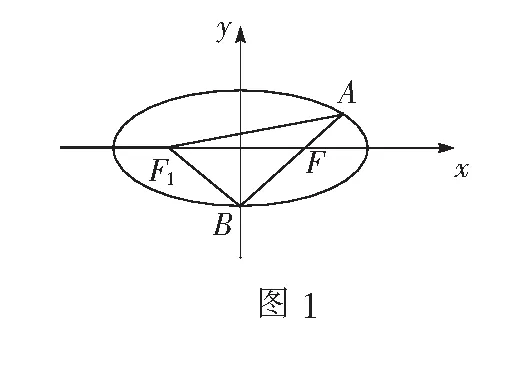
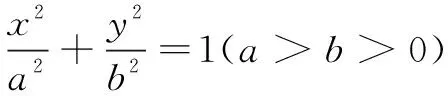
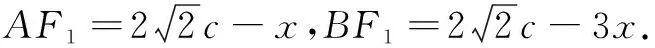
在∆AF1F中,

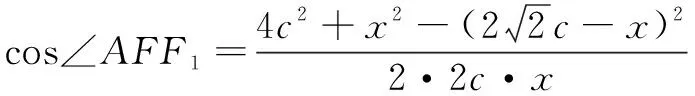
在∆BF1F中,

因为cos∠AFF1+cos∠BFF1=0,

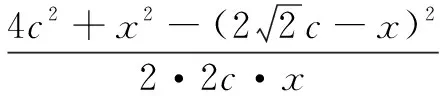
化简得

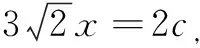
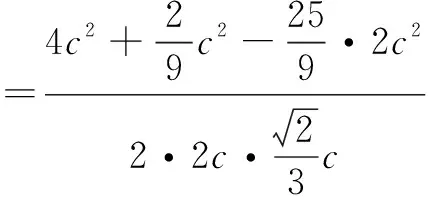
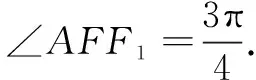
表征分析解法5的思路与前面几种解法完全不同,此解法中用第一定义即椭圆上的点满足到两焦点的距离之和等于长轴长来表征“A，B两点在椭圆上”,用相邻补角的余弦值互补即cos∠AFF1+cos∠BFF1=0来表征“A，B两点在过点F的直线上”,通过两次余弦定理来建立边长之间的关系,最终得出所求倾斜角的大小,进而得出所求斜率.

解法6如图2所示,分别过A，B作右准线的垂线,垂足为A′，B′,过A作BB′的垂线,垂足为M.

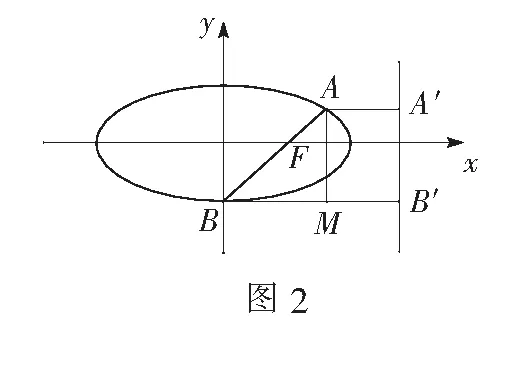
设AF=x,BF=3x,

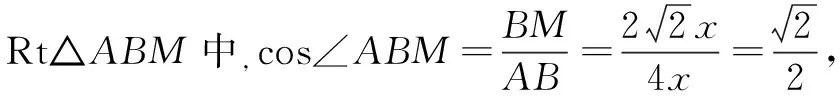
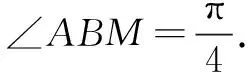
表征分析解法6从解答过程来看应该是六种解法中最为简单的方法,究其原因可以发现，表征“A，B两点在椭圆上”是运用的椭圆第二定义,在表征“A，B两点在过点F的直线上”运用的是线段长度关系即AB=AF+FB=4x,然后通过解直角三角形得出结果.这一解法十分简洁精彩,将椭圆第二定义的比值完美地融合在直角梯形和直角三角形等一些特殊的图形中,将几何法的优势得以凸显.