中学数学中的适应性问题举偶

何建东 俞菊妃

(浙江省绍兴市越州中学，312075) (浙江省绍兴文理学院附中，312000)

纵览近年来的中高考以及数学竞赛试题,我们常能看到这样一类问题,要求学生即时接受题目给出的新事物,根据平时所学的数学知识,去适应新情况,进行探索,求得结果.我们把这一类问题称之为“适应性问题”.

“适应性问题”具有情境新、立意新、形式新等特点,一般需要学生具备较强的自主学习能力.通过阅读题意,即时理解新的概念、公式、规则等,然后按照“从新情境中获取信息——分析处理信息——转化为数学问题——获得原问题的解答”的步骤进行“边适应边解答”式的问题解决[1].

在数学教学中,教师若能将此类问题进行归类整理,为学生作专门系统性的讲析,可以让学生增强适应能力,提高对此类问题的解决效率．本文根据笔者廿多年的教学实践经验,归纳整理出以下七类“适应性问题”,试分别举例评析.

一、适应一种“新运算”

例1对正实数x,y,定义运算“*”:x*y=axy+b+7,已知1*2=989, 2*3=1 003,则2*9的值为( )

(A)2 009 (B)2 010

(C)2 011 (D)2 012

解析对于这类临时定义的“新运算”,解题的关键是将具体的x,y正确地代入等号右侧的代数式,将“新运算”的要求转化为熟悉的知识,从而给予解决.

根据题意,可列出关于a,b的方程组

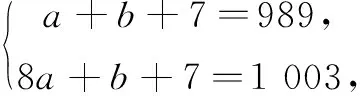
解得a=2,b=980.

故x*y=2xy+987,2*9=210+987=1 024+987=2 011,选C.

例2在正实数集上定义一种运算“☆”:当a≥b时,a☆b=b3;当a

解析根据题意,需要分3≥x和3

若3≥x,则3☆x=x3=27,得x=3;

二、适应一个“新符号”

例3定义符号[x]表示不超过x的最大整数.如，[2.1]=2,[3]=3,[-1.5]=-2.现已知[x]=3,[y]=0,[z]=1,试求[x+y-z]所表示的数的范围.

∴1

例4现定义符号如下:f(x)表示以x为自变量的函数,其中x为任意正数,对任意正数x,y恒有f(x·y)=f(x)+f(y)成立.已知f(8)=3,试求f(32)的值.

解析本题所给的符号f(x)其实就是高中数学中的函数符号,若未给出具体的函数解析式,f(x)是一个抽象函数.解决这类问题需要学生有较强的理解能力,其关键是将条件“对任意正数x,y恒有f(x·y)=f(x)+f(y)成立”看成为一个公式,灵活恰当地给变量x,y进行赋值,或者结合中学所学的符合此条件具体某个基本初等函数辅助思考.

可先将f(8)按条件形式进行变形:f(8)=f(2×4)=f(2)+f(4),

类似地，有f(4)=f(2×2)=f(2)+f(2)=2f(2).

∴3f(2)=3,得f(2)=1.

再将所求f(32)变形:f(32)=f(4×8)=f(4)+f(8)=2+3=5.

说明本题所给的函数f(x)可以用高中数学中的对数函数f(x)=logax(a>0,且a≠1)作为具体一个函数来辅助分析.由条件f(8)=3易知其中的a=2.常见类似的等式还有f(x+y)=f(x)·f(y)(指数函数)，f(x+y)=f(x)+f(y)(正比例函数)，f(x·y)=f(x)·f(y)(幂函数)等,此题中的等式还可以推广为f(x·y·z)=f(x)+f(y)+f(z)，f(xn)=nf(x)等.

三、适应一种“新图形”

例5将已知线段AB等分为A0A1,A1A2,A2A3,…,An-2An-1,An-1An,其中A0=A,An=B,点A涂红色,点B涂蓝色,其它n-1个点任意涂红色或蓝色之一.如果一个等分线段的两端点有不同颜色,那么称这条线段为“好线段”.试证:这n条线段中共有奇数条“好线段”.

解析本题新给出一种“新图形”——“好线段”.理解其意思:“一个等分线段的两端点有不同颜色”是解题的关键.

不妨设最后一条“好线段”是AkAk+1.若k=0,则仅有一条“好线段”,得证.若k≠0,则Ak与A0同为红色(否则Ak+1为红色,由于B为蓝色,则不论Ak+1与B之间有否蓝色点,将有新的“好线段”出现,与假设矛盾),注意到Ak与A0之间若有“好线段”,必是红蓝“好线段”与蓝红“好线段”成对出现,所以Ak与A0之间有偶数条“好线段”,加上最后一条,共有奇数条“好线段”.

四、适应一个“新集合”

例6非空集合G关于运算⨁满足:(1)对任意的a,b∈G,都有a⨁b∈G；(2)存在e∈G,都有a⨁e=e⨁a=a,则称G关于运算⨁为“融洽集” .现给出下列集合和运算:

①G={非负整数},⨁为整数的加法；

②G={偶数},⨁为整数的乘法；

③G={平面向量},⨁为向量的加法；

④G={二次三项式},⨁为多项式加法；

⑤G={虚数},⨁为复数的乘法.

其中G关于运算⨁为“融洽集”的是______(写出所有“融洽集”的序号)

解析本题是以近世代数中群的定义为背景命制的,同时涉及中学数学中的整数、向量、多项式、复数等知识素材.经过命题者的精心设计和包装,以“融洽集”的形式出现,展示了一个全新的问题.解决这个问题的关键是阅读理解“融洽集”的定义,综合运用多种数学思想方法,分别检查所给答案是否同时满足其定义的两个条件(满足需证明,不满足需举反例).以下进行逐一分析.

①G={非负整数},⨁为整数的加法,满足任意a,b∈G,都有a⨁b∈G；且令e=0,有a⨁0=0⨁a=a,所以① 符合要求;

②G={偶数},⨁为整数的乘法,若存在a⨁e=a×e=a,则e=1,矛盾, ∴② 不符合要求;

③G={平面向量},⨁为平面向量的加法,取e=0,满足要求, ∴③ 符合要求;

④G={二次三项式},⨁为多项式的加法，两个二次三项式相加得到的可能不是二次三项式，所以④不符合要求;

⑤G={虚数},⨁为复数的乘法，两个虚数相乘得到的可能是实数, ∴⑤ 不符合要求.这样G关于运算⨁为“融洽集”的有① ③.

五、适应一种“新规则”

例7有红、黄、蓝三种颜色的玻璃片,它们的张数分别是13，15，17.规定进行以下的操作:把两块颜色不同的玻璃片上的颜色擦去,涂上第三种颜色,问是否可以通过有限次操作,使得每一块玻璃片都涂上了同一种颜色?请证明你的结论.

解析针对此类问题,适应“新规则”的要求是解决问题的关键.

不妨假设某一次调整之前,三种颜色的玻璃片数分别是x，y，z,经过一次调整之后,只可能变成以下三种情况之一:

红黄蓝 x-1y-1z+2 x-1y+2z-1 x+2y-1z-1

讨论红、黄两种颜色玻璃片数之差,对比三种情况,分别是:

(x-1)-(y-1)=x-y；

(x-1)-(y+2)=x-y-3；

(x+2)-(y-1)=x-y+3.

说明任何两色的玻璃片数之差在操作前后,被3除的余数相同,而初始状态上,红、黄两色玻璃片数之差为2,不能被3整除,故最终每块玻璃片不可能涂上同一种颜色(如蓝色),否则将有另两种颜色的玻璃片数之差为0,将能被3整除.

六、适应一类“新数”

例8将正整数N接写在每一个正整数的右面,如果得到的新数都能被N整除,那么称N为“魔术数”,在小于130的正整数中,“魔术数”的个数是多少?

解析本题的知识范畴为整数和整除,利用整除性质进行考虑是解决问题的关键.

设a为“魔术数”,把它接写在任一正整数的右面,得到一个新数,按a的位数分类讨论:

(1)若a是一位数,则可将新数表示为10x+a,能被a整除,即对任一正整数x,10x都能被a整除,即10应是a的倍数,这样的a只能是1,2,5共3个;

(2)若a是两位数,则可将新数表示为100x+a,能被a整除,即对任一正整数x,100x都能被a整除,即100应是a的倍数,这样的a只能是10,20,25,50共4个;

(3)若a是三位数,则可将新数表示为1 000x+a,能被a整除,即对任一正整数x,1 000x都能被a整除,即1 000应是a的倍数,又a<130,这样的a只能是100,125共2个.

所以,符合条件的“魔术数”共有3+4+2=9个.

七、适应一种“新数组”

例9如果一个正整数的每个素数因数都至少是二重的(即每个素数因数乘方次数都大于或等于2),那么称这个正整数为“漂亮数”.如果两个相邻的正整数都是“漂亮数”,那么称这两个数构成的数组为“孪生漂亮数组”.例如相邻的正整数8,9就构成一个“孪生漂亮数组”,请你再找出两个“孪生漂亮数组”来.

解析根据题意,“孪生漂亮数组”是由两个相邻的“漂亮数”构成,而两个“漂亮数”的乘积仍然是“漂亮数”,因此,可以考虑借助已知的一个“孪生漂亮数组”寻找解题突破口.

设(n,n+1)是一个“孪生漂亮数组”,可知4n(n+1)仍然是“漂亮数”.

而4n(n+1)+1=4n2+4n+1=(2n+1)2是一个完全平方数,必也是“漂亮数”.

所以 (4n(n+1),4n(n+1)+1)也是一个“孪生漂亮数组”.

已知(8,9)是一个“孪生漂亮数组”,

当n=8时,4n(n+1)=288,4n(n+1)+1=289,故(288,289)为一个“孪生漂亮数组”.

又当n=288时,4n(n+1)=332 928,4n(n+1)+1=332 929,故(332 928,332 929)也为一个“孪生漂亮数组”.

随着数学教学实践的发展,“适应性问题”将越来越多地进入教师和学生的视野.如果我们能做一个有心人,将这一类问题进行及时的收集和整理,必将为数学教学和研究注入新的活力.