无心插柳柳成荫——一节“失控”的复习课

焦永垚 李强龙

(甘肃省兰州市第六中学，730060)

课堂是一个动态的生成过程,布卢姆认为:“人们无法预料教学所产生的成果的全部范围.没有预料不到的成果,教学也就不成为一种艺术了.”在一节平面向量基本定理的复习课上,笔者与以往一样,先引导学生回忆本节课的知识点、题型及解题方法,然后给出例题.结果却出现了意料之外的教学过程,收到了意想不到的教学效果.兹介绍如下.

一、问题呈现

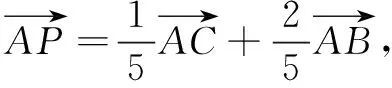
二、解法展示

师:平面向量中三角形面积之比问题是高考数学中的热点问题之一,解法灵活多变,请同学们先思考这道题如何解?(本来笔者打算引导学生用平面向量基本定理的知识去解决,但是经短暂思考后，学生1举手示意并走上讲台.)

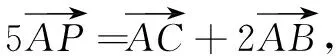
师:非常棒!平面向量的运算掌握得不错,基本功很扎实,这个思路的关键是把三角形面积之比转化为相应三角形的线段之比,还有不同的思路吗?

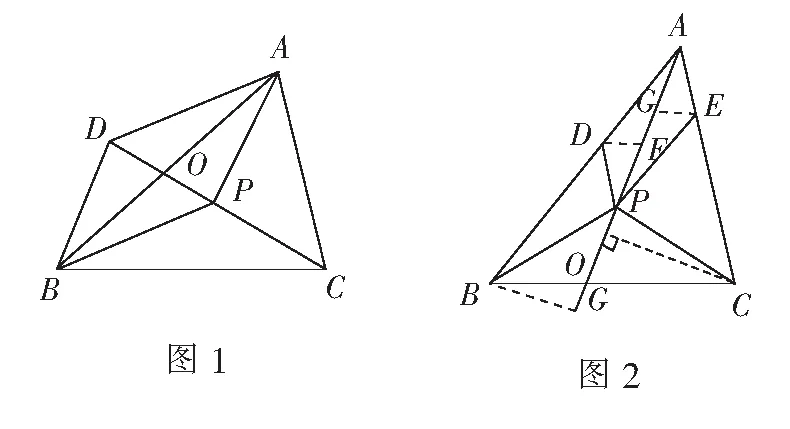
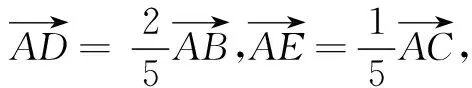
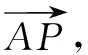
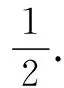
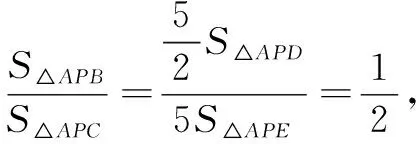
此时课堂已经完全“失控”,同学们热烈讨论,各抒己见.

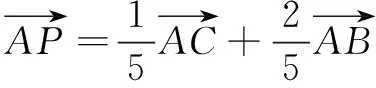
师:非常精彩!当然我们也可建立斜坐标系解决,过程是一样的.既然可以特殊成直角三角形,那也还可以特殊成别的三角形.

学生6:对,可以将∆ABC特殊为等腰直角三角形,如图5.此时平行四边形ADPE为矩形,所以

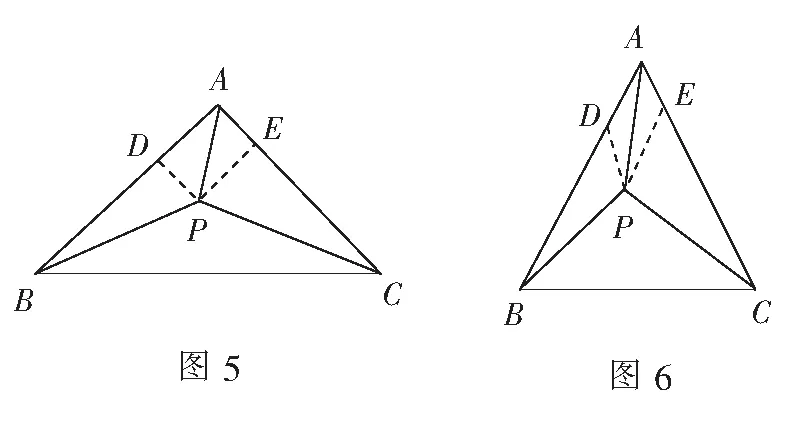
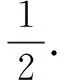
学生7:其实，将∆ABC特殊为等腰三角形就够了,如图6，同样作出平行四边形ADPE.设AB=AC,则

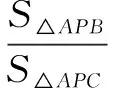
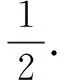
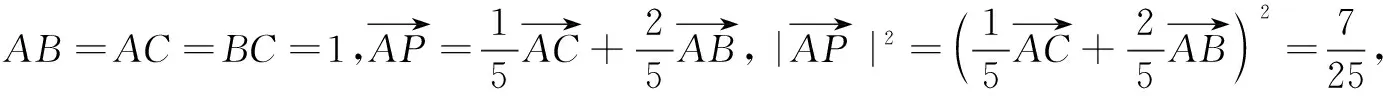
此时下课铃已响,同学们仍意犹未尽.

师:看来这个有意义的问题只能留到课后同学们自己去完成了.

三、得出结论

经过同学们课后的努力,教师指导总结,得到了下面的结论.

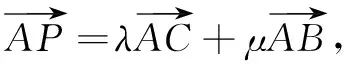
结论2已知∆ABC的内角A,B,C的对边分别为a,b,c,若点I为∆ABC的内心,则∆AIB，∆AIC和∆BIC的面积之比为c∶b∶a.

结论3已知点O为∆ABC的外心,则∆AOB，∆AOC和∆BOC的面积之比为sin 2C∶sin 2B∶sin 2A.

结论4已知点G为∆ABC的重心,则∆AGB，∆AGC和∆BGC的面积相等.

结论5已知点H为∆ABC的垂心,则∆AHB，∆AHC和∆BHC的面积之比为|tanC|∶|tanB|∶|tanA|.

从教学过程不难看出，本节课其实完全偏离了笔者的本意.本来打算从知识点到题型,再到解题方法,按部就班完成设计好的教学内容,但是学生1的思路就没有按照笔者预先设计的思路走,真是一石激起千层浪,后面学生的思路层出不穷.笔者不忍心扼杀同学们学习热情,所以就顺其自然,结果收到了意想不到的效果.同时在课后经过同学们的团结合作,得出有意义的结论,极大激发了学生探究问题的兴趣和团结合作的精神,培养了学生的学习积极性,发散了学生的思维,提升了学生的求知欲.

我们不应拘泥于教学活动的外在形式,而忽略了教会学生思考这一数学教学的本质.罗增儒说过,“讲课是一门遗憾的艺术”,任何事情都是辩证的,真可谓失之东隅,收之桑榆.本节课本身是一节高三复习课,我们不应该把这样的课堂教学变成教师的“一言堂”.教师应该适时给予学生展示自己思维的机会,从这一点上讲,本节课是一节成功的课,高效的课.