递推数列问题的命题特色及解法赏析

鲁 彬

(江苏省姜堰第二中学，225500)

已知数列的第1项(或前几项),且从第2项(或某一项)开始的任一项an与它的前一项an-1(或前几项)间的关系可以用一个公式表示,这个公式称为数列的递推公式, 这样的数列称为递推数列.等差数列和等比数列都是特殊的递推数列,是高考中常规题型，而一般的递推数列是数学竞赛中的热点．近年来,高考的压轴题出现了新风向:把递推数列与其他知识交汇命题,通过常规方法解决递推数列的通项公式.这样命题既不超纲,又颇有特色.兹分类举例说明如下.

一、知识交汇，焕发递推数列新活力

1.递推数列与排列组合的交汇

例1(2018年江苏卷第23题)设n∈N*,对1,2,…,n的一个排列i1,i2,…,in,如果当sit,则称(is,it)是排列i1,i2,…,in的一个逆序,排列i1,i2,…,in的所有逆序的总个数称为其逆序数.例如，对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记fn(k)为1,2,…,n的所有排列中逆序数为k的全部排列的个数.

(1)略;

(2)求fn(2)(n≥5)的表达式(用n表示).

解(1)略.

(2)对于一般n(n≥4)的情况,逆序数为0的排列只有一个即1,2,…,n,所以fn(0)=1.

逆序数为1的排列只需将排列1,2,…,n中的任意相邻两个数字调换位置即可,所以fn(1)=n-1.

为计算fn+1(2),当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排列,而n+1在新排列中的位置只可能是最后三个位置.

因此,fn+1(2)=fn(2)+fn(1)+fn(0)=fn(2)+n.

当n≥5时,

fn(2)=[fn(2)-fn-1(2)]+[fn-1(2)-fn-2(2)]+…+[f5(2)-f4(2)]+f4(2)

=(n-1)+(n-2)+…+4+f4(2)

点评本题通过新型定义“逆序数”与递推数列交汇,既考查计数原理、排列等基础知识,又考查运算求解能力和推理论证能力,通过本题可以培养学生的数学抽象、逻辑推理等核心素养.

2.递推数列与概率的交汇

例2(2019年全国Ⅰ卷理科第21题)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.

(1)略;

(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.

(i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;

(ii)求p4,并根据p4的值解释这种试验方案的合理性.

解(2)(i)∵α=0.5,β=0.8,

∴由(1)得,a=0.4,b=0.5,c=0.1.

因此pi=0.4pi-1+0.5pi+0.1pi+1(i=1,2,…,7),

故0.1(pi+1-pi)=0.4(pi-pi-1),即(pi+1-pi)=4(pi-pi-1).

又p1-p0=p1≠0,故{pi+1-pi}(i=0,1,2,…,7)为公比为4,首项为p1的等比数列.

(ii) 由(i)，可得

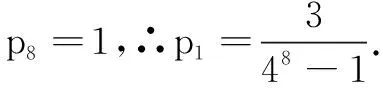
p4表示最终认为甲药更有效的概率.

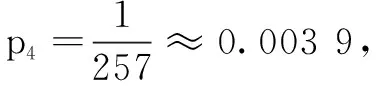
点评本题将概率与递推数列交汇,考生通过数学阅读，从题目中提取有效信息,建立数学建模,运算求解后判断试验方案的合理性.通过本题可以培养学生的数学建模,数学运算，数据分析等核心素养.

递推数列除了与排列组合、概率知识交汇以外,还可以与立体几何、解析几何、分形等知识交汇,这种热点问题的命题方式和求解过程能够促进学生获得“四基”,提高“四能”,也能使学生发展数学核心素养.

二、教材内容赋予递推数列新生命

三、常规解法打开递推数列新思路

在数学竞赛中,特征根法、不动点法是解决递推数列的常用方法,但毕竟参加数学竞赛的同学具有较强的数学能力,这些方法对一般学生提出了很高的要求和挑战.因此，下面介绍学生比较熟悉的“待定系数法”来解决一类递推数列的通项公式问题.

题型1形如an+1=pan+q(p≠1,pq≠0)的递推数列.

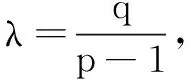
例3数列{an}满足:a1=1,an+1=2an+1,求数列{an}的通项公式.

解易知an+1+1=2(an+1)且a1+1=2≠0,{an+1}是以2为首项,2为公比的等比数列,故an+1=2n,an=2n-1.

题型2形如an+1=pan+an+b(p≠0,p≠1,a≠0)的递推数列.

求解策略令an+1+x(n+1)+y=p(an+xn+y),与原式比较系数解出x,y,从而转化为等比数列{an+xn+y}.

例4数列{an}满足:a1=4,an+1=3an+2n+1,求数列{an}的通项公式.

解设an+1+x(n+1)+y=3(an+xn+y),an+1=3an+2xn+2y-x,∴x=1,y=1,故an+1+(n+1)+1=3(an+n+1),a1+1+1=6≠0,∴{an+n+1}是以6为首项,3为公比的等比数列,故an+n+1=6×3n-1,∴an=2×3n-(n+1).

题型3形如an+1=pan+an2+bn+c(p≠0,p≠1,a≠0)的递推数列.

求解策略令an+1+x(n+1)2+y(n+1)+z=p(an+xn2+yn+z),与原式比较系数解出x,y,z,从而转化为等比数列{an+xn2+yn+z}.

例5数列{an}满足:a1=4,an+1=3an+2n2+4n+2,求数列{an}的通项公式.

解令an+1+x(n+1)2+y(n+1)+z=3(an+xn2+yn+z),得an+1=3an+2xn2+2(y-x)n-x-y+2z,对照原式可知x=1,y=z=3.

∴an+1+(n+1)2+3(n+1)+3=3(an+n2+3n+3),a1+12+3×1+3=11≠0,

∴{an+n2+3n+3}是以11为首项,3为公比的等比数列.

故an+n2+3n+3=11×3n-1,

∴an=11×3n-1-(n2+3n+3).

题型4形如an+1=pan+qn+1(pq(p-1)(q-1)≠0)的递推数列.

例6数列{an}满足:a1=1,an+1=3n+1+3an,求数列{an}的通项公式.

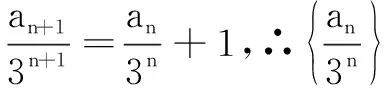
题型5形如an+2=pan+1+qan(其中p2+4q≥0)的递推数列.

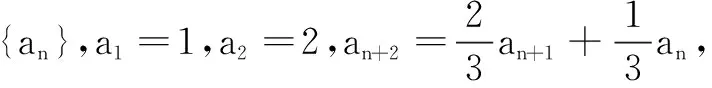
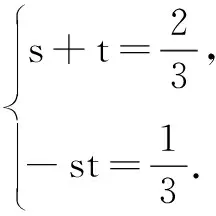
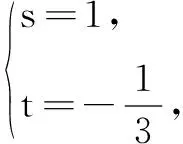
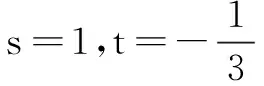
①

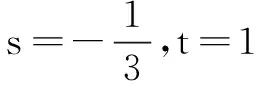
②

由① ② 可得

除了待定系数法以外,解决递推数列通项公式的方法还有:累加(乘)法、分解因式法、取倒(对)数法、换元法、归纳猜想法、迭代法等.限于篇幅,这里不再一一赘述.