探源头活水 究问题本质——以圆锥曲线中利用相关点法探求直线的斜率问题为例

朱丽娟

(江苏省扬州大学附属中学东部分校，225002)

对近几年各地的考题研究发现，解析几何的考查多以直线和圆锥曲线的位置关系的方式呈现,斜率问题是高频考题．其中一类解决斜率问题的方法就是相关点法．笔者通过这个专题的研究,试图立足基础,探索解析几何教学的良好途径,也尝试探索培养学生核心素养的方式.

一、教材探源及拓展

1.教材探源

苏教版教材选修2-1(2005年6月版)教科书《数学》第27页例2:将圆x2+y2=4上的点横坐标保持不变，纵坐标变为原来的一半，求所得曲线的方程，并说明它是什么曲线.

分析(1)只要求所得曲线上任意一点的坐标满足的方程即可;(2)将圆上点的横坐标保持不变,纵坐标变为原来的一半通过构建已知点和所求点之间的桥梁,求得方程．

解设所得曲线上任一点坐标为(x,y)，圆x2+y2=4上的对应点的坐标为(x′,y′)，

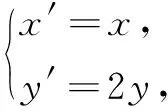
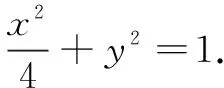
这就是变换后所得曲线的方程，它表示一个椭圆.

点评如图1,建立相关点P，D坐标关系,即建立从已知到未知的桥梁，这就是相关点法的运用,也叫坐标转移法.

2.习题拓展

课本第33页习题12:椭圆可视为对圆上的点向同一条直径施行伸缩变换而成.运用椭圆与圆之间的这种关系,你能根据圆的面积公式来猜想椭圆的面积公式吗?

点评这道题需要从椭圆的形成过程出发,类比推出椭圆的面积公式.

3.一个结论

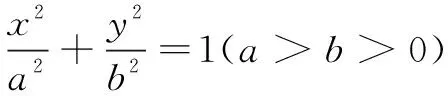
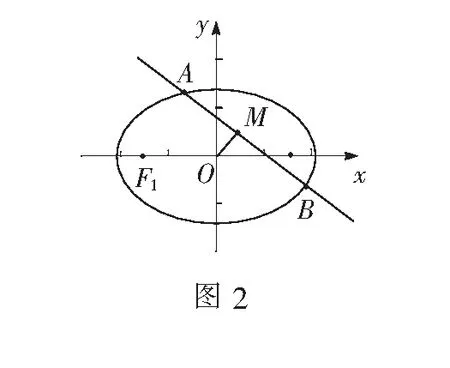
证明因为点M是弦AB的中点,所以

又A，B都在椭圆上，所以

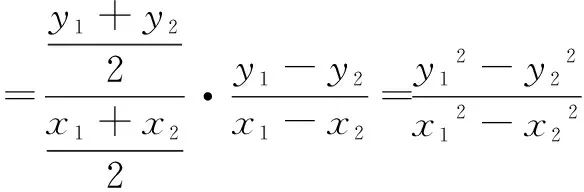
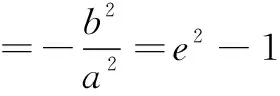
点评这是圆锥曲线中最常见的结论之一,应用也非常广泛．其中值为e2-1的形式也适用双曲线.这里相关点增加3个:A，B和中点M,由中点公式建立三者之间的关联.

二、例说相关点法探究直线的斜率问题

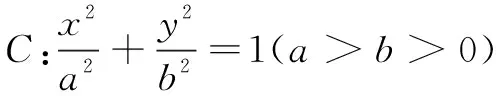
(1)求椭圆C的标准方程;

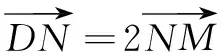
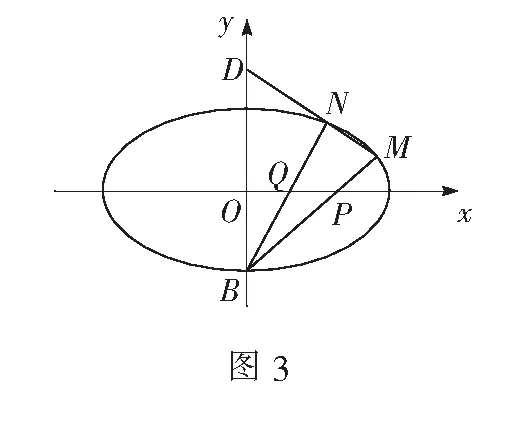
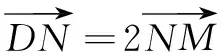
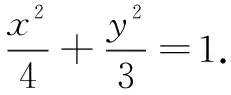
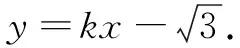
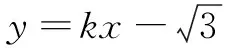
所以直线BN的斜率

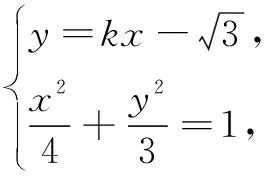
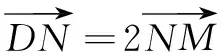
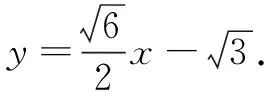
解法2设点M,N的坐标分别为(x1,y1),(x2,y2).直线BM的方程为

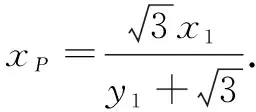
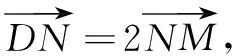
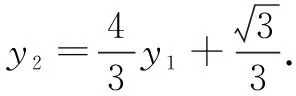
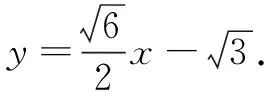
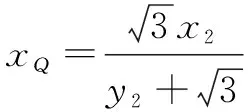
例2已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为______.

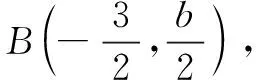
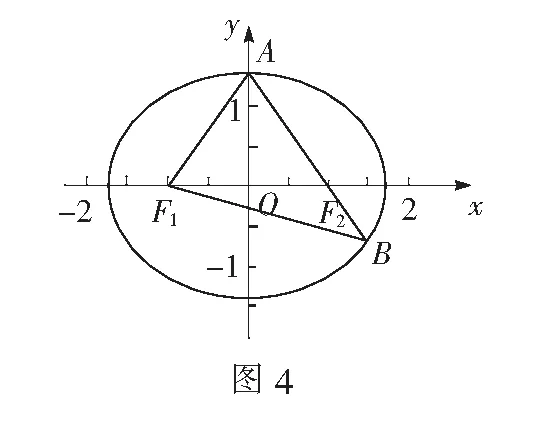
点评本题抓住了∆AF1F2的等腰特征,利用图形的几何特征解题,比较简便.解题中的图形的识别和使用,也是发展学生几何直观素养的方法.

三、反思和建议

1.注重问题的归类和寻根

注重归类就是要总结解决一类问题的通性通法,所谓考试就是练习,就是平时解题的表现．如用相关点法探究斜率问题的关键是相关点的坐标析出和表达.相关点信息的表达也许方式多元,但解题的一般算法是大同小异的.

寻根指的是题目的来源在哪里,或者说算法从哪里来,又是如何由由简单的问题变化而来等,也就是注意寻找“源头活水”.

教学中,对于新知识的学习应重视概念理解,凸显核心概念的多重表征．从数学解题的视角看,数学解题能力是一种技能，技能训练必须遵循其规律.技能训练一般有如下几个阶段:一是熟悉规则,二是熟练化,三是自动化,四是策略化.在解析几何教学中,教师应注意引导学生关注解析几何运算中的策略选择和优化,让学生提高解题能力,发展核心素养．

2.关注学生的学,才能更好地教

学生素养的形成和发展,都蕴含在学习体验中.以运算素养发展为例,包括运算对象的选择,算法的比较,过程的监控,解题后的反思等.让学生暴露思维,教师再进行认知及元认知知识、技能的指导都是必要的．美国匈菲尔德的研究表明:学生在问题解决时之所以失败,常常不是因为缺乏相关知识和认知策略,而是对认知策略的无效利用．一些教学实验也表明:数学教师可以帮助学生有效地使用问题解决策略．当然,学生运算素养的形成不是一蹴而就的,需要其自身的积累和坚持,还有非智力因素的参与.

3.立足基础,加深对解析几何本质的理解

2017年版课标指出:通过解析几何的学习,让学生感受数与形的结合,也感悟数学知识之间的关联,加强对数学整体性的理解.解题中就应体现几何和代数的有机结合,体现以坐标为桥梁,用代数的知识来研究几何问题的实质．因此,教学中引导学生抓住图形属性，理解定义本质，依靠方程工具就是解决问题的良策.