想其所想 授其所缺——高三一轮复习课“基本不等式”的教学设计与实践

凌 敏

(江苏省南京市第九中学，210000)

学生经历了高一高二阶段的系统性学习,对高中数学的基本概念和相关题型都较为熟悉,容易步入一种误区:以为自己什么都懂了，然而,一做题又是各种错误．因此，一轮复习课的重要任务之一就是纠正学生错误的认识和错误的解题方法．相较于高一高二的复习课,一轮复习课更注重方法的总结,一题多解和多题一解同样重要．下面就以“基本不等式”为例,谈谈一轮复习课的教学设计和课堂实践．

一、分析外部环境,诊断问题

二、解决问题

1. 关于“一正、二定、三相等”

(1)为什么要是正数?一定要是正数吗?不是正数可以吗?

题1判断命题“log2x+logx2的最小值是2”的真假．

设置意图旨在说明所研究的两个对象是正数还是负数,对研究结果是取最大还是最小值有影响．

(2)为什么要是定值?不是定值可以吗?

在教学实践中,我们经常会遇到学生这样的解法，也不管是不是定值,反正都令它们相等,得到最值．这样的错误很典型,有时我们向学生解释了半天,倒不如举个实例来得有效．

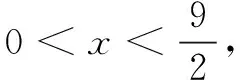
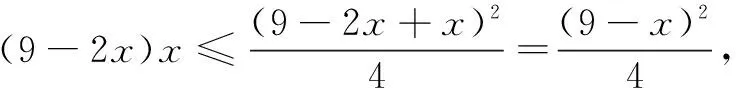
(3)相等为什么要写?不写可以吗?

经常有学生求完最值后不写取等条件,要想改掉这个不好的习惯,与其对学生说教一百遍,不如告诉他们为什么要写．

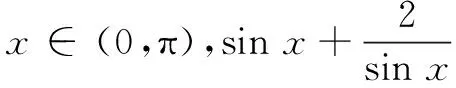
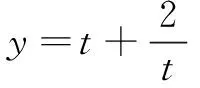
2.“解题方法多样,灵活多变,摸不着头脑”怎么办?

常有学生觉得基本不等式技巧性太强,脑袋瓜转不过来,上一题的方法在下一题中就不能用．产生这样感觉的原因或许是越是技巧方法学得多,越是抓不住问题的实质,花样太多忘了本质．查阅基本不等式解法的相关文章,在百度搜索引擎中输入“基本不等式的解法”,跳出上百万个词条,随意点开其中一篇,整理出的方法不下十几种．笔者不禁思考:真的要教给学生这么多方法吗?他们真的都能掌握吗?我们一边喊着“减负增效”,一边又硬塞给学生远超他们能力范围的东西,这是不是和我们教育的初衷背道而驰呢?思索再三,笔者依据变量个数进行分类,整理了这样几种类型和解法:

(1)单变量问题

主要方法有:直接应用、配凑法(拆项、凑项、凑系数)

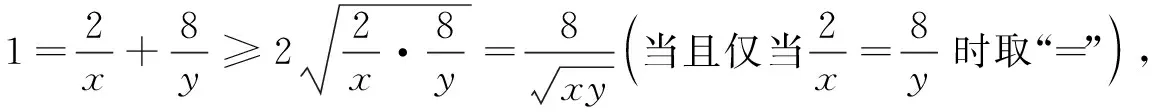
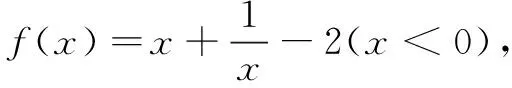
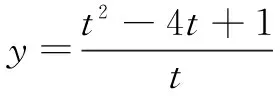
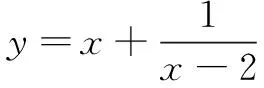
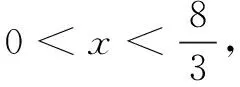
(2)双变量问题

主要方法有:直接应用、代“1”法、消元化归为单变量问题

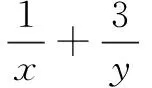
题12已知a>0,b>0,a+4b=ab,则ab的最小值是______,a+2b的最小值是______.(消元后化归为单变量问题)

设置意图笔者在教学实践中,经常遇到学生硬着头皮想要构造基本不等式的形式,尝试了很久却屡不成功的案例．在这种情形下,回归到最初的方法未尝不是一个好办法．处理二元变量问题的基本方法是消元,那么本题中的两个问题,我们都可以利用条件,得到a与b的关系,任意消去一个变量,从而使所求问题化归为单变量问题．

(3)多变量问题(主要针对三元变量问题)

主要方法:消元后转化为二元变量问题处理

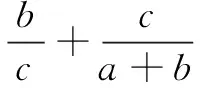
三、教师的自我总结与反思

我们提倡以“学生为主体教师为主导”的课堂教学模式,目的是希望我们的授课对象能融入知识的探索和发现过程．一轮复习课的内容,对学生来说就像一盘冷饭,如何能炒的香,让学生感受到日久弥新的新鲜感,的确是需要我们静下心来思考的问题．学生已经熟练掌握的,我们少说；学生搞不清楚的,不熟练的,还存有疑问的地方,我们多讲．所谓“师者传道授业解惑”,只有传道授业是不够的,学了知识没有疑惑也是不可能的．要让学生有疑惑说出来，和同学和老师一起分享，一起解惑,在探讨的过程中对概念认识作补偿,对知识体系作完善,对方法运用作提升,一个螺旋式的发展过程从而最终形成．