习题变式在初中几何教学中的应用研究

王晓强

[摘  要] 变式教学，是一种教师以一道典型的习题为基础，通过变化习题来引导学生逐步拓展知识、培养思维水平、提升解题技能的教学方法. 现借助几何教学中，开展习题变式教学的实例说明这样的教学方法是如何实施的.

[关键词] 习题变式;变式教学;几何

习题变式教学，是指在设计了一道习题，引导学生完成习题以后，在不改变原题本质的基础上，对问题进行延伸，比如更改一个已知条件、更改未知答案、或者把问题抽象化等，在原题的基础上延伸出数道习题，让学生通过回答一系列的习题来深入理解数学问题、培养思维水平、提升解题技能的教学活动.

应用基本的问题，帮助学生打好数学基础

教师开展变式教学，设计第一个问题的要点，是要为学生优选数学问题，帮助学生打好数学基础. 打好数学基础的内容包括帮助学生回顾一个知识概念、让学生了解正确的解题流程、能够分析出某一类问题解题的重点和难点. 教师可以应用以下的教学方法达到这样的教学效果.

第一步，教师必须为学生优选数学案例，这一数学案例中的知识点必须有典型性、延伸性、基础性.

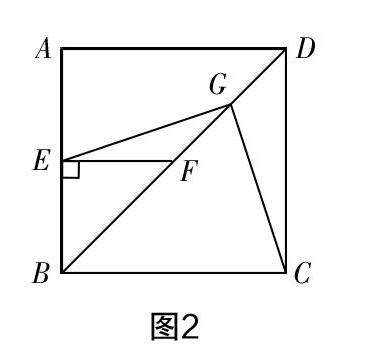
变式1：已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG. （1）求证：EG=CG.

该题具有三个特点：考核的概念具有典型性的特点，只要学生熟悉直角三角形、三角形的中线、角平分线、边、高这些概念，就能够应用数学知识解题;考核的内容具有延伸性的特点，该题中涉及的几何图形包括正方形、直角三角形等一系列几何图形，图形和图形之间联系十分紧密，教师在开展教学的时候，只要更改一个条件，整个几何图形的已知条件都会发生变化，设计这样的问题，能够让后续的几何变式教学顺利开展;题目的起点具有基础性的特点，该题的第一个数学问题并不复杂，即使是学困生，通过阅读课本，也能找到相应的数学概念来解题，这是一个能够面向所有学生，鼓励所有学生探索的数学习题.

第二步，引导学生掌握正确的解题流程.

一名学生的解题流程如下：绘制出图形如图1，证明：在Rt△FCD中，因为G为DF的中点，所以CG=FD. 同理，在Rt△DEF中，EG=FD，所以CG=EG.

学生在解题时，教师要引导学生检查他的证明流程是否存在逻辑漏洞. 如果学生在证明时出现了逻辑错误，便要反思如何应用正确的逻辑来分析问题. 教师这样开展教学的目的有两个：培养学生的解题技能及帮助学生夯实数学基础. 变式教学的后续问题会较为复杂，如果学生在基础问题的学习中就出现了解题技能不足的问题，那么在解决后续的问题中会出现更多的解题漏洞，教师做好这一环节的教学引导，能为后续的教学打好基础.

第三步，引导学生发现数学问题中的重点和难点.

教师要引导学生看到，基础习题的解题难点是什么. 教师帮助学生回顾知识点的目的是为了帮助学生积累基础变式中需要掌握的知识，后续延伸的变式都将要应用到这些基础知识.

在这一次的几何变式教学中，教师要引导学生以完成基础变式的学习来验证其是否熟悉了与直角三角形有关的概念知识，是否了解相关的数学性质等. 教师可引导学生应用思维图形、概念图、表格等，让学生梳理出相关的知识，形成完善的知识体系. 有一名学生应用表格的方式整理出了直角三角形的性质，如表1，当学生应用表格整理出直角三角性的性质，并熟悉了相关内容以后，便能迅速地突破学习重点和难点，理解第一个变式习题的解题机理.

[性质 性质呈现内容 直角三角形的两个锐角互余 如果∠C为直角，那么∠A+∠B=90° 直角三角形斜边中线性质 直角三角形斜边的中線长度为斜边的一半 直角三角形三边的关系性质 勾股定理：a2+b2=c2 直角三角形的边与角关系性质 ∠30°对应的直角边等于斜边的一半 ][表1]

应用问题的变化，帮助学生培养思维水平

教师开展变式教学，设计第二个问题的要点，在于全面地培养学生的思维水平. 教师要引导学生看到学习知识、解答习题的目的不仅是为了完成一个习题、获得一个答案. 学生在解答习题的时候，要学会充分挖掘问题，然后在解决问题的过程中，培养自己的思维水平. 教师可以应用以下的教学方法达到这样的教学目的.

第一步，教师要引导学生了解他们是学习的主体，不能被动地做习题，成为学习数学知识的机器. 学生必须要思考一个习题可以产生怎样的变化，产生探究知识的心理.

变式2：（2）将图1中△BEF绕B点逆时针旋转45°，参看图1，取DF中点G，连接EG，CG. 求证：EG=CG.

在传统的数学习题教学中，学生需要解决的是一个封闭化的数学问题，只需要根据已知条件来分析未知答案，找到问题的答案，便完成了学习任务. 在习题变式教学中，教师可以通过给出变式2，让学生意识到，虽然教师给出的变式1这个数学习题是封闭式的问题，但是学生可以根据自己的解题需求来让习题产生变化，把封闭式的问题变成开放式的问题. 教师应用这样的方法，可以激发学生主体性，使学生意识到在学习时要应用发散思维来联想问题. 教师让学生应用发散思维来思考问题，可为继续开展变式教学打好思维基础.

第二步，教师要引导学生了解数学问题可以怎样变化.

教师要通过变式训练，让学生了解数学问题可以产生怎样的变化. 比如在这一次的几何变式教学中，教师可以引导学生看到几何是研究空间结构及性质的一门学科. 学生在探究几何问题时，要应用平移、旋转、拉伸等方式来让几何图形产生变化，学生需要思考当几何图形产生变化后，它的已知条件会发生什么变化，当已知条件变化以后，未知的答案是不是会产生变化.

第三步，教师要引导学生拓展知识，让学生把知识点与知识点联系起来，解决更复杂的数学问题.

比如变式2中，几何图形发生变化以后，教师要引导学生发现仅依据原先掌握的直角三角形性质的知识，是不能解决变式2中的数学问题的，那么要解决变式2中的数学问题，需要应用到什么数学概念及数学性质？有一名学生应用了相似三角形及矩形的知识，学生的解题过程如下：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点，在△DAG与△DCG中，因为AD=CD，∠ADG=∠CDG，DG=DG，所以△DAG≌△DCG，所以AG=CG. 在△DMG与△FNG中，因为∠DGM=∠FGN，DG=FG，∠MDG=∠NFG，所以△DMG≌△FNG，所以MG=NG. 在矩形AENM中，AM=EN，在Rt△AMG与Rt△ENG中，因为AM=EN，MG=NG，所以△AMG≌△ENG，所以AG=EG，所以EG=CG. 当学生应用这样的方法解决问题以后，教师引导学生依照梳理变式1中知识体系的方法来梳理变式2中涉及的知识，帮助学生形成更为完善的知识体系.

应用问题的延伸，帮助学生养成探究习惯

教师开展变式教学，设计第三个问题的要点，是要引导学生学会自己延伸问题，养成探究的習惯. 教师要让学生意识到自己是学习的主体，必须学会自己延伸问题，找到需要研究的目标. 学生只有学会结合自己的学习兴趣、层次、需求，自己延伸问题，尽可能让习题产生变化，才能在解题的过程中学习到更多知识.

变式3：（3）将图1中△BEF绕B点旋转任意角度，参看图3，再连接相应的线段，求证：EG=CG.

变式3是教师引导学生自己思考以后设计出来的问题. 教师要引导学生把握住设计问题的几个原则：学生是否充分发挥了自己的想象力，并且联系更多知识点，设计出更多的问题. 比如在这一次的学习中，学生不仅设计出了变式3这样的问题，还考虑过将变式1中的正方形改成长方形、菱形、平行四边形等. 教师要让学生养成开放的学习心态，尽可能在探索问题的过程中吸收更多的知识，比如学生在延伸问题的过程中希望了解，如果变换了条件，那么原本题目中预设的数学关系是否还存在，如果依然存在，证明的依据是什么，可以应用什么数学思想来完成证明等. 教师要引导学生在学习变式问题时，逐步拓展知识，完善知识体系.

初中数学教学中可以在几何教学板块开展习题变式教学，只要教师把握住变式教学开展的要点，就能够帮助学生积累知识、培养学生的思维能力、锻炼学生解决问题的能力.