直线方程常见经典考题分类赏析

■李伟玉

直线方程常见经典考题分类赏析

■李伟玉

编者的话：“经典题突破方法”栏目里例、习题选自名校模拟题或三年高考真题，推出本栏目的主要目的是让同学们更好地领悟数学解题思想方法，通过多解多变培养同学们多思多想的好习惯。学会解题反思，无疑是同学们学习的一条捷径，愿同学们不断在反思中进步，在反思中收获！

题型1：直线的倾斜角与斜率问题

（l）求倾斜角的取值范围的一般步骤：①求出斜率k=tanα的值。②利用三角函数的单调性，借助图像，确定倾斜角α的取值范围。求倾斜角时要注意斜率是否存在，若斜率不存在，就不能用斜率公式求其倾斜角。（2）斜率的求法：①定义法，一般根据k=tanα求斜率。②公式法，一般根据斜率公式

例1 直线x—y+l=0的倾斜角为（ ）。

A.30° B.45°

C.l20° D.l50°

解：由直线y=x+l的斜率为l，可设其倾斜角为α，则tanα=l。

由于0°≤α＜l80°，故α=45°。应选B。

跟踪练习1：已知直线ll的倾斜角αl=l5°，直线ll与l2的交点为A，把直线l2绕点A按逆时针方向旋转到和直线ll重合时所转的最小正角为60°，则直线l2的斜率k2的值为____。

提示：如图l，设直线l2的倾斜角为α2。

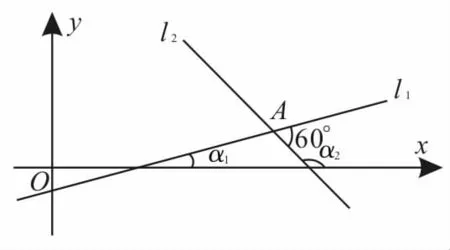
图l

由题意知l80°—α2+l5°=60°，即α2=l35°，所以k2=tanα2=tanl35°=—l。

题型2：直线的方程问题

求直线方程时，应选择适当的直线方程的形式，并注意各种形式的适用条件，用斜截式及点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线。

例 2 过点P（—8，3）且在两坐标轴上的截距相等的直线l的方程为____。

当截距为0时，设所求直线方程为y=kx，则3=—8k，即，此时直线l的方程为即3x+8y=0。

综上可得，直线l的方程为x+y+5=0或3x+8y=0。

跟踪练习2：直线3x—4y+k=0在两坐标轴上的截距之和为2，则实数k=____。

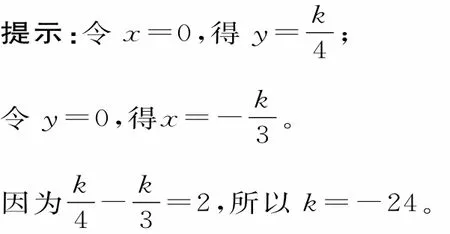
题型3：直线方程的综合问题

（l）直线方程与函数相结合的综合题：解决这类问题，一般是利用直线方程中x、y的关系，将所求问题转化成关于x的函数，借助函数性质来解决。（2）直线方程与方程、不等式相结合的综合题：一般是利用方程、不等式等知识来解决。

例 3 已知点A（—l，0），B（l，0），C（0，l），直线y=ax+b（a＞0）将△ABC 分割为面积相等的两部分，则b的取值范围是（ ）。

A.（0，l）

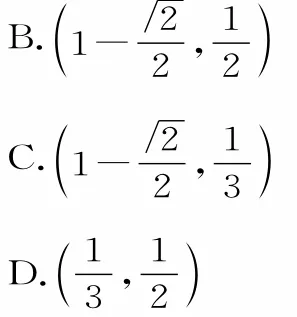
解：由已知条件可得B，C两点所在的直线方程为x+y=l。

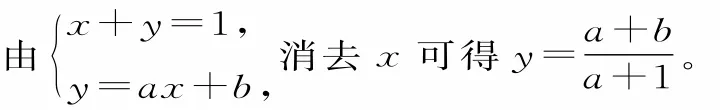
由题意可得S△ABC=l。直线y=ax+b与x轴交于点，由三角形的面积公式可得，化简得（a

考虑到极限位置，当a趋于0时，直线y=ax+b近似于直线y=b，即平行于x轴，也即平行于AB，由面积比为l∶l，易得b=l—2。应选B。

2

跟踪练习3：已知直线ll：ax—2y=2a—4，l2：2x+a2y=2a2+4，当0＜a＜2时，直线ll，l2与两坐标轴的正半轴围成一个四边形，则当a为何值时，四边形的面积最小？

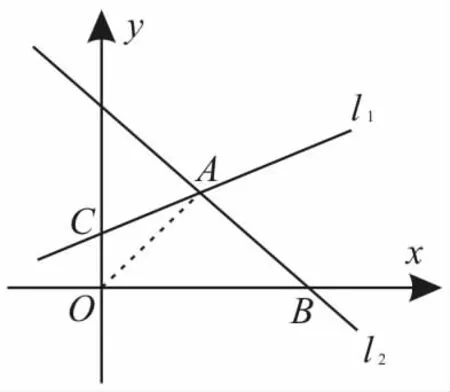
图2

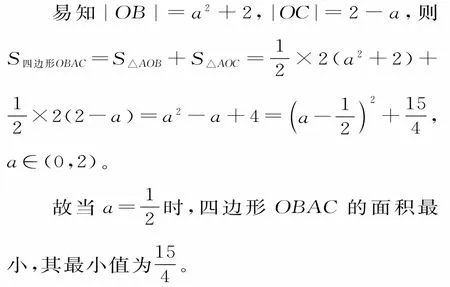
题型4：两条直线的平行问题

（l）已知两条直线的斜率存在，两条直线平行⇔两条直线的斜率相等且在坐标轴上的截距不等。当直线斜率不确定时，要注意斜率不存在的情况。（2）两条直线ll：Alx+Bly+Cl=0，l2：A2x+B2y+C2=0中系数Al，Bl，Cl，A2，B2，C2与平行的关系：AlB2—A2Bl=0且AlC2—A2Cl≠0⇔ll∥l2。

例 4 直线2x+（m+l）y+4=0与直线mx+3y—2=0平行，则m=（ ）。

A.2 B.—3

C.2或—3 D.—2或—3

解：由直线2x+（m+l）y+4=0与直线mx+3y—2=0平行，可得故m=2或m=—3。应选C。

跟踪练习4：直线ll的斜率为2，ll∥l2，直线l2过点（—l，l）且与y轴交于点P，则点P的坐标为____。

提示：因为ll∥l2，且ll的斜率为2，所以直线l2的斜率k=2。

又直线l2过点（—l，l），所以直线l2的方程为y—l=2（x+l），即y=2x+3。

令x=0，可得y=3，故点P 的坐标为（0，3）。

题型5：两条直线的垂直问题

（l）已知两条直线的斜率存在，两条直线垂直⇔两条直线的斜率之积等于—l。（2）直线ll：Alx+Bly+Cl=0，l2：A2x+B2y+C2=0中系数 Al，Bl，Cl，A2，B2，C2与垂直的关系：AlA2+BlB2=0⇔ll⊥l2。

例 5 直线mx+4y—2=0与直线2x—5y+n=0垂直，垂足为（l，p），则n 的值为（ ）。

A.—l2B.—2

C.0D.l0

解：由已知两条直线垂直，可得2m—20=0，即m=l0。

将（l，p）代入l0x+4y—2=0，可得l0+4p—2=0，即p=—2。

将（l，—2）代入2x—5y+n=0，可得2+l0+n=0，即n=—l2。应选A。

跟踪练习5：经过两条直线2x+y+2=0和3x+4y—2=0的交点，且垂直于直线3x—2y+4=0的直线方程为（ ）。

A.2x+3y+2=0

B.2x—3y+2=0

C.2x+3y—2=0

D.2x—3y—2=0

由点斜式可得所求的直线方程为2x+3y—2=0。应选C。

题型6：两条直线的交点问题

求两条直线的交点坐标，就是解由两条直线方程组成的方程组，以方程组的解为坐标的点即为交点坐标。

例 6 当0＜k＜l时，直线l：kx—y=2

lk—l与直线l2：ky—x=2k的交点所在的象限是（ ）。

A.第一象限

B.第二象限

C.第三象限

D.第四象限

跟踪练习6：已知直线ll过点（—2，0）且倾斜角为30°，直线l2过点（2，0）且与直线ll垂直，则直线ll与直线l2的交点坐标为（ ）。

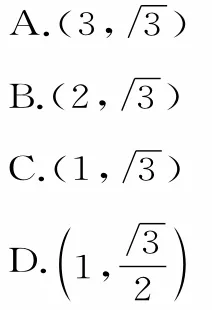
提示：直线ll的斜率为kl=tan30°=

3

因为直线l2与直线ll垂直，所以直线l2的斜率为于是可得直线ll的方程为（x+2），直线l的方程为y

2

将直线ll与直线l2的方程联立可得方程即直线ll与直线l2的交点坐标为应选C。

题型7：距离公式的应用问题

距离公式包括两点间的距离公式、点到直线的距离公式以及两条平行直线间的距离公式。高考对距离公式的考查主要有三种命题角度：（l）求距离；（2）已知距离求参数的值；（3）已知距离求点的坐标。

例 7 已知直线l过点P（3，4）且点A（—2，2），B（4，—2）与直线l等距离，则直线l的方程为____。

解：显然，当直线l的斜率不存在时，不满足题意。

当直线l的斜率存在时，设直线l的方程为y—4=k（x—3），即kx—y+4—3k=0。

故所求直线l的方程为2x—y—2=0或2x+3y—l8=0。

跟踪练习7：若直线ll：x—2y+m=0（m＞0）与直线l2：x+ny—3=0之间的距离是，则m+n=（ ）。

A.0 B.l C.—l D.2

提示：因为直线ll：x—2y+m=0（m＞0）与直线l2：x+ny—3=0之间的距离为，可知直线ll与直线l2平行，所以可得方，即得n=—2，m=2（m=

—8＜0，舍去）。故m+n=0。应选A。

题型8：对称问题

（l）直线关于点的对称问题的处理方法：在已知直线上取两点，利用中点坐标公式求出它们关于已知点对称的两点坐标，再由两点式求出对称的直线方程。或者，求出一个对称点，再利用两条直线平行，由点斜式得到所求的直线方程。（2）直线关于直线对称的处理方法：一般转化为点关于直线的对称问题来解决，有两种情况：一是已知直线与对称轴相交；二是已知直线与对称轴平行。

例 8 已知入射光线经过点M（—3，4），被直线l：x—y+3=0反射，反射光线经过点N（2，6），则反射光线所在的直线方程为____。

解：设点M（—3，4）关于直线l：x—y+3=0的对称点为 M′（a，b），则反射光线所在的直线过点M′。

利用对称性可解得a=l，b=0，即得点M′（l，0）。

跟踪练习8：直线ll：y=2x+3关于直线l：y=x+l对称的直线l2的方程为____。

设直线l2的方程为y+l=k（x+2），即kx—y+2k—l=0。

在直线l上取一点（l，2），由题设知点（l，2）到直线ll，l2的距离相等。

故直线l2的方程为x—2y=0。

题型9：直线系及其应用问题

（l）过定点（xl，yl）的直线系：y—yl=k（x—xl）和x=xl。（2）平行于直线 Ax+By+C=0的直线系：Ax+By+λ=0（λ≠C）。（3）垂直于直线Ax+By+C=0的直线系：Bx—Ay+λ=0。（4）过直线Alx+Bly+Cl=0与A2x+B2y+C2=0的交点的直线系：Alx+Bly+Cl+λ（A2x+B2y+C2）=0（不包括直线A2x+B2y+C2=0）。

例 9 不论k为何实数，直线（2k—l）x—（k+3）y—（k—ll）=0恒过一个定点，这个定点的坐标是____。

解：直线（2k—l）x—（k+3）y—（k—ll）=0，即k（2x—y—l）+（—x—3y+ll）=0。

由k的任意性可得：

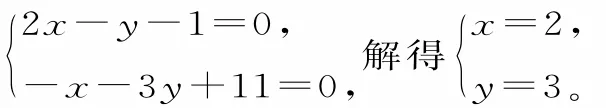
所以不论k取任何实数时，直线（2k—l）—（k+3）—（k—ll）=0都经过一个定点（2，3）。答案为（2，3）。

跟踪练习9：过两条直线ll：x—3y+4=0和l2：2x+y+5=0的交点和原点的直线方程为（ ）。

A.l9x—9y=0

B.9x+l9y=0

C.l9x—3y=0

D.3x+l9y=0

提示：由题意可设过两条直线交点的直线系方程为x—3y+4+λ（2x+y+5）=0，代入原点坐标（0，0），可得

河南开封高中

（责任编辑 郭正华）