聚焦圆的最值的交汇问题

■宋全会 赵 昆

聚焦圆的最值的交汇问题

■宋全会 赵 昆

圆是高中解析几何的重要内容，圆的最值问题又是高考考查的重点内容，且常常和高中数学的其他知识交汇考查。下面就圆的最值的交汇问题，进行分类解析，以加深同学们对此类问题的理解与应用。

一、圆与定点的交汇问题

1.圆外一定点到圆上一动点距离的最大值与最小值问题

例 1 已知点M（—l，2），点N 在圆C：（x—2）2+y2=9上，求的最大值和最小值。

解：由圆C：（x—2）2+y2=9，可知圆心C2，0（），半径R=3。

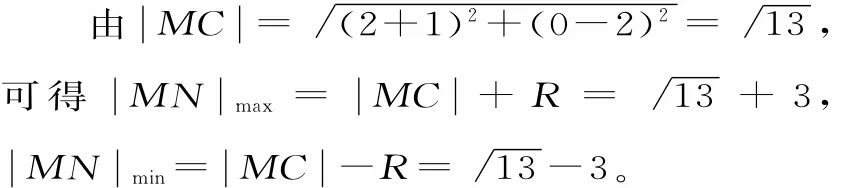
方法归纳：设圆外一点M 到圆心为C、半径为R的圆上的点N的距离为d，则dmin

如图l，过点P的直线AB⊥PC，其中A，B是直线与圆的交点，则线段AB即为所求的最短弦。

由于△APC为直角三角形，且|AC|=R=2，|PC|=

图l

2.过圆内一定点的最长弦和最短弦问题

例 2 已知点P（0，l）在圆C：（x—l）2+y2=4的内部，则过点P的直线被圆截得的最长弦与最短弦分别为____。

解：依题意可得，最长弦为圆的直径，即弦长为4。

方法归纳：经过圆内的点且过圆心的弦即为最长弦（直径），与最长弦垂直的弦是最短弦。

二、圆与直线的交汇问题

1.圆上的动点到定直线的距离的最大值和最小值问题

例 3 圆C：x2+y2—2x—2y+l=0上的动点M 到直线x—y—2=0的距离的最大值是（ ）。

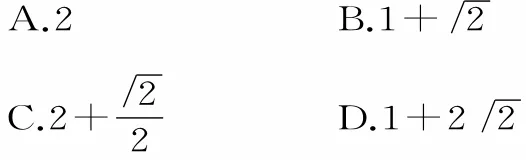
解：圆x2+y2—2x—2y+l=0的圆心C（l，l），半径R=l，则圆心C到直线x—y—2=0的距离

故圆x2+y2—2x—2y+l=0上的动点M 到直线x—y—2=0的距离的最大值为d+R =l+。应选B。

方法归纳：若C为一定点，P是一条直线上的动点，则 PC 的最小值就是定点C到该直线的距离。

2.过定直线上的动点作圆的切线，求切线长的最小值问题

例4 过直线y=x+l上的任一点向圆C：（x—3）2+y2=l引切线，则切线长的最小值为（ ）。

解：如图2所示。设直线上的任一点为P，切点为Q。由题意可知圆心为C（3，0）。

由PQ为切线，可知 PQ⊥CQ，|CQ|=R=l，可得切线长|PQ|=所以当|PC|的值最小时，|PQ|取得最小值。

图2

由题意可知，|PC|的最小值为圆心C到直线y=x+l的距离，所以

方法归纳：|PC|的最小值即为圆心到直线的距离，因此可借助点到直线的距离公式求得。

三、圆与圆的交汇问题

1.两圆上动点的距离的最大值与最小值问题

例 5 点P 在圆Cl：x2+y2—8x—4y+ll=0上，点Q 在圆C2：x2+y2+4x+2y+l=0上，则的最小值为（ ）。

解：圆Cl：x2+y2—8x—4y+ll=0的方程可化为（x—4）2+（y—2）2=9，所以圆Cl的圆心Cl（4，2），半径Rl=3；圆C2：x2+y2+4x+2y+l=0的方程可化为（x+2）2+（y+l）2=4，所以圆C2的圆心C2（—2，—l），半径R2=2。

方法归纳：圆Cl的半径为Rl，圆C2的半径为R2，圆Cl上的动点为M，圆C2上的动点为N，则

2.直线上的点到两圆上的点的距离的最值问题

例6 已知M，N分别为圆Cl：（x—4）2+（y—l）2=4与圆C2：（x+l）2+（y—2）2=l上的点，P为直线l：y=x+l上的一点，则

解：圆Cl：（x—4）2+（y—l）2=4的圆心Cl（4，l），半径Rl=2；圆C2：（x+l）2+（y—2）2=l的圆心C2（—l，2），半径R2=l。

由圆心Cl，C2的坐标可知，Cl，C2位于直线l：x—y+l=0的两侧，如图3所示。

设圆心C2关于直线l：x—y+l=0的对称点为C3（x0，y0），则由对称性可得方程组

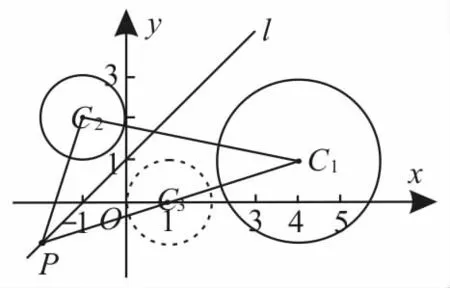
图3

所以圆C2关于直线l：x—y+l=0的对称圆C3的圆心为C3（l，0），半径R3=l。由对称性可知

方法归纳：解决此类问题，首先要判断两点在已知直线“同侧”还是“异侧”，根据需要求其中一个点关于已知直线的对称点，然后利用“同侧和最小，异侧差最大”求解。

四、与圆上点的坐标有关的交汇问题

例 7 已知点P（x，y）在圆x2+（y—l）2=l上运动，则的最大值与最小值分别为____。

点Q（2，l）连线的斜率。

所求问题可转化为过定点Q（2，l）的动直线与圆有交点的情况下，求斜率k的最大值和最小值。根据圆的几何意义知，当该直线与圆相切时，k取得最大值与最小值。

设过定点Q（2，l）的直线方程为y—l=k（x—2），即kx—y+l—2k=0。

2.形如z=ax+by的最值问题

例 8 已知实数x，y满足方程x2+y2—4x+l=0，求y—x的最大值和最小值。

解：令z=y—x，则z看作是直线y=x+z在y轴上的截距。

已知方程x2+y2—4x+l=0为圆的方程，其圆心坐标为（2，0），半径R=3。

当直线y=x+z与圆相切时，截距z取得最大值和最小值。由

方法归纳：形如z=ax+by的最值问题，可转化为直线在y轴上的截距的最值问题。根据圆的几何意义知，当直线与圆相切时，直线在y轴上的截距取得最大值和最小值。

3.形如D=（x—a）2+（y—b）2的最值问题

例 9 已知函数y=f（x）是定义在R上的增函数，函数y=f（x—l）的图像关于点（l，0）对称。若对任意的x，y∈R，不等式f（x2—6x+2l）+f（y2—8y）＜0恒成立，则当x＞3时，x2+y2的取值范围是（ ）。

A.（3，7） B.（9，25）

C.（l3，49） D.（9，49）

解：由函数y=f（x—l）的图像关于点（l，0）对称，可得到函数y=f（x）的图像关于点（0，0）对称，由此可知函数y=f（x）为奇函数。

因为f（x2—6x+2l）+f（y2—8y）＜0，所以f（x2—6x+2l）＜f（8y—y2）。

又因为函数y=f（x）是定义在R上的增函数，所以x2—6x+2l＜8y—y2，可得（x—3）2+（y—4）2＜4，且x＞3。

所以点（x，y）所形成的区域可看作以C（3，4）为圆心，2为半径的半圆内部，如图4所示。

根据两点间的距离公式，令D=x2+y2，则D=x2+y2可看作半圆（x—3）2+（y—4）2＜4，且x＞3的内部的点（x，y）到原点（0，0）的距离的平方。

图4

由圆的几何性质可知，当点（x，y）在半圆的B点时距离最大，即

当点（x，y）在半圆的 A（3，2）点时距离最小，即Dmin=3—0（）2+2—0（）2=l3。

由上可知，x2+y2的取值范围为（l3，49）。应选C。

附言：本文系20l6年度河南省基础教育教学研究项目《微课资源建设与应用研究》研究成果，课题编号：JCJYBl6250232。

河南开封高中

（责任编辑 郭正华）