圆的方程常见经典考题分类赏析

■毕宁远

圆的方程常见经典考题分类赏析

■毕宁远

圆是高中数学的常见图形，圆的方程是高考的常考点。在解决圆的方程问题的过程中，要体会用代数方法处理几何问题的思想。

题型1：求圆的方程问题

求圆的方程的常见方法：（l）几何法，利用圆的一些常用性质和定理求出圆的相关量。如圆心在过切点且与切线垂直的直线上，圆心在任意弦的中垂线上，两圆相切时切点与两圆心三点共线。（2）代数法，根据条件设出圆的方程，再由题目给出的条件，列出等式，求出相关量。一般地，与圆心和半径有关的问题，选择标准式，否则，选择一般式。

例 1 已知a∈R，方程a2x2+（a+2）y2+4x+8y+5a=0表示圆，则圆心坐标是____，半径是____。

解：由已知方程表示圆，可得a2=a+2，解得a=2或a=—l。

当a=2时，方程不满足表示圆的条件。

当a=—l时，原方程为x2+y2+4x+8y—5=0，化为标准方程为（x+2）2+（y+4）2=25，此方程表示以（—2，—4）为圆心，半径为5的圆。

综上可知，所求的圆心坐标为（—2，—4），半径为5。

跟踪训练1：经过点A（5，2），B（3，—2），且圆心在直线2x—y—3=0上的圆的方程为____。

提示：（法l）因为圆过 A（5，2），B（3，—2）两点，所以圆心一定在线段AB的垂直平分线上。容易求得线段AB的垂直平分线方程为y=

故所求圆的标准方程为（x—2）2+（y—l）2=l0。

（法2）设所求圆的方程为x2+y2+Dx+Ey+F=0（D2+E2—4F＞0），其圆心坐标为解此方程组可得D=—4，E=—2，F=—5。

故所求圆的一般方程为x2+y2—4x—2y—5=0。

题型2：与圆有关的最值问题

与圆有关的最值问题是高考命题的热点，其考查的重点是数形结合与转化思想的应用。

例 2 已知M 为圆C：x2+y2—4x—l4y+45=0上任意点，且点Q（—2，3）。

（l）求|MQ|的最大值和最小值。

解：由圆C：x2+y2—4x—l4y+45=0，可得（x—2）2+（y—7）2=8，所以圆心C 的坐标为（2，7），半径r=2

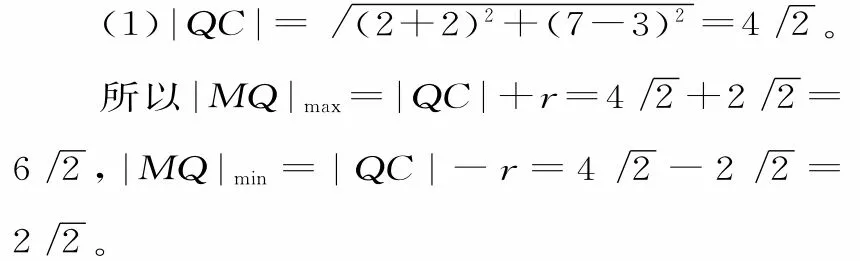
设直线MQ的方程为y—3=k（x+2），即kx—y+2k+3=0，则

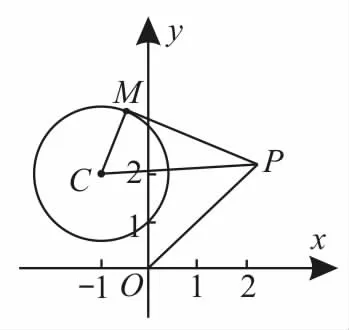
跟踪训练2：已知从圆C：（x+l）2+（y—2）2=2外一点P（xl，yl）向该圆引一条切线，切点为 M，O 为坐标原点，且有取得最小值时点P的坐标为____。

提示：如图l所示，圆C：（x+l）2+（y—2）2=2，可知圆心C（—l，2），半径

图l

当直线PO垂直于直线2x—4y+3=0，即直线PO的方程为2x+y=0时小，此时P点即为两直线的交点。容易得到P点的坐标为

题型3：与圆有关的轨迹问题

与圆有关的轨迹问题的常见解法：（l）直接法，根据题设条件列出方程求解。（2）定义法，根据圆的定义求解。（3）几何法，利用圆的性质求解。（4）代入法，找出要求点与已知点的关系，代入已知点满足的关系式求解。

例3 已知圆x2+y2=4上一定点A（2，0），B（l，l）为圆内一点，P，Q 为圆上的动点。

（l）求线段AP中点的轨迹方程。

（2）若∠PBQ=90°，求线段PQ 中点的轨迹方程。

解：（l）设AP 的中点为M（x，y）。由中点坐标公式可知，P点坐标为（2x—2，2y）。

因为P点在圆x2+y2=4上，所以（2x—2）2+（2y）2=4。

故所求线段AP中点的轨迹方程为（x—l）2+y2=l。

（2）设PQ 的中点为N（x，y）。

在Rt△PBQ中，|PN|=|BN|。

设O为坐标原点，连接ON（图略），则ON⊥PQ，所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2，可得x2+y2+（x—l）2+（y—l）2=4。

故所求线段PQ中点的轨迹方程为x2+y2—x—y—l=0。

跟踪训练3：已知直角三角形ABC的斜边为AB，且点A（—l，0），B（3，0）。

求：（l）直角顶点C的轨迹方程。

（2）直角边BC中点M 的轨迹方程。

提示：（l）（法l）设顶点C（x，y）。

因为AC⊥BC，且A，B，C三点不共线，所以x≠3且x≠—l。

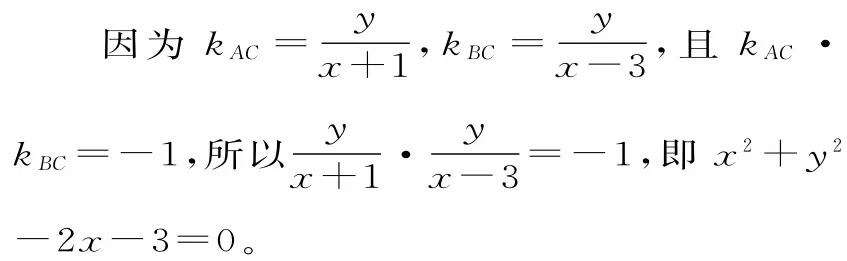
故所求直角顶点C的轨迹方程为x2+y2—2x—3=0（x≠3且x≠—l）。

（法2）设AB的中点为D。

由中点坐标公式可得点D（l，0）。

由圆的定义知，动点C的轨迹是以D（l，0）为圆心，2为半径的圆（由于A，B，C三点不共线，所以应除去与x轴的交点）。

故直角顶点C的轨迹方程为（x—l）2+y2=4（x≠3且x≠—l）。

（2）设点 M（x，y），点C（x0，y0）。

由点B（3，0），M 是线段BC的中点，利用中点坐标公式可得，即得x=2x—3，y=2y。00

由（l）知，点C 在圆（x—l）2+y2=4（x≠3且x≠—l）上运动，将x0=2x—3，y0=2y代入该方程得（2x—4）2+（2y）2=4，即（x—2）2+y2=l（x≠3且x≠—l）。

故所求动点M 的轨迹方程为（x—2）2+y2=l（x≠3且x≠—l）。

题型4：与圆有关的对称问题

（l）圆的轴对称性，即圆关于直径所在的直线对称。（2）圆关于点对称，求已知圆关于某点对称的圆，只需确定所求圆的圆心位置；两圆关于某点对称，则此点为两圆的圆心连线的中点。（3）圆关于直线对称，求已知圆关于某条直线对称的圆，只需确定所求圆的圆心位置；两圆关于某条直线对称，则此直线为两圆圆心连线的垂直平分线。

例 4 在平面直角坐标系xOy中，圆C：x2+y2+4x—2y+m=0与直线x—3y+3—2=0相切。

（l）求圆C的方程。

（2）若圆C上有两点M，N 关于直线x+2y=0对称，且|MN|=23，求直线MN 的方程。

解：（l）将圆C：x2+y2+4x—2y+m=0的方程化为圆C：（x+2）2+（y—l）2=5—

m。

因为圆C：x2+y2+4x—2y+m=0与直线相切，所以圆心（—2，l）到直线的距离

故所求圆C 的方程为（x+2）2+（y—l）2=4。

（2）若圆C上有两点M，N 关于直线x+2y=0对称，则可设直线MN的方程为2x—y+c=0。

因为|MN|=23，半径r=2，所以圆心（—2，l）到直线MN 的距离为

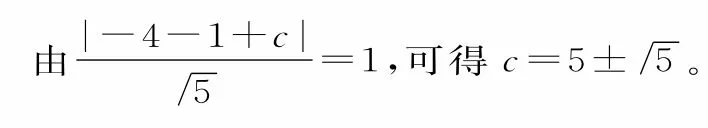
跟踪训练4：圆（x—l）2+（y—2）2=l关于直线y=x对称的圆的方程为（ ）。

A.（x—2）2+（y—l）2=l

B.（x+l）2+（y—2）2=l

C.（x+2）2+（y—l）2=l

D.（x—l）2+（y+2）2=l

提示：已知圆的圆心C（l，2）关于直线y=x对称的点为C′（2，l），所以圆（x—l）2+（y—2）2=l关于直线y=x对称的圆C′的方程为（x—2）2+（y—l）2=l。应选A。

题型5：直线与圆的位置关系问题

直线与圆的位置关系问题的处理方法：（l）几何法，利用d与r的关系求解。（2）代数法，利用判别式求解。（3）点与圆的位置关系法，利用直线恒过定点求解。

例 5 已知点 M（a，b）在圆O：x2+y2=l外，则直线ax+by=l与圆O的位置关系是（ ）。

A.相切 B.相交

C.相离 D.不确定

解：因为点 M（a，b）在圆O：x2+y2=l外，所以a2+b2＞l。

跟踪训练5：圆（x—3）2+（y—3）2=9上到直线3x+4y—ll=0的距离等于l的点的个数为（ ）。

A.l B.2 C.3 D.4

如图5所示，圆上到直线的距离为l的点有3个。应选C。

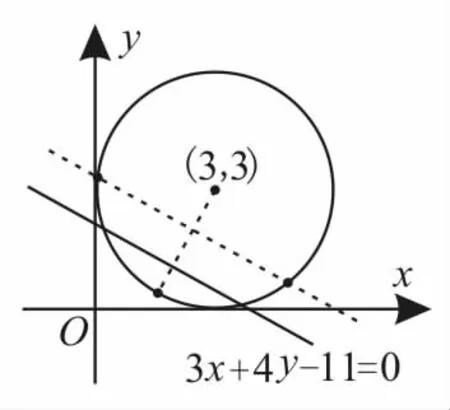
图2

题型6：圆与圆的位置关系问题

判断两圆的位置关系常用几何法，即利用两圆的圆心距与两圆半径的和与差之间的关系求解。

例 6 已知圆M：x2+y2—2ay=0（a＞0）截直线x+y=0所得线段的长是则圆M 与圆N：（x—l）2+（y—l）2=l的位置关系是（ ）。

A.内切 B.相交

C.外切 D.相离

所以圆M 的方程为x2+y2—4y=0，即x2+（y—2）2=4，其圆心坐标为 M（0，2），半径rl=2。

又因为圆 N：（x—l）2+（y—l）2=l的圆心N（l，l），半径r2=l，所以|MN|=

因为rl—r2=l，rl+r2=3，l＜|MN|＜3，所以两圆相交。应选B。

（法2）由x2+y2—2ay=0（a＞0），可得x2+（y—a）2=a2（a＞0），所以圆 M 的圆心为M（0，a），半径rl=a。

以下同法l（略）。

跟踪训练6：已知两圆的方程分别为x2+y2—2x—6y—l=0，x2+y2—l0x—l2y+m=0。

（l）m取何值时两圆外切？

（2）m取何值时两圆内切？

（3）当m=45时，求两圆的公共弦所在的直线方程和公共弦的长。

提示：因为两圆的标准方程分别为（x—l）2+（y—3）2=ll，（x—5）2+（y—6）2=6l—m，所以两圆的圆心坐标分别为（l，3），（5，

（3）由（x2+y2—2x—6y—l）—（x2+y2—l0x—l2y+45）=0，可得两圆的公共弦所在的直线方程为4x+3y—23=0。

题型7：圆的切线方程问题

求过定点的圆的切线方程时，首先要判断定点在圆上还是在圆外，若在圆上，则该点为切点，切线仅有一条；若在圆外，则切线应有两条；若用切线的点斜式方程，不要忽略斜率不存在的情况。求切线长要利用切线的性质，即过切点的半径垂直于切线。

例 7 过点（3，l）作圆（x—l）2+y2=r2的切线有且只有一条，则该切线方程为（ ）。

A.2x+y—5=0

B.2x+y—7=0

C.x—2y—5=0

D.x—2y—7=0

解：因为过点（3，l）作圆（x—l）2+y2=r2的切线有且只有一条，所以点（3，l）在圆（x—l）2+y2=r2上。

跟踪训练7：已知P（x，y）是直线kx+y+4=0（k＞0）上一点，PA 是圆C：x2+y2—2y=0的一条切线，A是切点，若PA的最小长度为2，则k的值为（ ）。A.3 B.2l 2

C.22 D.2

提示：圆C：x2+y2—2y=0的圆心为C（0，l），半径r=l。

因为PA 是圆C：x2+y2—2y=0的一条切线，A是切点，PA的最小长度为2，所以圆心到直线kx+y+4=0的距离为5。由点到直线的距离公式可

因为k＞0，所以k=2。应选D。

题型8：圆的弦长问题

例 8 已知直线l：x—3y+6=0与圆x2+y2=l2交于A，B两点，过点A，B分别作直线l的垂线与x轴交于C，D 两点，则|CD|=____。

解：（法l）由圆x2+y2=l2，可知圆心O（0，0），半径r=

如图3所示，过 C 作CE⊥BD于点E，则|CE|=|AB|=

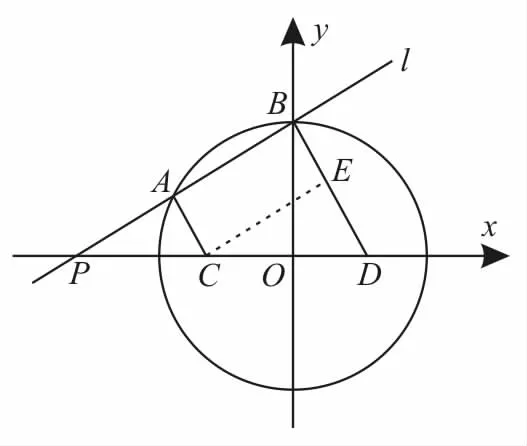
图3

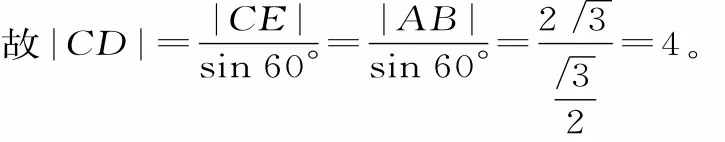
（法2）设点A（xl，yl），B（x2，y2）。

令y=0，分别得xC=—2，xD=2，所以|CD|=2—（—2）=4。

跟踪训练8：设直线y=x+2a与圆C：x2+y2—2ay—2=0相交于A，B 两点，若则圆C的面积为____。

提示：圆C：x2+y2—2ay—2=0，即圆C：x2+（y—a）2=a2+2，可知圆心坐标为C（0，a）。

题型9：圆系方程问题

具有某些共同性质的圆的集合称为圆系，它们的方程叫作圆系方程。常见的圆系方程有以下几种：①同心圆系方程：（x—a）2+（y—b）2=r2（r＞0），其中a，b 是定值，r是参数。②半径相等的圆系方程：（x—a）2+（y—b）2=r2（r＞0），其中r是定值，a，b 是参数。③过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程：x2+y2+Dx+Ey+F+λ（Ax+By+C）=0（λ∈R）。④过圆Cl：x2+y2+Dlx+Ely+Fl=0和圆C2：x2+y2+D2x+E2y+F2=0交点的圆系方程：x2+y2+Dlx+Ely+Fl+λ·（x2+y2+D2x+E2y+F2）=0（λ≠—l，其中不含圆C2），当λ=—l时，圆系方程表示直线l：（Dl—D2）x+（El—E2）y+（Fl—F2）=0。若两圆相交，则直线l为两圆相交弦所在直线；若两圆相切，则直线l为公切线。

例 9 求以相交圆Cl：x2+y2+4x+y+l=0及C2：x2+y2+2x+2y+l=0的公共弦为直径的圆的方程。

解：由两个圆的方程相减，得2x—y=0即为公共弦所在的直线方程。

显然圆C2的圆心（—l，—l）不在此直线上，故可设所求圆O的方程为x2+y2+4x+y+l+λ（x2+y2+2x+2y+l）=0（λ∈R，λ≠—l），即（l+λ）x2+（l+λ）y2+2（2+λ）x+（l+2λ）y+（l+λ）=0，其圆心O 的坐标

跟踪训练9：在以k为参数的圆系：x2+y2+2kx+（4k+l0）y+l0k+20=0中，试证两个不同的圆相内切或相外切。

提示：将原方程转化为（x+k）2+（y+2k+5）2=5（k+l）2。

题型10：圆的创新问题

创新问题是高考的命题热点，创新问题的特点是背景新颖，信息量大，通过它可考查同学们获取信息以及解决问题的能力。

例10 两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行直线和圆“相交”；若两条平行直线和圆没有公共点，则称两条平行直线和圆“相离”；若两条平行直线和圆有一个、两个或三个不同的公共点，则称两条平行直线和圆“相切”。已知直线ll：2x—y+a=0，l2：2x—y+a2+l=0和圆x2+y2+2x—4=0相切，则a的取值范围是（ ）。

A.a＞7或a＜—3

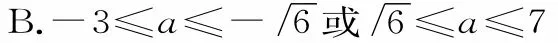
当两条平行直线和圆相切时，可把以上两种情况下求得a的范围取并集后，再取此并集的补集，即为所求。故所求a的取值范围是—3≤a≤—6或6≤a≤7。应选B。

跟踪训练10：已知函数y=f（x）（x∈R），对函数y=g（x）（x∈I），定义g（x）关于f（x）的“对称函数”为函数y=h（x）（x∈I），y=h（x）满足：对任意x∈I，两个点（x，h（x）），（x，g（x））关于点（x，f（x））对称。

提示：g（x）的图像表示圆的一部分（图略），即x2+y2=4（y≥0）。

当直线y=3x+b与半圆相切时，满足h（x）＞g（x）。

根据圆心（0，0）到直线y=3x+b的距离是圆的半径可得解得b=

浙江绍兴市上虞区春晖中学

（责任编辑 郭正华）