本期试卷参考答案与提示

本期试卷参考答案与提示

编者的话：同学们在演练的过程中，如果需要更为详细的参考答案，请扫描右边的二维码，关注编辑部的官微“高中数学解题反思”，不但能获悉详细参考答案，还可以另辟蹊径，开拓知识视野，学会解题反思！

直线与方程综合演练A卷参考答案与提示

一、选择题

1.B 2.B 3.D 4.D 5.C 6.A 7.B

8.A 9.D 10.A 11.B 12.C 13.C 14.B 15.D 16.A 17.B 提示：直线方程，由此可知两条直线的斜率同号。 18.B 19.B 20.D 21.B 22.D 23.A 24.B 提示：当a＞0时，y=的图像过一、二、三象限；当a＜0时，的图像过二、三、四象限。 25.D

26.C 27.D 28.D 提示：因为l过原点，所以C=0。又l过二、四象限，所以l的斜率—

二、填空题

三、解答题

38.提示：若a=b=0，则直线l过点（0，0）与（—2，2），可得直线l的斜率k=—l，此时直线l的方程为y=—x，即x+y=0。

综上可得，直线l的方程为x+y=0或x—y+4=0。

39.提示：（l）过点P 的直线l与原点的距离为2，而点P 的坐标为（2，—l），显然，过P（2，—l）且垂直于x轴的直线满足条件，此时l的斜率不存在，其方程为x=2。

若斜率存在，设l的方程为y+l=k（x—2），即kx—y—2k—l=0。

综上可得，直线l的方程为x=2或3x—4y—l0=0。

（2）过点P与原点O的距离最大的直线是过点P且与PO垂直的直线，如图l所示。

由l⊥OP，得kl·kOP=—l。因为所

图l

由直线方程的点斜式得y+l=2（x—2），即2x—y—5=0。故直线2x—y—5=0是过点P且与原点O的距离最大的直线，其最大距离为

（3）由（2）可知，过点P 不存在到原点的距离超过5的直线。

设与x+3y—5=0平行的一边所在的直线方程是x+3y+m=0（m≠—5），则点C到直线x+3y+m=0的距离d=解得m=—5（舍去）或m=7，所以与x+3y—5=0平行的边所在的直线方程是x+3y+7=0。

设与x+3y—5=0垂直的边所在的直线方程是3x—y+n=0，则点C到直线3x—y+n=0的距离d=得n=—3或n=9，所以与x+3y—5=0垂直的两边所在的直线方程分别是3x—y—3=0和3x—y+9=0。

故其他三边所在的直线方程为x+3y+7=0，3x—y—3=0和3x—y+9=0。

41.提示：（l）由已知可得l2的斜率存在，所以k2=l—a。

若k2=0，则l—a=0，a=l。

因为ll⊥l2，直线ll的斜率kl必不存在，所以b=0。

又因为ll过点（—3，—l），可得—3a+4=0，即a=（与a=l矛盾），可知此种情况不存在，所以k2≠0，即kl，k2都存在。

由k2=l—a，kl=，可得kkl2=—l，即①

由ll过点（—3，—l），可得—3a+b+4=0。 ②

由①②联立，解得a=2，b=2。

（2）因为直线l2的斜率存在，又ll∥l2，所以直线ll的斜率存在，可得kl=k2，即得③

又因为坐标原点到这两条直线的距离相等，且ll∥l2，所以ll，l2在y 轴上的截距互为相反数，即④

（2）因为A，B 的中点坐标为M（—2，3），直线x+y—2=0的斜率kl=—l，所以满足条件的直线方程为y—3=—（x+2），即x+y—l=0为所求的直线方程。

AB直的直线的斜率为k=—，所以满足条件的直线l的方程为y—2=—（x—l），即2x+3y—8=0。

所以直线BM 的斜率kBM=可得直线BM的方程为9x—5y+l3=0。

所以边AC的中线所在的直线方程为9x—5y+l3=0。

（2）设点D 的坐标为（x，y）。由已知可知M 为线段BD的中点，所以可得方程组

故点D（3，8）。

（3）由点B（—2，—l），C（2，3），得直线BC的方程为x—y+l=0。

所以点A到直线BC的距离为22。

45.提示：由已知条件可得圆M 的标准方程为（x—6）2+（y—7）2=25，所以圆心M（6，7），半径为5。

（l）由圆心 N 在直线x=6上，可设N（6，y0）。因为圆N 与x轴相切，与圆 M相外切，所以0＜y0＜7。圆N 的半径为y0，从而可得7—y0=5+y0，解得y0=l。因此，圆N 的标准方程为（x—6）2+（y—l）2=l。

设直线l的方程为y=2x+m，即2x—y+m=0，则圆心M到直线l的距离d

图l

故直线l的方程为2x—y+5=0或2x—y—l5=0。

46.提示：将圆C 的方程x2+y2—8y+l2=0配方得标准方程为x2+（y—4）2=4，则圆心坐标为（0，4），半径为2。

故所求直线l的方程为7x—y+l4=0或x—y+2=0。

47.提示：（l）圆C的方程化为标准方程为（x—3）2+（y—2）2=9，于是圆心C（3，2），半径r=3。

l—2。所以直线ll的方程为y—3=—2（x—5），即2x+y—l3=0。

（2）因为圆C的半径r=3，所以要使直线l2与圆C相交，则，可得|b于是可得b的取值范围是—32

（3）设直线l2被圆C截得的弦的中点为M（x0，y0），则直线l2与CM 垂直，于是可得，整理可得x0—y0—l=0。

因为点 M（x0，y0）在直线l2上，所以x0+y0+b=0。

（2）当直线 AB⊥x 轴时，x 轴 平 分∠ANB。

当直线AB的斜率存在时，设直线AB的方程为y=k（x—l），点 N（t，0），A（xl，yl），B（x2，y2）。

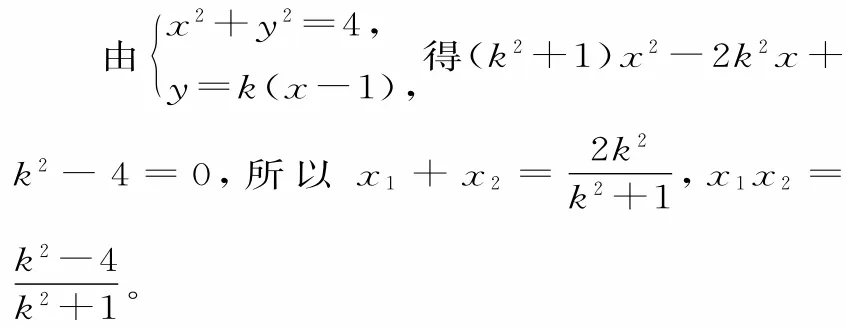
故当点N 为（4，0）时，能使得∠ANM=∠BNM成立，即x轴平分∠ANB。

49.提示：因为圆C和直线x—6y—l0=0相切于点（4，—l），所以过点（4，—l）的直径所在直线的斜率为其方程为y+l=—6（x—4），即y=—6x+23。

圆心在以（4，—l），（9，6）两点为端点的线段的中垂线上，即5x+7y—50=0上。由解得圆心坐标为（3，5），所以圆的半径为故所求圆的方程为（x—3）2+（y—5）2=37。

50.提示：l2平行于x轴，ll与l3互相垂直，画出简图，如图2所示。

三个交点A，B，C 连线构成直角三角形，经过A，B，C 三点的圆就是以AB为直径的圆。

图2

51.提示：以直线BC为x轴，线段BC的中点为原点，建立直角坐标系，如图3所示，则B（—l，0），C（l，0）。

设点A的坐标为（x，y）。

图3

当m2=l，即m=l时，对①式化简可得方程x=0，所以点A的轨迹是y轴。

当m2≠l时，对①式配方可得所以点A的轨迹是以为半径的圆（除去圆与BC的交点）。

52.提示：由题意可知点P 在圆上，即（—2—3）2+（l+l）2=r2，可得r=

53.提示：（l）设圆心P（x，y），圆P 的半径为r。由题设可得y2+2=r2，x2+3=r2，于是可得y2+2=x2+3。

故圆心P的轨迹方程为y2—x2=l。

（2）设P（x0，y0），由已知得又点P在曲线y2—x2=l上，从而可得

（责任编辑 郭正华）