“意外”收获“n2·2n”数列的求和公式

●蒋亚军 (宁波市第四中学,浙江 宁波 315016) ●苏茂鸣 (李惠利中学,浙江 宁波 315016)

“意外”收获“n2·2n”数列的求和公式

●蒋亚军 (宁波市第四中学,浙江 宁波 315016)
●苏茂鸣 (李惠利中学,浙江 宁波 315016)

按部就班的课堂教学是教师授课的主流，学生的“好问”“善问”常会带来课堂的“意外”收获.在介绍“等差乘等比”数列求和的例题后，有学生“意外”提出通项为an=n2·2n的数列能否用类似方法求和.抓住这个契机，师生一起通过观察特点、类比方法、分组化归等方法进行探究活动，不但“意外”收获该数列的求和公式，还对它进行了加强以及一般化的推广，最后通过裂项相消法、导数法、组合数公式以及阿贝尔变换数列求和公式等4种不同的方法对结论进行验证.

“n2·2n”数列；数列求和；裂项相消

学生的大胆提问是一种难得的教学资源，它往往能把平淡无奇的课堂变得精彩纷呈.笔者在上高一“数列求和”这节课时遭遇了“意外”，讲解错位相减法的例题后，有学生“意外”提出通项为an=n2·2n的数列能否用错位相减法求和.笔者决定放弃课前预设的教学计划，引导学生一起探究，“意外”收获该数列的求和公式.通过对它不断加强以及一般化推广的过程中，学生热情主动参与，在发现特点、类比方法、化归转化中体验数学学习的快乐.教师通过学习和研究，运用裂项相消法、导数法、组合数公式以及阿贝尔变换数列求和公式等4种不同的方法对结论加以验证和推广.课堂教学片段呈现如下：

1 例题呈现

题目 已知数列an=n·2n，求数列{an}的前n项和Sn.

解 由题意知Sn=1×21+2×22+…+n×2n，2Sn=1×22+2×23+…+n×2n+1，两式错位相减，得

-Sn=1×21+1×(22+23+…+2n)-n×2n+1，

从而

Sn=(n-1)2n+1+2.

生1：老师，若an=n2·2n，还能用错位相减法来求数列{an}的前n项和Sn吗？

2 探究互动

2.1 探究1

师：好，同学们，接下来我们一起来研究生1提出的这个问题.错位相减法的步骤是：乘公比，相减，除系数.由题意知Sn=12×21+22×22+…+n2×2n,我们先给Sn乘上公比,得

2Sn=12×22+22×23+…+n2×2n+1,

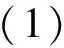
接下来该怎么办，新得到的式子有什么特点?

生2：得到的-Sn又是等差乘等比的形式，再进行一次错位相减，得

式(1)-式(2)，得

Sn=2+2×(22+23+…+2n)-(2n-1)×2n+1-n2×2n+1+n2×2n+2,

化简得

Sn=(n2-2n+3)×2n+1-6.

师：很好，生2观察仔细，发现了式(1)的特点，然后利用我们所熟悉的错位相减法再一次进行计算.既然我们使用了两次错位相减法解决这个问题，不妨把这种方法叫做“双错位相减法”.

(学生欣然接受.)

生3：老师，若an=n3·2n，怎么求Sn呢？

2.2 探究2

师：一起来试试.由Sn=13×21+23×22+…+n3×2n，2Sn=13×22+23×23+…+n3×2n+1，得

-Sn=(13-03)×21+(23-13)×22+…+[n3-(n-1)3]×2n-n3×2n+1,

即

接下来如何求解？

师：非常漂亮！通过尝试列出式子，观察通项[n3-(n-1)3]×2n的特点，利用分组求和的思想，转化成我们熟悉的(已掌握的)知识来解决问题，这体现了同学们转化问题、解决问题的能力.

生4：我算出最后的结果是Sn=(n3-3n2+9n-13)·2n+1+26.

2.3 探究3

师：很好，能不能加强到an=n4·2n？

生5：我算出来啦！乘上公比相减可得通项[n4-(n-1)4]×2n，拆开得(4n3-6n2+4n-1)×2n，接下来与上述方法类似，利用分组求和的方法，代入探究1和探究2的结论，最后得到结果是

Sn=(n4-4n3+18n2-52n+75)·2n+1-150.

师(追问)：很好，活学活用.利用分组求和的方法，结合前面探究的结论，采用整体代入的思想得出结论.若an=n5·2n呢，能否用刚才的方法解决？

生5：不好算了.探究1错位相减后是平方差公式，探究2错位相减后是立方差公式，探究3错位相减后可以看成是平方差，这些公式我们学过了，因此能解决.而5次方相减公式没学过，感觉算不出来.

师：总结得很好！这几个探究都有一个共同的特点，就是相减后都能利用基本公式化简成一个多项式乘2n的形式.既然次数高了不好解，我们能不能对多项式中的等差数列进行一般性地推广呢?

2.4 探究4

师：已知an=(an+b)2×2n，求数列{an}的前n项和Sn.

师：得出结论的同学，请分享一下你的思路.

生6：观察通项an=(an+b)2×2n=(a2n2+2abn+b2)×2n，分成(a2n2)×2n和(2abn+b2)×2n两组，第一组代入探究1的结论，第二组用一次错位相减法，最后两部分相加就可以了.只是具体答案还没有算出来.

师：思路清楚，计算仔细就能得到结论.这节课我们学习了错位相减法，一起探究得到了an=n2·2n的前n项和Sn=(n2-2n+3)2n+1-6，并以它为基础利用分组求和的思想探究了an=n3·2n，an=n4·2n的前n项和，最后对多项式中的等差数列进行一般化推广.由于时间关系，请同学们课后完成探究4.

看到学生们意犹未尽的样子，笔者认为这节课的探究值了.虽然没能完成既定的教学任务，但是真正做到了以学生为主体，尊重学生并且平等对待，让学生真正成为课堂的主人，积极主动地参与到数学课的研究中来，通过研究体验成功的快感，以此提高对数学的学习兴趣.

3 思维拓展

1)探究4的结论为Sn=a2[(n2-2n+3)2n+1-6]+2ab[(n-1)2n+1+2]+b2(2n+1-2).

2)虽然在课堂上用“双错位相减法”解决了an=n2·2n的前n项求和公式，对于它的求和公式的推导还有其他的方法.

方法1 (裂项求和)由n2·2n=[a(n+1)2+b(n+1)+c]·2n+1-(an2+bn+c)·2n，得a=1，b=-4，c=6，从而

n2·2n=[(n+1)2-4(n+1)+6]·2n+1-(n2-4n+6)·2n,

于是

Sn=[(n+1)2-4(n+1)+6]2n+1-(1-4+6)21=(n2-2n+3)2n+1-6.

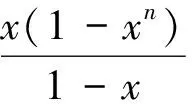
(3)

(4)

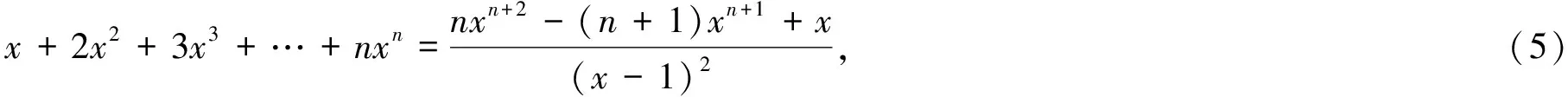
式(5)的两边再次求导得

式(6)两边同乘x得

(7)

在式(7)中令x=2，得

Sn=12×21+22×22+…+n2×2n=(n2-2n+3)2n+1-6.

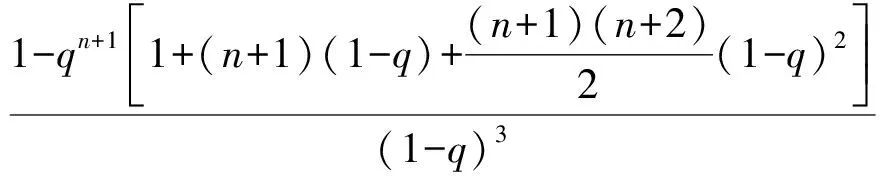
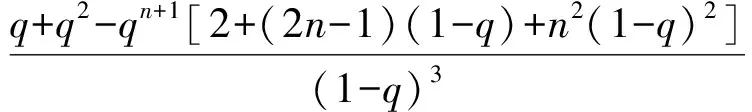
令q=2,得

Sn=(n2-2n+3)2n+1-6.

引理1[1]设{an}是二阶等差数列，{bn}是公比不为1的等比数列，则

(n-2).

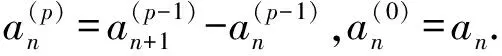
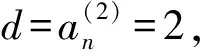
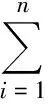
评注 裂项相消法是数列求和的基本方法，在很多高考题中都有所体现.导数法从函数的视角入手，既可以通过对x不断求导实现等差数列次数的增加，又可以通过对x的赋值实现对等比数列公比的推广；组合数公式也能实现对等比数列公比的一般性推广；阿贝尔变换数列求和公式的结论更具普遍性，适用范围更广.

4 反思

按部就班的课堂教学当然是教师授课的主流，但“意外”的课应当多一些较好[2].通过这次“意外”的探究课:首先，促进了学生学习方式的改变，从以往的“教师讲，学生听”到主动参与到对新知识和方法的构建，培养了学生的探索精神，增强了学生发现问题、转化问题和解决问题的能力，提高了学生的数学思维能力；其次，提高了教师驾驭课堂的能力，教师以一个协作者、促进者和指导者的角色参与其中，关注学生已有的知识基础和已具备的能力，将学生的探究活动设置在学生的“最近发展区”，让学生说思路、讲道理，注重学生对探究过程的经历[3]，学生的主体意识得到充分的体现；最后，促进了教师专业水平的发展，对探究结果意犹未尽，通过学习和尝试，从裂项相消法、导数法、利用组合公式以及阿贝尔变换数列求和公式等4种方法对结论进行验证和推广，开阔教学视野，实现教学相长.

[1] 裴东林.阿贝尔变换与数列求和[J].兰州文理学院学报:自然科学版, 2001, 15(4)：57-59.

[2] 苏克义.“意外”的一堂高三数学复习课——放飞思维[J].中学数学杂志,2017(1)：18-20.

[3] 蔡欣.一次没有预约的“美丽”[J].中学数学教学参考,2017(1/2)：20-22.

2017-05-16

蒋亚军(1982-)，男，台州仙居人，中学一级教师.研究方向：数学教育.

O122

A

1003-6407(2017)09-16-03