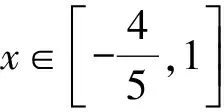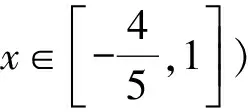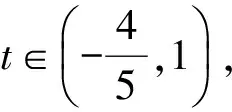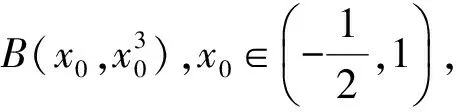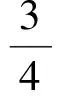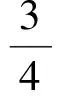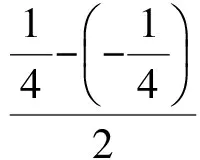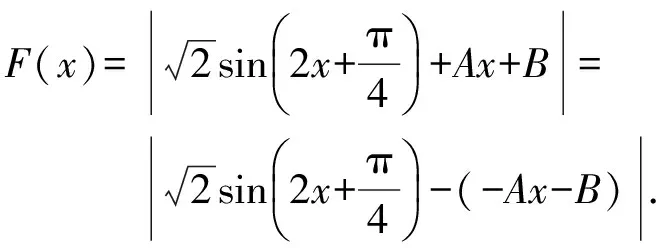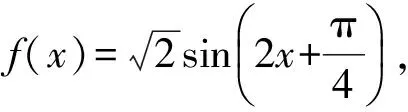形如|g(x)-ax-b|的函数最值问题破解之法
●陈素凤 (温岭中学,浙江 温岭 317500)
形如|g(x)-ax-b|的函数最值问题破解之法
●陈素凤
(温岭中学,浙江 温岭 317500)
形如|g(x)-ax-b|的函数最值问题,常是学生的拦路虎.文章通过回归基础、类比推广、猜想论证、变式拓展等研究得到此类问题的解决方法.
含绝对值函数最值问题;两直线夹逼;破解之法
形如|g(x)-ax-b|的函数最值问题,在近几年高中数学竞赛、自主招生、高考与学考中频繁出现,但由于涉及思想方法多、综合性强、分析能力要求高,许多学生只能望题兴叹.那么有无破解此类含参数绝对值最值问题的方法呢?笔者进行了一番探究,发现可借助两平行线夹逼性质来求解.
1 回顾基础,寻找突破
问题是思维的开端,是学习的起点,也是深入探索、研究的原动力.为解决上述问题,我们先从基础入手,寻找解决问题的突破口.
问题1 函数f(x)=|x-b|在区间[0,2]上的最大值为M(b),求M(b)的最小值.
解 因为-b≤x-b≤2-b,所以
M(b)=max{|-b|,|b-2|},
从而
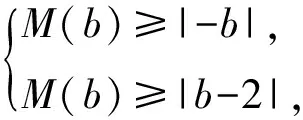
M(b)≥1,
当b=1时取到等号,即M(b)的最小值为1.
反思 根据函数y=x,x∈[0,2]的图像与函数y=b的图像关系发现:函数y=x,x∈[0,2]的图像夹在y=0与y=2之间,得
2 类比推广,初露端倪
在解题过程中,好的方法让人拍手叫绝,而优化解题就必然要进行类比、联想与转化.对于非直线型函数g(x),可以类比直线型函数的方法加以解决.
类比1 将x推广为任意函数g(x)
已知f(x)=|g(x)-b|,g(x)是闭区间上的连续函数,记g(x)最大值为g(x)max、最小值为g(x)min,若f(x)的最大值为M(b),求M(b)的最小值.
解 因为g(x)min-b≤g(x)-b≤g(x)max-b,所以
M(b)=max{|g(x)min-b|,|g(x)max-b|},
从而
于是2M(b)≥ |g(x)min-b|+|g(x)max-b|≥
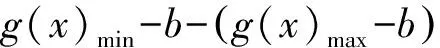
g(x)max-g(x)min,
即
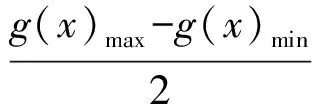
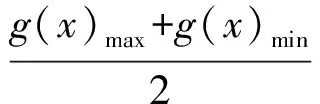
分析 推广研究发现:最值只与函数g(x)的最大值与最小值有关,因为g(x)的图像夹在y=g(x)max与y=g(x)min之间,所以
类比2 将直线y=b推广为y=ax+b
已知f(x)=|g(x)-ax-b|,g(x)是闭区间上的连续函数,记f(x)的最大值为M(b),求M(b)的最小值.
分析 因为g(x)-ax是闭区间上的连续函数,所以必存在最值.可以利用类比1求解此题,但是函数g(x)-ax含有参数a,给g(x)-ax最值的求解带来很大的难度,那么有没有其他解决方法呢?因为g(x)-ax-b是闭区间上的连续函数,所以g(x)-ax-b有最大值与最小值,不妨分别记为m,n,则
n≤g(x)-ax-b≤m,
从而
ax+b+n≤g(x)≤ax+b+m,
故g(x)的图像夹在y=ax+b+n与y=ax+b+m之间.下面可利用y=ax+b+n与y=ax+b+m的关系解决|g(x)-ax-b|的最值问题.
3 大胆猜想,合理论证
牛顿说过:没有大胆的猜想,就做不出伟大的发现.面对上述探索与思考,可得如下定理1:
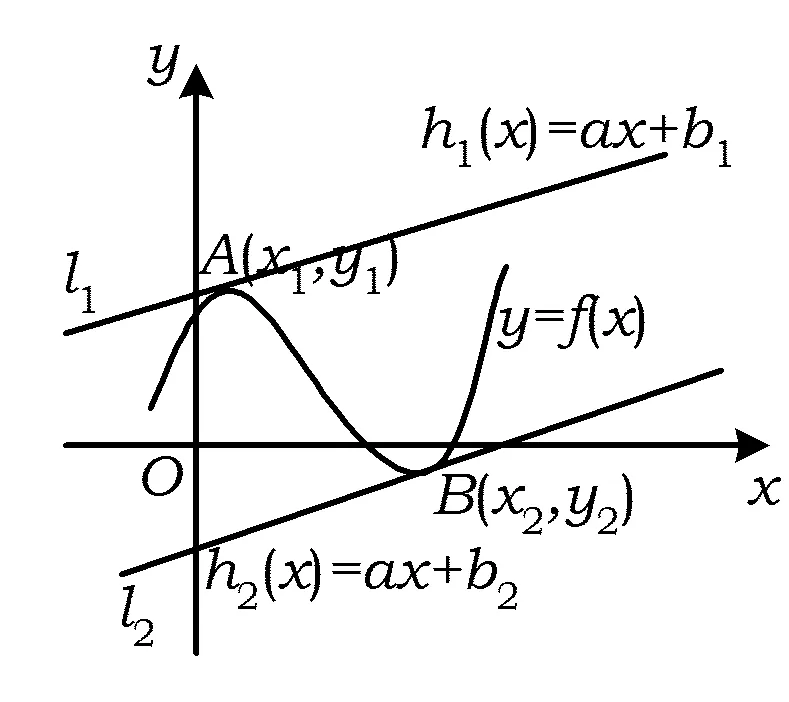
图1
定理1 已知y=f(x)是闭区间D上的连续函数.若存在函数h1(x)=ax+b1,h2(x)=ax+b2使得h2(x)≤f(x)≤h1(x)恒成立.设A(x1,y1)是h1(x)与函数y=f(x)的公共点,B(x2,y2)是h2(x)与函数y=f(x)的公共点,则当x=x1时,h1(x1)=f(x1)=y1;当x=x2时,h2(x2)=f(x2)=y2(如图1).记|f(x)-ax-b|在区间D上的最大值为M(b),则
证明 因为M(b)是|f(x)-ax-b|的最大值,所以
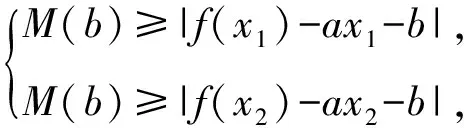
于是
事实上,类比1就是类比2当a=0时的特殊情况.

4 牛刀小试,豁然开朗
如果对定理1与类比1切实掌握,那么解决形如|g(x)-ax-b|的函数最值问题便小菜一碟.
( )
C.(-∞,1] D.(-∞,2]
(2016年4月浙江省数学学考试题第18题)
分析 由题意,可记M(b)为f(x)在x∈[1,2]上的最大值,则M(b)≥m对任意b恒成立.

图2
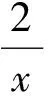
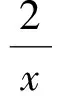
恒成立,从而

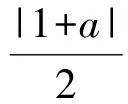
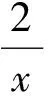
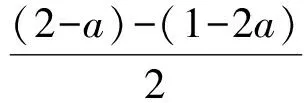
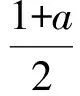
5 疑云再生,再次突破
我们已用定理1及类比1轻松地解决了例1,但不能就此罢休,笔者通过对例1题设条件的挖掘,得到如下变式:
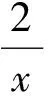
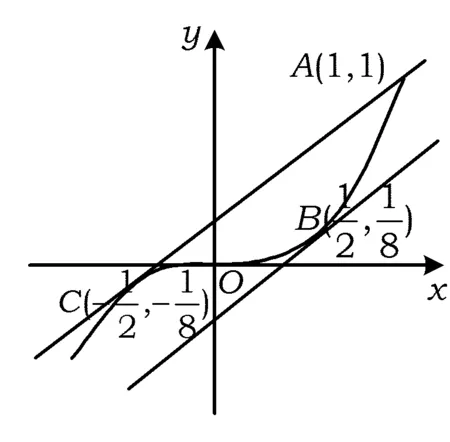
定理2 已知函数y=f(x),x∈D,函数图像上存在3个点A(x1,y1),B(x2,y2),C(x3,y3),满足x1 图3 证明 记g(x)=f(x)-ax-b,则 g(x1)=f(x1)-ax1-b, g(x2)=f(x2)-ax2-b, g(x3)=f(x3)-ax3-b, 又b1-b2=y1-kx1-y2+kx2= y1-y2-k(x1-x2)= 因为(x2-x3)(f(x2)-f(x1))-(x2-x1)(f(x2)-f(x3))=(x2-x3)(g(x2)-g(x1))-(x2-x1)(g(x2)-g(x3))=(x3-x2)g(x1)-(x3-x1)g(x2)-(x2-x1)g(x3),及|(x3-x2)g(x1)-(x3-x1)g(x2)-(x2-x1)g(x3)|≤ |(x3-x2)g(x1)|+|(x3-x1)g(x2)|+|(x2-x1)g(x3)|≤ 2(x3-x1)M(a,b), 所以2(x3-x1)M(a,b)≥|(x3-x2)g(x1)-(x3-x1)g(x2)-(x2-x1)g(x3)|=|(x2-x3)(f(x2)-f(x1))-(x2-x1)(f(x2)-f(x3))|=|(x2-x3)(y2-y1)-(x2-x1)(y2-y3)|= |x3y1+x2y3+x1y2-x1y3-x2y1-x3y2|= |(b1-b2)(x3-x1)|, 即 进一步便得到上述变式1的解答. 图4 y=-x+3. 易得 通过试题的变式与挖掘,可以将g(x)推广到二次、三次或更一般的形式,使问题进一步深化,从而扩大学生的认知范围. 图5 h1(x)≥f(x)≥h2(x) y=3t2(x-t)+t3. 因为切线过点A(1,1),所以 1=3t2(1-t)+t3, 化简得 (t-1)(2t2-t-1)=0, 易得 于是 进而 当f(x)不是多项式时定理2也成立,如1983年全国高中数学联赛二试第5题. 图6 在数学学习过程中,无论教师还是学生都会产生一些疑问,这些都是很好的生成资源.我们要学会抓住疑问,用数学的方法研究问题,逐步揭开难题神秘的面纱,掌握问题的本质,从而实现多题一解,让更多的师生脱离题海战术. 2017-05-27 陈素凤(1973-),女,浙江温岭人,中学一级教师.研究方向:数学教育. O122 A 1003-6407(2017)09-19-04
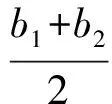

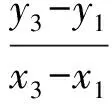
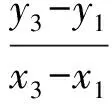
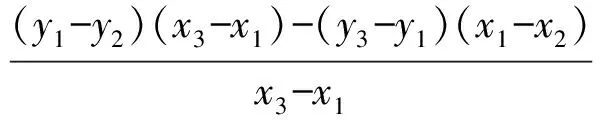
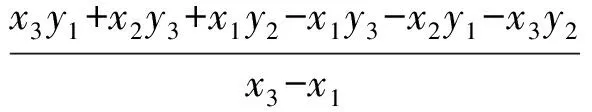


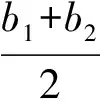

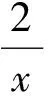

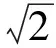
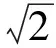

6 变式拓展,游刃有余