不忘初心 方得始终——基于2017年浙江省数学高考第21题

●金灿芳 (萧山中学,浙江 萧山 311200)

不忘初心 方得始终
——基于2017年浙江省数学高考第21题

●金灿芳
(萧山中学,浙江 萧山 311200)

解题中会有困惑与停顿，但解题中更有收获与快乐.文章从代数、几何、向量这3个方面探讨了2017年浙江省数学高考第21题的解法，多角度揭示了此题的本质，并由此提出了应对高考复习的教学建议.

代数；向量；解析几何

1 考题再现

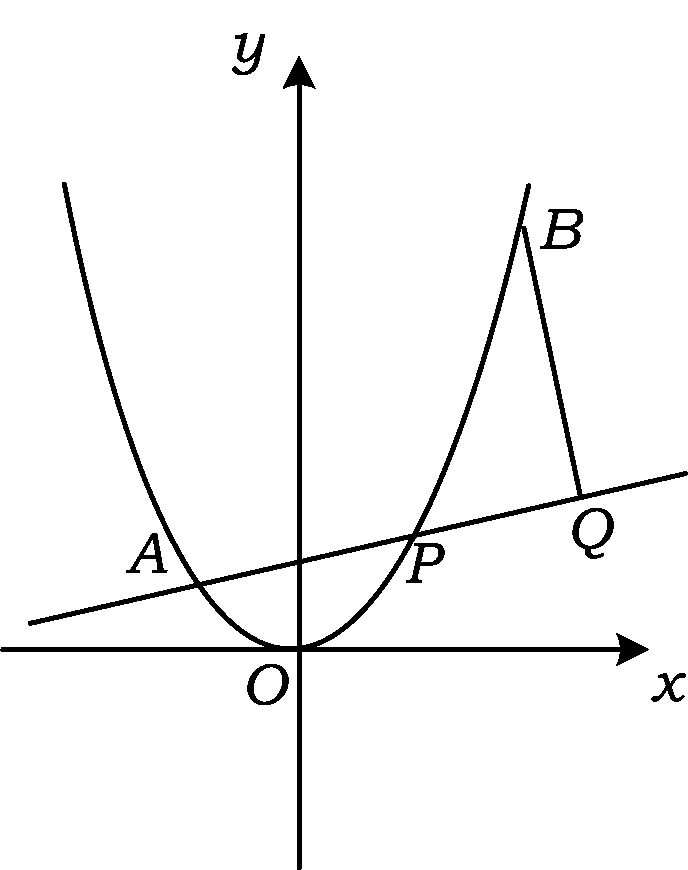
图1

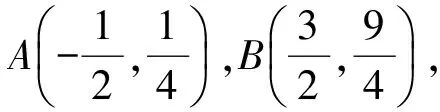
1)求直线AP斜率的取值范围；

2)求|PA|·|PQ|的最大值.

(2017年浙江省数学高考试题第21题)

此题作为文理合卷后首年的圆锥曲线大题，载体是抛物线与直线，兼具常规与新颖的特点.题目主要考查两点间的斜率公式、直线与圆锥曲线相交的弦长公式，题型中规中矩.本题可以通过代数、几何、向量等多种途径入手解答，不仅考查了学生的代数运算功底，也考查了学生从问题本质出发对问题的转化和化归能力，对学生有一定的挑战.

2 解法探究

视角1 代数的视角

1)解 设P(t,t2)，则

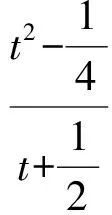
2)解法1 因为直线PA的方程为

(1)

而BQ⊥AQ,所以直线BQ的方程为

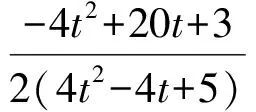
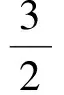
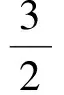
f′(t)=-4t3+3t+1=-(t-1)(2t+1)2,

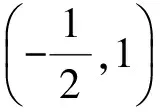
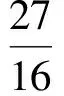
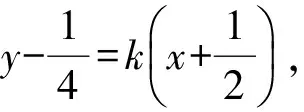
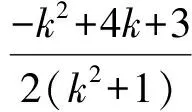
直线AQ与抛物线x2=y联立得

可得

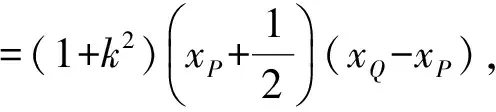
将xQ，xP代入，得

|PA|·|PQ|=(1+k3)(1-k).

令f(k)=(1+k)3(1-k)，则

f′(k)=(1+k)2(2-4k)，

从而

点评 第1)小题考查的是两点连线的斜率公式，直接设点的坐标代入，利用抛物线的标准方程进行消元即可.第2)小题的解决办法从代数的角度很直观，求出点Q的坐标，这也是大多数学生首先能想到的，但只有少部分学生按照这个思路能做到底，最主要的原因是运算遇阻.无论是解法1(设点P的坐标)还是解法2(设直线AQ的方程)都需要联立直线方程，求出点Q的坐标，这是代数方法的第一个难点.第二个难点是要用求导的方法求最值，解法2中f(k)的导函数较容易求得.在直线与圆锥曲线的位置关系中，代数法的繁琐不可避免，因此打下扎实的运算功底很重要，教师要注意培养学生优化运算的能力，比如本题能否避开求点Q的坐标.

视角2 几何的视角

1)解 因为y′=2x，则在点A处的切线方程的斜率为-1，而kAB=1,所以kAP∈(-1,1).

2)解法3 设P(t,t2)，由代数法知

则

直线BQ的方程为

从而点P到BQ的距离

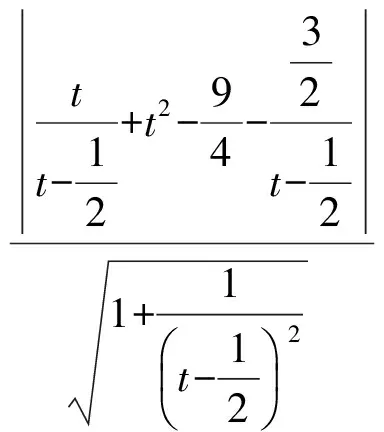
于是|AP|· |PQ|=d·|AP|=

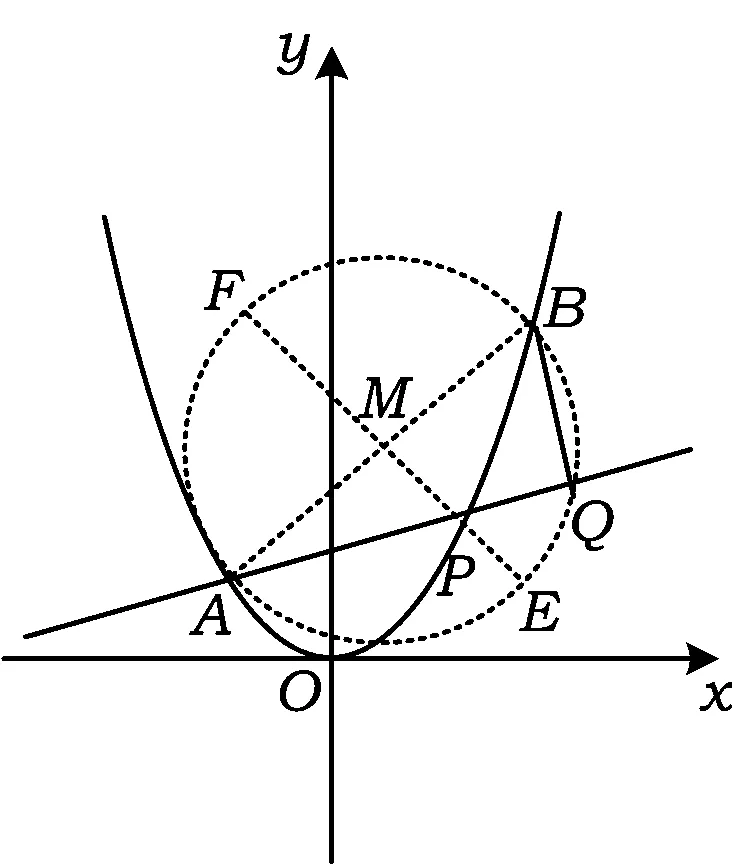
图2

以下同解法1.

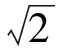
|AP|·|PQ|= |PE|·|PF|=

(R-|PM|)(R+|PM|)=

R2-PM2=2-PM2,

要求|AP|·|PQ|的最大值，即求PM2的最小值.设P(t,t2)，则

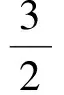
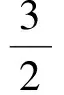
g′(t)=4t3-3t-1=(t-1)(2t+1)2,

从而

于是

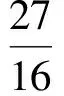
点评 解法3利用AQ⊥BQ这个条件，将|PQ|表示为点P到直线BQ的距离，避免了代数方法中最繁琐的点Q坐标的运算，当然还可以利用勾股定理来得到|PQ|，即转化为求点B到直线AQ的距离.解法4利用圆幂定理，因为点Q在以AB为直径的圆上，所以

|AP|·|PQ|=|EP|·|FP|，

即转化为求|PM|的最值；求|PM|2的最值采用两点间的距离公式来表达，不仅避免了求点Q的坐标，还避免了点到直线的距离公式.几何方法相对快速地获得了|AP|·|PQ|所对应的解析式，实现了运算上的优化，后面求导的部分与代数法一致.

视角3 向量的视角

向量的方法主要针对第2)小题.

解法5 设P(t,t2)，则

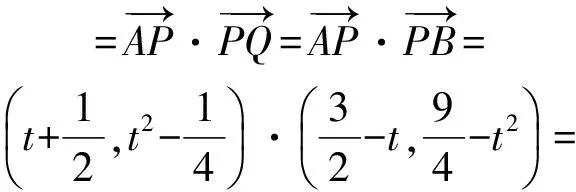
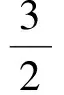
以下同解法1

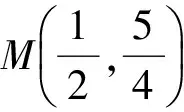
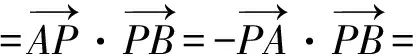
-(PM2-AM2)=-(PM2-2),

以下同解法4.

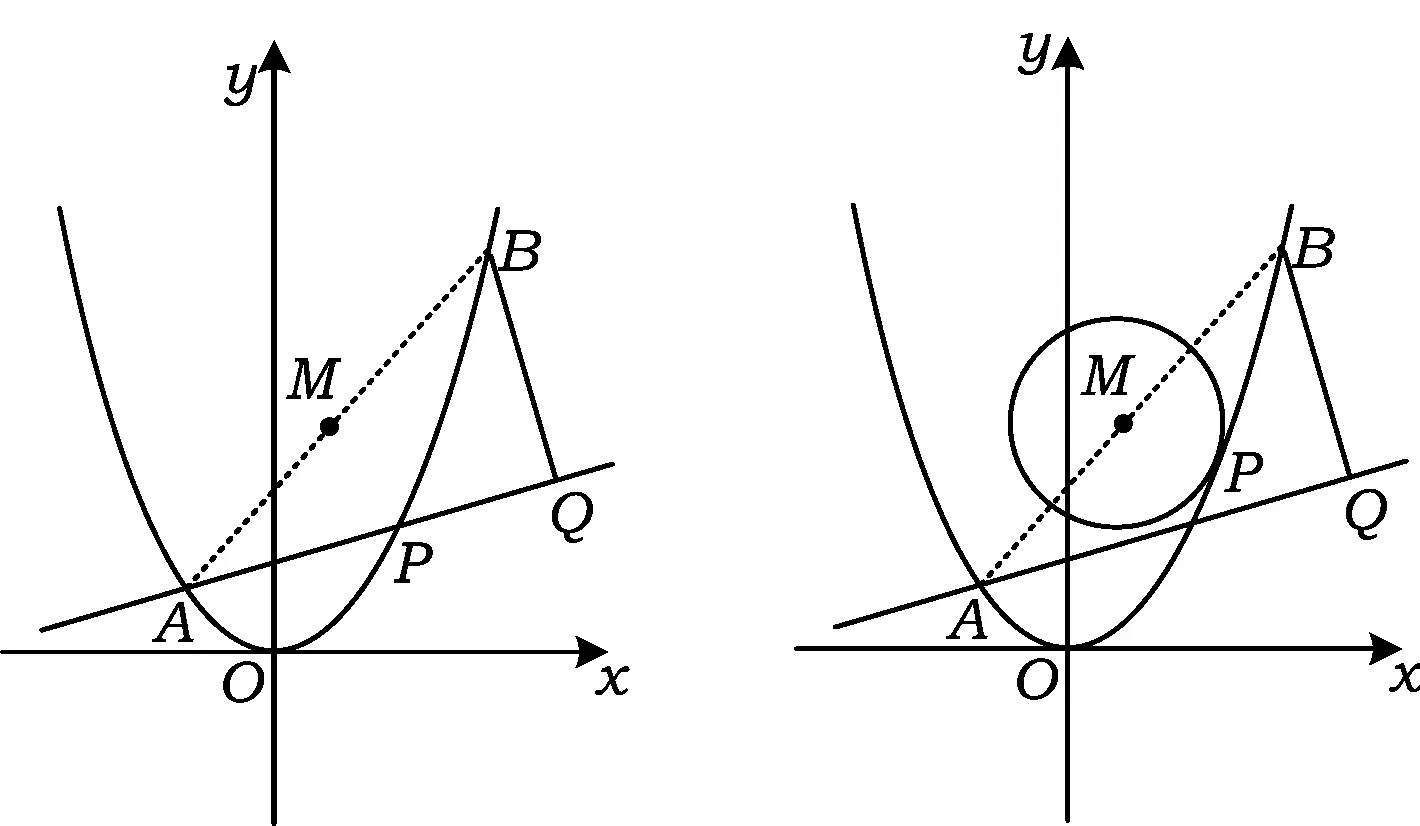
图3 图4

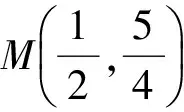
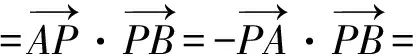
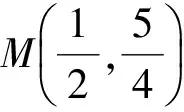
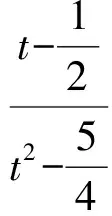
抛物线在点P处的切线斜率为k2=2t，从而

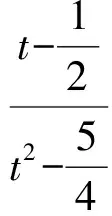
即

4t3-3t-1=0,

解得t=1，故

点评 向量法是本题的亮点，核心就是利用向量的几何意义得到

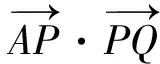
之后的处理又可以分成两种情况.解法5直接用向量的坐标表示来表达数量积，简洁明了地得到解析式.解法6和解法7用极化恒等式将最值转化为求|PM|的最值，|PM|的最值可以用两点间的距离(同视角2)，也可以用几何上的特殊情况来解决，因为|PM|取最小值时就是以M为圆心的圆与抛物线相切，所以解法7中利用圆与抛物线相切的公切线方程很快地得到了切点坐标.

3 解后反思

3.1 夯实基础，提升能力

对于圆锥曲线大题，有句老话：“圆锥曲线无难题”，但是也有一句很讽刺的话：“有些高中生到毕业了也没能完整地做完一道大题.”圆锥曲线的大题以常规题居多，无论是求最值还是证明定值，总少不了联立方程、韦达定理、弦长公式等常规手段.本题也不例外，可以用韦达定理表示点P的坐标，用弦长公式来表示|PA|·|PQ|，这样看来没有难点，但是这些常规步骤的运算量都不小.很多学生就败在运算上——联立、判别式等等都容易求错，只要有一个小地方求错，后面的化简就不成功了.还有一些学生运算遇阻时常猜测答案，甚至直接放弃，认为算算的东西总会的，这是学习上的“纸上谈兵”，一到真枪实战的考场，狐狸尾巴就露出来了.因此，教师要不断地提醒学生打磨自己的运算功底，越不顺利越要找到原因，每做一题都要争取做到底，找到自己算不对的地方，吸取失败的教训，积累经验，只有这样才能提高自己的运算能力.

3.2 重视概念，关注本质

概念是最容易被学生忽视的，因为学生认为它没什么内容，太简单了.其实很多题目归根究底就是在考概念和定义.比如向量数量积的定义，考生几乎都知道向量数量积的几何意义，大部分学生也能答上来，并且教科书上讲投影这块内容的图和本题的图非常相似，但是在考试中，只有很少的学生能把结果转化为数量积，归根结底还是对概念的本质没有研究透，挖得不够深.教师首先要重视概念，重视概念本质的挖掘，在平时的讲解中要渗透，还要引导学生梳理概念，再结合已经做过的题打磨概念，做到“以不变应万变”[1-2].

3.3 研究专题，优化解题

英语中的单词是有词根的，一个词根能关联一连串的单词，数学也是一样，我们会有一些母题，也可以称之为题根.那么在高考复习时，教师按专题整理或引导学生整理就尤为重要.不仅如此，我们还可以把题根做多角度的延伸，或通过某条思路串起看似不同专题的题，这在某种程度上也可以培养学生转化与划归的能力.具备这样的能力，在不经意间就优化了解题过程.众所周知，运算是圆锥曲线问题的一个难点，可以把优化运算作为一条线索来整理，比如消哪个元，计算三角形或四边形的面积时要找到最简单的表示方法，计算距离时要尝试一下弦长公式，处理定点问题时可以先设点再证明，能不能用几何或向量思路来转化等等[3].

2017年的高考已经结束，有些高考题平淡中透着惊喜，就看学生们能否正确把握，用心地打磨运算功底，用心地挖掘概念本质，用心地研究专题分类，正所谓“不忘初心，方得始终”.

[1] 李学军，曲文瑞.大音希声 大象无形——基于2016年浙江省数学高考理科第15题[J].中学教研(数学),2016(12):43-46.

[2] 曹凤山.数学教学 把根留住——2015年浙江省数学高考试题解读[J].中学教研(数学)，2015(8)：1-4.

[3] 高考数学研究组.浙江高考数学2004一路走来[M].杭州：浙江大学出版社，2016.

2017-07-20

金灿芳(1982-),女,浙江萧山人,中学一级教师.研究方向:数学教育.

O123.1

A

1003-6407(2017)09-38-04