2017年全国卷Ⅱ文科第21题评析
●戚有建 (扬州中学,江苏 扬州 225009)
2017年全国卷Ⅱ文科第21题评析
●戚有建
(扬州中学,江苏 扬州 225009)
文章研究2017年全国数学高考新课标卷Ⅱ文科第21题的多种解法及深刻背景.
泰勒公式;ex≥x+1;压轴题
1 考题展示
例1 已知函数f(x)=(1-x2)ex,
1)讨论f(x)的单调性;
2)当x≥0时,f(x)≤ax+1,求a的取值范围.
(2017年全国数学高考新课标卷Ⅱ文科试题第21题)
分析 本题是2017年该卷的压轴题,考查的是导数的应用.第1)小题重点考查用导数研究单调性,多数学生都能解决;第2)小题重点考查用导数研究不等式恒成立问题,同时考查分类讨论、转化化归的数学思想,该小题入口较宽,解法多样,背景丰富,有一定难度和区分度,也有很大的教学价值和研究空间[1].
2 解法研究
1)解f′(x)=(1-2x-x2)ex,令f′(x)=0,则
x2+2x-1=0,
即
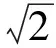
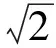
下面重点研究第2)小题.
2)解 由题意可知:对任意x∈[0,+∞),不等式(1-x2)ex≤ax+1恒成立.
方法1 构造差函数,研究g(x)=(1-x2)ex-ax-1的最值.
令g(x)=(1-x2)ex-ax-1,x∈[0,+∞),则
g′(x)=(1-2x-x2)ex-a,
从而
g″(x)=-(x2+4x+1)ex<0,
于是g′(x)在[0,+∞)上单调递减.又g′(0)=1-a,因此
①当a≥1时,g′(x)≤g′(0)=0,从而g(x)在[0,+∞)上单调递减,于是g(x)≤g(0)=0,符合要求.
②当0≤a<1时,
g′(0)=1-a>0,g′(1)=-2e-a<0,
又g′(x)在[0,+∞)上单调递减且连续,由零点存在性定理得∃x0∈(0,1),使得g′(x0)=0.且当x∈(0,x0)时,g′(x)>0,从而g(x)在[0,+∞)上单调递增,于是g(x)>g(0)=0,不符合要求.
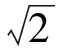
综上所述,a的取值范围是[1,+∞).
点评 方法1是处理含参不等式恒成立问题常用的方法,也就是将不等式恒成立问题转化为差函数最值问题,然后研究不等式“g(x)max≤0”,该方法通俗易懂,学生容易想到.但由于本小题中引入了参数a,因此需要对参数a分情况讨论处理,这对学生的思维能力提出了较高要求,另外在0≤a<1的情形中还会遇到“g′(x)=(1-2x-x2)ex-a,x∈[0,+∞)的零点不方便求出”的困难,这里需要通过“设而不求”来处理,这对学生来说有一定难度.

①当x=0时,不等式(1-x2)ex≤ax+1恒成立,从而a∈R.
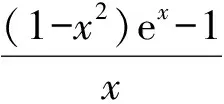

又令h(x)=(-x3-x2+x+1)ex+1,x∈(0,+∞),则
h′(x)=-x(x2+4x+1)ex<0,
从而h(x)在(0,+∞)上单调递减,于是
h(x) 即 g′(x)<0, 亦即g(x)在(0,+∞)上单调递减,因此 综上所述,a的取值范围是[1,+∞). 方法3 借助不等式(1-x)ex≤1放缩处理. 先证(1-x)ex≤1,x∈R.设d(x)=(1-x)ex-1,则 d′(x)=-xex. 令d′(x)=0,则x=0:当x∈(-∞,0)时,d′(x)>0,从而d(x)在(0,+∞)上单调递增;当x∈(0,+∞)时,d′(x)<0,从而d(x)在(-∞,0)上单调递减,于是 d(x)max=d(0)=0, 进而 d(x)≤d(0), 即 (1-x)ex≤1, 当且仅当x=0时,等号成立. 借助(1-x)ex≤1可得:当x≥0时, f(x)=(1-x2)ex=(1-x)(1+x)ex≤x+1, 又当x≥0时,f(x)≤ax+1,故a的取值范围是[1,+∞). 点评 方法3实际上是借助不等式(1-x)ex≤1来处理,简洁漂亮,简直是“秒杀”,让人赏心悦目,大呼痛快、精彩.同时,也引起我们的思考:不等式(1-x)ex≤1是如何想到的呢,有何背景? 不等式(1-x)ex≤1看似平凡其实很不平凡,它实际上是不等式ex≥x+1的变形,用-x去换ex≥x+1中的x,得 e-x≥1-x, 两边同乘以ex即得 (1-x)ex≤1. 而不等式ex≥x+1更是大有来头,它来源于高等数学中的泰勒公式:f(x)=ex在x=0处的泰勒展开式为 即 故 ex≥x+1. 这样就不难理解本题的命制过程了,首先根据泰勒公式得到ex≥x+1,用-x去换ex≥x+1中的x,得e-1≥1-x,两边同乘以ex即得(1-x)ex≤1,两边再同乘以1+x(其中x≥0)即得 (1-x2)ex≤x+1, 然后隐掉x前面的系数1,改成求参数a的取值范围,这就是本题的命制过程. 例2 设函数f(x)=ex-1-x-ax2, 1)当a=0时,求f(x)的单调区间; 2)若当x≥0时都有f(x)≥0,求实数a的取值范围. (2010年全国数学高考新课标卷Ⅱ文科试题第21题) 分析 第2)小题的命制背景是泰勒公式 首先根据泰勒公式得到不等式 例3 设函数f(x)=x(ex-1)-ax2, 2)若当x≥0时都有f(x)≥0,求实数a的取值范围. (2010年全国数学高考新课标卷Ⅱ理科试题第21题) 分析 第2)小题中f(x)≥0,即 ex-1-ax≥0, 命题背景也是泰勒公式 首先得到不等式ex≥x+1,然后隐掉x前面的系数1,改成求参数a的取值范围. 例4 已知函数f(x)=axn(1-x)+b(其中x>0,n∈N*,a,b为常数),曲线y=f(x)在(1,f(1))处的切线方程为x+y=1. 1)求a,b的值; 2)求函数f(x)的最大值; (2012年湖北省数学高考文科试题第22题) 分析 第3)小题只要证 即 亦即 即 例5 已知函数f(x)=ex-ln(x+m), 1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性; 2)当m≤2时,证明:f(x)>0. (2013年全国数学高考新课标卷Ⅱ理科试题第21题) 分析 第2)小题中,当m≤2时, ln(x+m)≤ln(x+2), 即只要证ex>ln(x+2).实际上,由不等式lnx≤x-1可得 ln(x+2)≤x+1, 又因为ex≥x+1,并且上面两个不等式中的等号不能同时取到,所以ex>ln(x+2). 例6 设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数. 1)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求gn(x)的表达式; 2)若f(x)≥ag(x)恒成立,求实数a的取值范围; 3)设n∈N+,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明. (2014年陕西省数学高考理科试题第21题) 分析 第3)小题只要证 令b1+b2+…+bn=ln(n+1),则 即 例7 已知函数f(x)=lnx+a(1-x), 1)讨论f(x)的单调性; 2)当f(x)有最大值,且最大值大于2a-2时,求a的取值范围. (2015年全国数学高考新课标卷Ⅱ文科试题第21题) 分析 第2)小题的命制背景也是泰勒公式,首先得到不等式lnx≤x-1,左、右两边加2得到不等式lnx+2≤x+1,然后将在不等式的右边添参数a改为含参不等式lnx+2≤a(x+1),即 lnx+a(1-x)≤2a-2, 这就是本题的命制过程. [1] 姜卫东,戚有建.一道调研题引起的研究[J].中学教研(数学),2015(4):20-22. [2] 戚有建.2012年湖北卷文科压轴题分析[J].中学数学研究,2013(4):9-10. 2017-07-20 戚有建(1977-),男,江苏扬州人,中学高级教师.研究方向:数学教育. O122.1 A 1003-6407(2017)09-47-04
3 背景研究


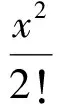
4 背景应用