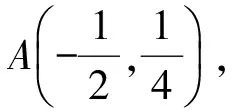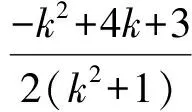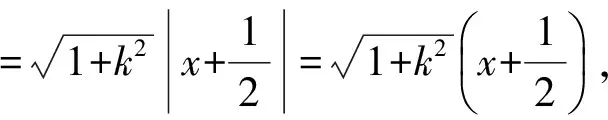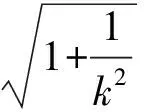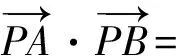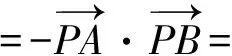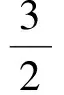扎根概念 挖掘本质 优化策略
——基于高考向量背景题的思考
●马喜君 丁晨芳 (元济高级中学,浙江 海盐 314300)
●赵琴学 (海盐高级中学,浙江 海盐 314300)
扎根概念 挖掘本质 优化策略
——基于高考向量背景题的思考
●马喜君 丁晨芳 (元济高级中学,浙江 海盐 314300)
●赵琴学 (海盐高级中学,浙江 海盐 314300)
数学学科能力与学科素养必然扎根于概念,由概念构建知识网络系统,进而深挖问题的数学本质,基于本质优化策略.文理合卷即统一知识点,统一要求,统一考核.教师应该调整自己原有的理念、行为方式,转换自己对于高考的理解,扎根概念挖掘本质,转换思考角度、高度、宽度,优化策略——提出问题的本质解法、发展优化解法,整合知识、方法与思想,从而提升数学核心素养.
概念;本质;优化策略
2017年是浙江新高考元年,数学试卷因文理合卷、内容调整而备受期待.文理合卷即统一知识点,统一要求,统一考核.所谓的文与理,是教师经历、理念、行为方式中的旧印记.因此文理合卷后不是学生应该如何处理,而是教师应该如何调整,转换自己对于高考的理念,转换思考角度、高度、宽度,寻找最有利、最高效的考前复习策略.
所有的数学学科能力与素养必然扎根于概念,由此内化为知识网络的节点,构建自己的结构化知识网络系统,进而深度挖掘问题的数学本质[1],基于本质优化策略——提出问题的本质解法、发展优化解法,整合知识、方法与思想,从而提升数学核心素养.笔者结合平时的教学与高考试题解答后的思考,在深化学生对核心概念的理解与掌握、提高学生的数学综合能力、形成数学核心素养方面等作了一些探究和思考.

图1
1 忠于概念理解,优先定性分析
数学学习基于概念,考核忠于概念,应用高于概念,学好数学的一个表征量就是能灵活地运用概念定性地分析问题的数理关系,然后才是定量计算.
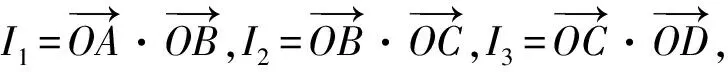
( )
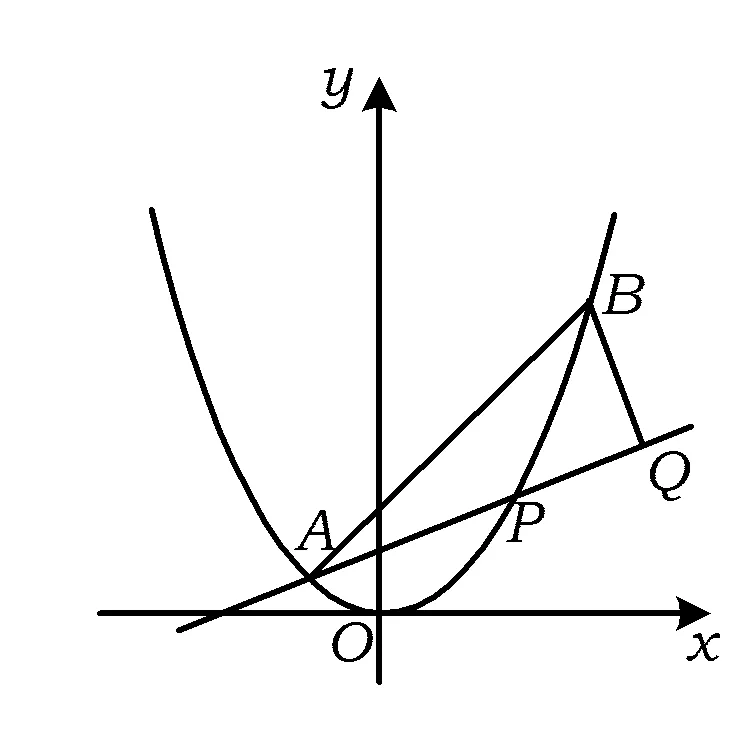
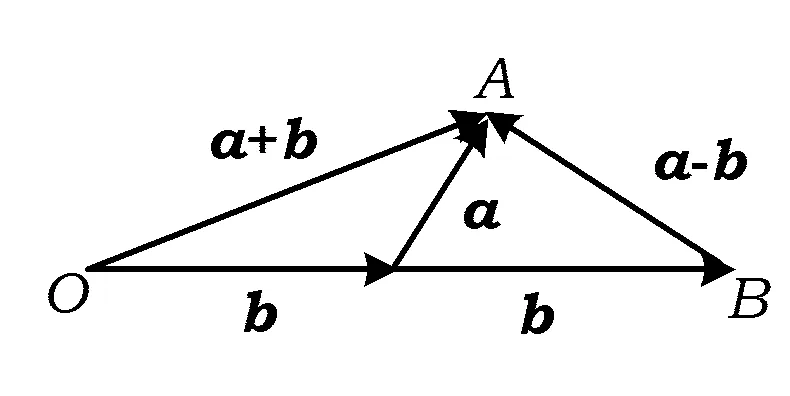
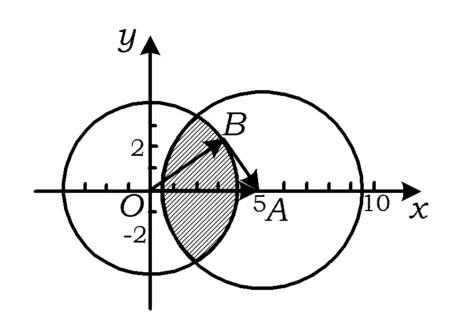
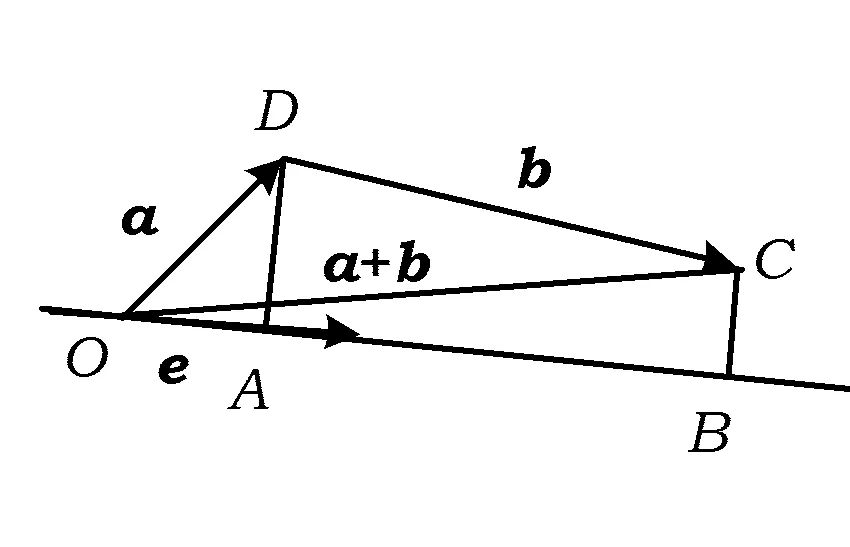
A.I1 C.I3 (2017年浙江省数学高考试题第10题) 视角1 向量数量积的概念是 a·b=|a|·|b|cos 根据题意判断可知: ① ∠AOB是钝角,∠BOC是锐角,从而 I1>I3, 故 I2>I1>I3. 视角2 可以用作差的方法处理比较大小的问题.由 得 I2>I1; 由 得 I2>I3; 得 I1>I3. 故 I2>I1>I3. 图2 核心概念在整个高中数学的学习中起到统领、主导的作用.学生抓住核心概念就等于抓住了高中学习的命脉;学生掌握核心概念就等于掌握了高中数学的根本.由此可见,学生解决问题的关键在于对概念的理解和掌握. 例2 如图2,已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是______,最大值是______. (2017年浙江省数学高考试题第15题) 试题简明扼要,浙江风格明显,考查学生处理向量的加减运算能力,同时涉及三角形法则、平行四边形法则,探究不同的运算方法. 解法1 如图2可得 |OA|+|AB|≥|OB|, 在△OAB中,两边之和大于第三边,当点A在线段OB上,即向量a,b共线时,上式取到等号,即|a+b|+|a-b|的最小值为|OB|=2|b|=4. 向量部分最核心的是向量的加、减运算及其几何意义,也就是三角形法则、平行四边形法则,以及向量的数量积定义及其几何意义.抓住这些核心,问题迎刃而解.概念、原理的理解不是文字的背诵,而是意义的解读,在具体问题情境下剖析问题中的概念本质,便得以窥见问题的构造背景. 平面向量数量积概念的两种表征体现了数量积“数”与“形”的双重身份.首先,向量数量积的概念定义是:a·b=|a|·|b|cos 思路1 应用定义解题.在已知向量中选定基底向量,将所求向量转化为基底向量进行代数求解. 4a·b=a·4b=a·[a-(a-4b)]= 图3 图4 数学概念是从现象、事实中抽象出来的理性知识,是数学问题构建的理论背景和基本材料.如何在学生已有的概念认识上解析问题中的概念,如何引导学生在环环相扣的变式设计中清晰地识别深层知识的核心思想、不断深化对核心概念的理解,借以发展学生超越客观问题的构想思维,促进其思想与感觉、观念与实体的统一,并有助于学生将学习结果内化,不断地将学习过程引向更深、更有意义的方向[2]. 例3 如图4,已知平面向量a,b,|a|=1,|b|=2,a·b=1,若e为单位向量,则|a·e|+|b·e|的最大值是______. (2016年浙江省数学高考文科试题第15题) 基于对向量数量积的概念认识,分析如下: 从而 即 这些结论对我们解决问题有何帮助呢?逆向剖析概念,|a·e|+|b·e|是向量a,b在e上的投影之和,结合图像不难发现 |a·e|+|b·e|= |OA|+|AB|=|OB|≤ 在Rt△OBC中,直角边总不大于斜边,当e与a+b共线时,上式取到等号. (2016年浙江省数学高考理科试题第15题) 在例2的分析基础上,可得类似的结论: |a·e|+|b·e|= |OA|+|AB|=|OB|≤ |OC|=|a+b|, 此类问题回归了一个本质问题:|a|,|b|,|a+b|这3个向量的模长的关系. 例4 同例2. 基于投影概念(解法1)解析后,向量的坐标形式也是经常应用的形式,尤其是对于模长恒定的向量,间接地整合了向量与三角函数的关系[3]. 解法2 向量a,b是两个动态向量,可以先固定一个,不妨设a=(1,0),b=(2cosθ,2sinθ),则 从而16≤t≤20,故 除了上述的解题策略外,对于一些结构较复杂的目标式,还可以采取整体代换的“旋转变换”,使得目标式简明扼要,关系明了. 解法3 设a+b=u,a-b=v,则 |u+v|=2, |u-v|=4, 从而 |u|+|v|≥max{|u+v|,|u-v|}=4, (|u|+|v|)2≤|u+v|2+|u-v|2=20, 因此 与前几年相比,2017年解析几何大题的考查角度变化较大,首先曲线载体选择了抛物线,更便于坐标运算,其次求解目标|PA|·|PQ|的最大值,结合图像发现具有强烈的向量背景. 图5 1)求直线AP斜率的取值范围; 2)求|PA|·|PQ|的最大值. (2017年浙江省数学高考试题第21题) 1)略. 2)解 联立直线AP与直线BQ的方程 该解法要求直线QP与BQ的直线方程,联立方程求出点Q,继而求出|PA|,|PQ|的长度,运用代数方法求最值.解题的过程采用传统解析几何的通性通法,中规中矩,计算繁琐,很多学生求出|PA|,|PQ|的长度后思维有点模糊,解法有点混乱.根据向量的几何意义, |PA|·(-|PQ|)=-|PA|·|PQ|, 上述解法清晰自然,避免了繁琐的运算,简化了解析几何的解答过程,提高了学生运算的正确率. 2017年的浙江省数学高考卷开启了文理合卷的新篇章,试卷关注学生,注重基础,凸显能力,对高中数学教学起到了很好的导向作用.对今后中学教学的启示:面对文理合卷,如何针对不同思维层次的学生因材施教;面对选考的冲击,如何科学合理地调整数学复习教学节奏、改进数学学习方式,值得我们进一步思考与探索. [1] 华志远.透视数学核心素养 漫话课堂转型抓手——从《函数与方程》的教学实录谈起[J].数学通讯,2016(7):27-30. [2] 卢明,姜巍.关注核心概念 培养核心素养[J].数学教学研究,2016(7):7-12. [3] 卢明.平面向量复习要强化“5种意识”的培养[J].中学教研(数学),2014(4):1-5. 2017-07-22 马喜君(1979-),男,浙江嘉兴人,中学高级教师.研究方向:数学教育. O123.1 A 1003-6407(2017)09-44-04
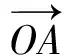
2 基于概念思考,明确思维导向
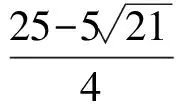
3 勇于挖掘本质,透视构题背景
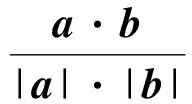
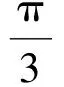
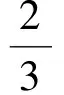
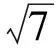
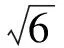
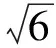
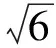
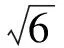
3 善于联系迁移,优化解题过程
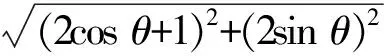
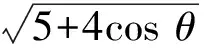
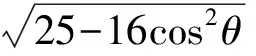
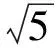
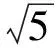
4 敢于交汇整合,简化解题过程