在数与形之间感受数学的生命

朱晴

摘 要：数与形，是数学中两个相互依存的体系。以形释数，以数载形，数形结合，成为数学教学的基本思想和方法。对于小学生而言，这种思想的渗透、方法的指导是循序渐进的、潜移默化的。要从初步的感知上升到理论高度，并形成一定的意识，最终养成良好的习惯，需要长时间的积累和大量的实践来完成。

关键词：数学；数与形；教学案例；数形结合

人教版第十一册《数与形》是近年新增的教学内容，严格地说来，它是一堂知识归纳课，更是一堂数学中的“思想品德”课。如何让这堂“思想品德”课达到最优境界？如何让学生在数与形的结合与转化中体会它们的关系？如何让枯燥的数字和图形变为生活神奇的数学魔方，使之说话舞蹈，成为一个鲜活的生命，增强它的生命力？笔者想借自己上的录像课《数与形》和大家分享一些体会。

片段一：找准“思想”原生点——设疑

师：（课件出现一个圆）这是一个圆，用数字1来表示，接着出现三个圆（宝塔形），用数字3来表示。请你猜一猜，接下来会出现什么样的图形？用数字几来表示？请同学们把答案记在心里，（老师出示结果为6个圆）你猜对了吗？那接下来又会出现什么样的图形？

生：10个。

师：（出示结果）真棒，猜对了。（如图1）

师：看来，数与形之间的确存在着某种联系和规律。今天这节课，我们就来研究数与形。

评析：《新课标》指出：学生的知识技能有“生长点”和“最近发展区”，学生的数学思想、数学情感同样具有较为清晰的“生长点”和“最近发展区”。学生们在低年级就学习了看图写数，看图写算式，中年级接触了看线段图列式，初步感知了用图形与字母符号来表示数，先“形”后“数”的思维占主导地位。高年级在解应用题、画统计图等学习实践中慢慢实现“先数后形”的转化，抽象思维开始得到培养。那么，学生思维的“最近发展区”在哪儿呢？通过钻研教材，课前谈话，笔者把“体会数与形的联系”“积累数形结合解决问题的活动经验”“培养学生数形结合的数学思想意识”作为本课的教学重点。那么，这一个片断的设计既有数、又有形，既有猜想、又有印证，找准了学生的思维入口，引起学生学习的兴趣，为后面的思维训练、方法训练做好了铺垫。

片段二：对准兴趣激发点——活动

师：老师这儿有一个正方形，用数字几表示？

生：用数字1表示。

师：如果老师再增加三个正方形，一共有几个正方形？怎样列式计算？

生：一共四个正方形，用1+3来计算。

师：它的和能拼成一个什么样的图形？

（学生分组进行拼一拼，摆一摆。有的拼成了一个长方形，有的拼成了一个正方形，还有的拼成一个宝塔形，还有个别的学生拼成了一个不规则图形）

师：如果再增加5个正方形，又能拼成一个什么图形呢？

（学生继续拼、摆，请部分学生把拼、摆的图形呈现在展台上）

师：比较、观察，这两组图形中，哪一种图形可以很清楚简便地计算出总数？

生：正方形。

师：为什么？

生：因為正方形的面积等于边长乘边长，只要数出一条边的长度，就可以很快地计算出面积。

师：（展示拼图：一个小正方形再加三个不同颜色的小正方形得到一个较大的正方形，可以用2乘2来计算，也可以用2的平方来表示；一个小正方形再加三个不同颜色的小正方形再加五个不同颜色的小正方形得到一个有着三种颜色的较大正方形，可以用3乘3来计算，也可以用3的平方来表示。分别展示在黑板上。）想象一下，1+3+5+7的和也可以是个什么图形？

生：正方形。

生：一个边长是4的正方形。

师：（把1+3+5+7的和所拼成的正方形展示出来，如图2）是这样吗？和可以用多少来表示？

生：1+3+5+7=4的平方。

师：观察三个算式和图形，你有什么发现？

生：有几个加数结果就等于几的平方。

生：有几个加数就可以拼成一个有几层的正方形。

生：要从1加起。

生：从1加起，连续几个奇数相加就等于几的平方。

师：同学们观察得真仔细，对，从1开始连续几个奇数相加就等于几的平方。

评析：在探究中发现，在实践中体验，是数学学习的最佳途径。在这一教学环节中，笔者特意做了三件事：一是给每个学生准备了充足的学具，每个孩子都有边长是2厘米的小正方形若干，这样便于学生动手实践，给学生创造探究的条件。二是将教材中的深红色正方形与浅红色的正方形分步摆放，并且分别用了不同的颜色区分。课件上也将摆放的过程进行分解，而不是“依教材画瓢”，给学生足够的探究空间。三是在摆放过程中组织学生“想一想”“说一说”，将学生的活动思维、表达条理化。这样的设计和组织让图形动起来，让学生动起来。学生全体投入，全心投入，探究过程生动有趣，内心的体验也就丰富多彩了。

片段三：抓住能力增长点——运用

师：其实数与形之间有着许多联系，有些特殊的数与特殊的形之间还存在着密切的联系。（展示引入时找规律填的图形，如图1）上面有图形，下面有数字，那这些数与图有什么规律呢？

生：每次都会多出一排。

生：多出来的一排总比上一排多一个。

生：都是三角形，而且是正三角形。

师：照这样的规律往下画，第5个、第6个、第7个图你能画出来吗？

（学生动手画，并计算出每个图形小圆形的总数，完成练习卡第2题，展示学生画的作品，并汇报计算过程）

师：如果不让你画，你能想象得出第十个图形是什么样子吗？会有多少个小圆形呢？

生：可以，还会是个大三角形。

生：小圆形的个数就是从1加到10的和。

生：是个大正三角形，小圆形个数只要在第7个图形的后面再接着加8加9加10就可以了。

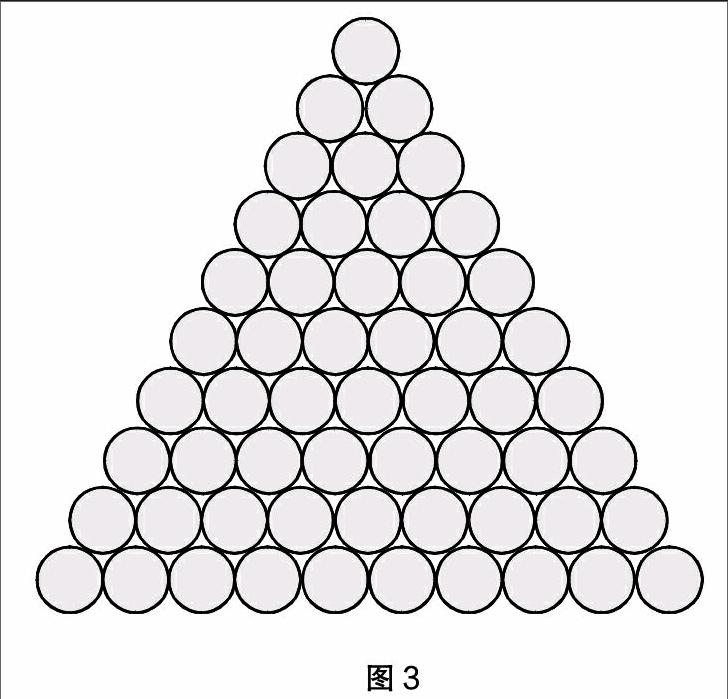
师：这些小圆形最后都拼成了一个大的三角形（如图3）。像这样的数，我们就叫它三角形数。

评析：数学思维培养的终极目标是培养有思想的学生，培养学生运用这种思想去解决问题。苏霍姆林斯基认为，真正有生命力的课堂是思考的课堂、是运用的课堂。在运用中强化意识，在运用中培养技能。

该片断教学中，学生寻找到图形排列的规律后，运用这一规律解决问题，体验进一步加深，数形结合的意识得以强化。当笔者重新展示引入部分的“找规律猜图形”，学生都踊跃发言，大胆猜想，思维的大门完全打开。

案例反思：

下课铃声响了，孩子们依然不肯离开教室。有的在稿紙上画着图形，有的在交流适于数与形的故事，有几个学生又重新找开课件，问笔者：“老师，我是这样想的……”望着他们专注的眼神，笔者的内心被深深触动：如果每一堂课都能牢牢地抓住学生的心，都能激发他们的求知欲，都能让他们感受到数学的魅力，该是一个多么成功多么幸福的事！那么，我们的责任就是尊重他们，引导他们，让学成为数学学习的主人，成为自己学习的主人。

一、备课，学生是主体

学生是课堂教学的生命线，是数学学习的主体，在积极参与学习活动的过程中不断得到发展。而数学思想的形成与发展是日积月累的，是情感与意识的浸润。《数与形》这一内容安排在人教版教材小学数学第十一册，目的是对整个小学阶段学生初步感知的数与形的思想加以归纳，提炼，并进一步渗透与强化。基于这样的出发点，笔者力求把这堂“思品课”上得形象活泼、深入浅出，让它成为一个生动传神的“例子”。这是符合小学六年级孩子身心特点的，也是符合小学生认知规律的。

本次教学设计，笔者特别注意了两个字：“趣”和“异”。

“趣”即趣味。因为像《数与形》这种课很容易变成教师的一言堂，变成优秀学生的表演场。教材上已有现成的彩色方块组图，只要引导学生看一看，想一想，说一说也可以得出结论。但仔细推敲，笔者重新设计为：把彩色方块从“1”开始拼摆，由少到多，学生先动手随意拼，接着教师再演示拼，边拼边观察，将“比一比，说一说”融于其中。这样设计，充分调动了学生的感官与思维，经历了知识形成的原始过程。

异即异步分层，对全体学生的高度关注，对不同层次学生提出不同要求。教案完成后，笔者仔细设想：哪些教学环节学生会积极主动一些？是否还可以重新设计？哪些地方学生会出现新的想法？哪些地方学生会遇到新的困难？该怎样引导？如果学生实在弄不明白该怎么办……针对这些“预设”，笔者都拟出了不同的方案。二次备课能更加有效地实施教学活动，促进学生个体的知识生成和思维生长，让数学充满生命的魅力，让数学课堂充满生机。

二、课堂，学生是主角

真正做到“以学生为本”并不容易。我们总是习惯于强硬地灌输或美其名曰“启发式”引导。这堂课，笔者虽然制作了很多课件，但在讲解时，特别注意“把问题抛给学生”，把“问”和“想”的权力给学生。在学生探究合作时，笔者将教材的主题图分步中的小方块进行拼摆展示，一步一步，水到渠成，把“做”和“想”的时间还给学生。在指导学生拼摆、比对的过程中，笔者积极参与小组的活动，和他们一起拼摆，并不急于展示结果，把“比”和“说”的空间还给学生。这样做，看起来是教师主导地位削弱了，实际上，学生的“主体”地位增强了。有效发挥主导作用的标志，是学生能够真正成为学习的主体，得到全面的发展。试想：一堂课，没有探究与思考的时间和空间，学生怎么去经历学习的过程？内心的体验从何而来？更不用说思考的权力、学习的快乐了。不担心教材内容完成不了，不担心学生弄不懂的课堂才是数学的课堂，“师生互动、生生互动”的课堂才是有生命力的数学课堂。

三、课后，学生是主人

如果一堂数学课，教师热情洋溢，学生也欢欣雀跃，课堂上满堂生花，它可能具有一定的时效性。但我们的责任是让孩子们爱上数学，用上数学，成为数学的主人。这一堂课通过直观形象的学具运用，活泼清晰地在孩子们的头脑里留下深刻印象，从形象思维上激发孩子的热情，积累了一定的数学活动经验。在“问、想、做、说、用”的过程中，抽象思维也得到发展，“合情推理”能力进一步增强。这样的课堂不但解决了目前的疑惑，又产生了新的问题：“973是一个三角形数吗？”“我看见初中的哥哥姐姐经常画图，他们专门研究图形吗？”

这样的一堂课，是中转站，是里程碑，更是数学学习的航标，是开启智慧大门的金钥匙。我希望孩子们在这样的引领和熏陶下，勇于质疑，勤于探索，感受数学思想的神奇与伟大，感受学习的成功与快乐！