夯实基础 稳步提升—由一节“一次函数复习课”引发的思考

广东省广州市矿泉中学(510400) 黄粤华

夯实基础 稳步提升—由一节“一次函数复习课”引发的思考

广东省广州市矿泉中学(510400) 黄粤华

一、教学背景

复习课是根据学生的认知特点和规律,在学习的某一个阶段,以巩固、梳理已学知识、技能,促进知识系统化,提高学生运用所学知识解决问题的能力为主要任务的一种课型.其目的是温故知新、查漏补缺,完善认知结构,促进学生解题思想方法的形成,发展数学能力.

就一个单元的复习而言,往往不是一节课可以完成的.从复习课的设计来看,可以是零散知识点的系统化整合,可以是专项题型的技巧训练、思维训练,也可以是某一个知识领域的拓展探究等,这些都有别于新授课.如何在较短的时间内,将零散的、点状的基础知识点整合好、系统化,同时又要将学生平时所学知识的疑惑点加以澄清,对所学知识的重要思想方法加以提炼,需要教师在复习课的设计和实践中加以研究.本文试着从一堂一次函数的复习课入手,谈谈在基础知识点的复习当中如何帮助学生整理知识结构,构建知识体系,提高复习效率.

二、教学设计与实施过程

活动1: 以题点知,温故知新

环节1: 下列函数中,哪些y是x的一次函数,哪些y是x的正比例次函数:

生2: 第(1)和(4)都是一次函数,因为正比例函数也是一次函数.

师: 能说说两者之间的关系吗?

生3: 一次函数解析式是y=kx+b(k/=0)的形式,当b=0时,即化为正比例函数的形式,所以正比例函数是一次函数的特殊形式,但一次函数不一定是正比例函数.

环节2: 填空(1).正比例函数y=2x的图象经过第___象限,过点(0,___)与点(1,____),y随x的增大而___.(2).一次函数y=x+2的图象经过第___象限,图像与x轴的交点坐标是___,与y轴的交点坐标是____,y随x的增大而___.

生4: 函数y=2x的图象经过第一、三象限,过点(0,0)和点(1,2),y随x的增大而增大.

生5: 函数y=x+2的图象经过第一、二、三象限,与x轴的交点坐标是(-2,0),与y轴的交点坐标是(0,2),y随x的增大而增大.

师: 能不能结合图形进行归纳说明?

生6: 板书画图说明两个函数的k值都是大于零的,所以直线从左往右上升,即y随着x增大而增大.正比例函数b值为零,所以直线经过原点,一次函数与y轴交点坐标为(0,b).

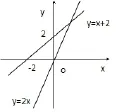
图1

环节3: 拓展研究,知识延伸

师: 能不能求这两条直线的交点坐标.

生7: 可以,如果作图标准,可以直接从图像上得出,也可以解方程组

师: 在此坐标系中是否存在与直线y=x+2没有交点的直线,如果有,需要满足什么要求,并请举例.

生8: k值相同的直线与直线y=x+2没有交点,因为此时两条直线平行,如直线y=x+1,直线y=x-2等.

师: 什么时候两个函数的值是一样?

生9: 两直线的交点就是函数值相等的时候,也就是方程组的解,即当x=2时,y=4.

师: 除了在点(2,4)相同以外呢?

生10: 从图像上看,当x＜2的时候,在点(2,4)的左边,函数y=x+2的图像在上方,此时y=x+2的函数值较大,也可以解不等式x+2＞2x;反之则是函数y=2x的图像在上方.

【设计意图】通过两组小题进行对比练习,复习一次函数和正比例函数的概念,总结函数的图像和性质,以及函数与坐标轴的交点坐标,理解直线平行的要求,理解函数与方程、不等式之间的关系.

活动2: 抓住核心,掌握基本方法

例题1已知一个一次函数经过点(3,5)和(-4,-9),求这个函数的解析式.

变式1: 已知一个一次函数,当自变量x=3时,函数值y=5;当x=-4时,y=-9,求这个函数的解析式.

变式2: 已知一个一次函数经过点(3,5),且平行于直线y=2x+3,求这个函数的解析式.

变式3: 已知一个一次函数经过点(3,5),且与y轴相交于点A,OA=1,求这个函数的解析式.

变式4: 已知一个一次函数平行于直线y=2x+3,且与y轴相交于点A,OA=1,求这个函数的解析式.

生11: 变式1和原题其实是一样的,都给出了两个点的信息,列方程组求出k值和b值就可以得到解析式了.

师: 是的,这就是本单元中非常重要的解析式求法,即待定系数法.

生12: 那其实变式2比变式1更易求解,表面上看题目只给了一个点,但是已知两直线平行,则k值是一样的,所以只剩b值待定.

关于变式3和4,学生们展开了热烈的交流,有很大一部分学生一开始都忽略了对“OA=1”的分析,通常都认为点A即(0,1).

生13: 变式3中的条件“OA=1”说明点A与原点相距1个单位长度,它的坐标可能是(0,1)或者是(0,-1),应该有两个解析式.

生14: 变式4也要进行分类讨论,而且还由平行知道k值是2.

生15: 看来,分类讨论题也不是那么难.

【设计意图】以求一次函数解析式这一典型问题为载体,展开变式训练,拉近点状知识间的距离,寻找不同问题之间的内在联系,巩固“待定系数法求一次函数解析式”,提升复习效率.

活动3: 一题多变,发散思维空间

例题2 如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C．

(1)求点D的坐标;

(2)求直线l2的解析式及C点坐标;

图2

(3)求△ADC的面积;

(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标．

(5)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标．

生16: 因为D点落在x轴上,所以它的纵坐标为0,将0带入l1可以求得坐标(1,0).

生17: 从图像可以发现l2其实经过了两个点,分别是A(4,0)和B(3,-1.5).

生18: 那△ADC的面积也很容易求的,用方程组可以先求交点C的坐标,然后纵坐标的绝对值是高,线段AD做底.

师: 很好,看来同学们掌握的都很不错,有进步!那我们再来看看变式4的问题.

生19: 存在,△ADP与△ADC有公共边AD,只要P点到x轴的距离等于C点到x轴的距离就可以了,所以P点的纵坐标和C点的纵坐标互为相反数.

因为前面进行了多个知识点的复习,所以学生在问题(5)展开了激烈的讨论,而且大部分的人一开始就猜想符合条件的E点不止一个,学生们学习的热情得到极大的提高.

生20: 当CE平行且等于AD的时候,有平行四边形,E点可以在C点左边,也可以在右边;还有一种可能是AE//DC,DE//AC,所以有三种可能.

【设计意图】此例在一个图形的背景下,做到问题的多变,将看似没有关联的知识点全部回归至同一模型架构之下进行研究,所涉及的问题与本节课开篇首尾呼应,第(4)、(5)两问加强了函数图像与几何图形之间的联系,凸显数学模型思想.

三、教学思考

《数学课程标准(2011)版)》指出,数学课程要面向全体学生,人人都能获得良好的数学教育,使不同的人在数学上得到不同的发展.由于现在各班学生的数学水平差异较大,根据课程标准的要求,在复习课的教学中,即要做到巩固基础知识,查漏补缺,又要提升学生技能,发展思维,尽量缩小生与生之间的差异.

如果在复习课中占用大量时间采用背诵、默写、齐读等方式来对概念、公式、法则进行重复和再现,复习效率必然不高,也不利于学生对所学知识的再认识和深入理解.在本节课中,笔者摒弃了传统复习课教学中常见的“练习、练习、再练习”的模式,采取层层设问,师生互动的形式,进而引发学生主动思考、归纳,逐步完成知识体系的重新构建,优化整合.

1.类比复习,梳理知识结构

学习一个由薄到厚,再由厚到薄的过程.一次函数的学习过程是由特殊到一般的过程,这其中涉及较多的概念、图形性质等方面的内容.在新授课的过程中学生普遍认为本章知识容量较大,学习起来往往顾此失彼.因此,在环节一中,通过几组类似的练习题来复习正比例函数和一次函数概念、图像性质之间的练习和区别,采取老师问,学生答的形式,不断进行拓展和延伸,同时利用图形进行直观对比,适时渗透数形结合思想,增加学生感性认识,帮助学生构建完整知识架构,增强后继复习的动机和信心.

2.变式引领,做到事半功倍

运用变式题进行教学,是初中数学常用的一种教学手段,也是培养学生思维能力,提高应变能力的一种有效方法.在教学过程中,恰当使用好变式题,会使课堂教学取得事半功倍的效果.

在环节二中,一共有5个求一次函数解析式的问题,其中第1、2两个问题的原型是教材中“用待定系数法求一次函数”例题模型,设计的目的就是定位于复习课要回归教材,回归基础,避免“题海战术”.由于有了活动一的铺垫,在变式题的练习中,学生们都能较快的动起来,甚至对于变式4这一类平时练习中较为困惑的内容,也能积极参与想到解题思路和解题办法,说明这种密台阶、低起点的复习设计,在完成了基础知识体系构建的情况下,能够达到较理想的复习效果.

3.由点及面,发展思维空间

英国国家数学课程强调开放性问题的作用,要求变封闭问题为开放问题.在数学教学中,只要把封闭问题加以改良,那就会使的教学变得更加有趣、富有挑战性.在例3中虽然设计了多达5个问题,但是每一个都较为容易上手,学生在学习的的过程中能够自然的体会到其中内涵,在这种由浅入深、由易到难,循序渐进的编排设计中,学生的复习效果会呈螺旋式递进,同时原有的知识结构也会在复习的过程中进行优化重组.犹如一间堆满杂物的仓库被重新整理摆放后一样,遇到需求的时候要什么则拿什么,一个是效率的提升,另外这样复习也能逐步深化学生对知识的理解,形成解题技巧,同时生成数学思维,发展数学思考能力.

[1]孔凡哲.新课程典型课案例与点评.东北师范大学出版社.2003

[2]马复.设计合理的数学教学.高等教育出版社.2003

[3]茅雅琳.“课堂让学”理念下的课堂评析[J].中国数学教育(初中版), 2015(4): 33-36

[4]刘海涛.初三数学课堂针对学生差异的有效训练[J].中国数学教育(初中版),2015(6): 19-23

[5]张爱平.经历过程渗透思想发展能力[J].中国数学教育(初中版), 2015(6): 35-38

[6]陈文娣.加强数学思想引领注重教学过程优化[J].中国数学教育(初中版),2015(6): 39-42