让“化归”成为开启数学的金钥匙*—初中数学教学中渗透化归思想的策略

广东省佛山市南海区和顺第一初级中学(528241) 李西华

让“化归”成为开启数学的金钥匙*—初中数学教学中渗透化归思想的策略

广东省佛山市南海区和顺第一初级中学(528241) 李西华

匈牙利著名数学家P.罗莎(Rozar,Peter)在《无穷的玩艺》中写道: “数学往往不是对问题进行正面攻击,而是不断对它进行变形,直到把它转化成能够解决的问题”.前苏联数学家雅诺夫思卡娅说: “解题――就是意味着把所要解的问题转化为已经解过的问题.”在初中数学中,有许多新知识的获得或新问题的解决都是通过转化为已知知识或已解决的问题来完成的,也就是将新知识向已知知识点或知识块转化,从而使问题得到解决.解决某些数学问题时,如果直接求解较为困难,可通过观察、分析、类比、联想等思维过程,运用恰当的数学方法进行变换,将问题转化为一个新问题(相对来说较为熟悉的问题),通过新问题的求解,达到解决原问题的目的.这一思想方法我们称之为“化归的思想方法”.化归思想,就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化,进而达到解决的一种方法.一般总是将复杂问题通过变换转化为简单问题;将难解的问题通过变换转化为容易求解的问题;将未解决的问题通过变换转化为已解决的问题.化归的基本功能是: 生疏化成熟悉,复杂化成简单,抽象化成直观,含糊化成明朗.化归思想是中学数学最基本的思想方法,是一切数学思想方法的核心,画如下结构图学生易于理解:

图1

皮亚杰说过: “一切有成效的工作必以兴趣为先决条件.”兴趣是最好的老师,是学生积极创造的驱动力,是创造思维活动的成功先导.为了提高学生学习化归思想的兴趣,对于初学者,老师也可以讲“曹冲称象”、匈牙利著名数学家P.罗莎的“数学家烧开水”等典故来阐述数学化归思想方法及其功用.下面主要从渗透化归思想的策略方面进行研究.

一、寻找渗透化归思想的孕育点

数学思想教学要经历多次孕育阶段.学生学习数学思想存在潜意识性,潜意识的作用是缓慢的、渐进的,所以要反复孕育,而且对于复杂的、难度较大的思想方法,孕育的次数也相应多些.(以初三为例)例如(1)一元二次方程转化为一元一次方程;(2)相似多边形的性质: 周长的比、面积的比化归为相似比来解决;(3)三角形的中位线定理的证明问题化归为特殊四边形中的问题来解决;(4)相似三角形问题: 通过作辅助线,把相似三角形中的一些问题化归为基本图形,A型、X型、母子型等来解决;(5)将多边形内角和问题化归为三角形内角和问题;(6)将特殊四边形问题化归为全等三角形问题;(7)将相似三角形问题化归为对应线段成比例问题;(8)将四边形四边中点问题化归为三角形中位线问题等等.

例三角形的中位线定理的证明问题化归为特殊四边形中的问题来解决.

八年级学习了平行四边形的性质和判定及三角形全等的性质和判定.

①确定目标: DE//BC,且DE=BC=⇒平行四边形?(原因: 平行四边形的对边平行且相等)

②寻找差异: 无法直接找到平行四边形.

③消除差异: 按如下图添加辅助线,构造平行四边形,易得解.

再如初中数学“有理数的减法”,教材是通过学生自主探究和合作交流,经历把有理数的减法转化为加法的过程,从而得出“减去一个数等于加上这个数的相反数”,这个地方虽然很简单,但却充分体现了把“没有学过的知识”转化为“已经学过的知识”来加以解决,学生一旦掌握了这种解决问题的策略,今后无论遇到多么难、多么复杂的问题,都会有意识想到把“不会的”转化为“会的”知识来加以解决,这符合学生原有认知规律,作为教师,我们不能因为简单而忽视它的教学,实践告诉我们,往往是越简单、浅显的例子,越能引起学生的认同,所以我们不能错过这一绝佳的渗透化归思想的机会.

总之,数学思想是数学的精髓.作为数学老师,深度钻研教材,充分挖掘内隐的数学思想,采取有效的策略,使之显化于教学之中,“流淌”在数学课堂之内外.

图2

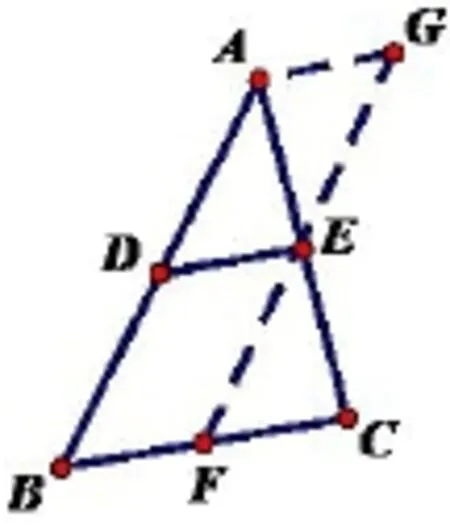
图3

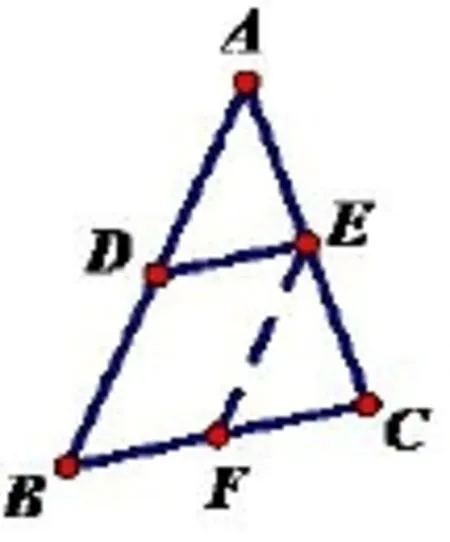
图4

图5

二、在慢化教学中渗透化归思想

慢化教学是针对学生的认知特征和学习水平而采用的有效性过程,从而等待学生领悟的实用性教学理念,其目的是借助慢化教学的平台让学生有角度切入、有时间思考,能听得懂、学得会,进而从学会到想学、会学、乐学.慢化教学不是为慢而慢,更不是消极怠工,而是为了生成“快”的效果而采取的“缓慢”策略,其最终目的是为学生提供更为广阔的、更为自由的、更为适切的学习空间.

例: 证明: 如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半.

已知: 在Rt△ABC中,∠ABC=90°,D是斜边AC上的中点.

老师布置上课的前一天晚上先预习,接着课堂上让学生进行小组讨论,为了使学生更易于了解、领悟、内化数学化归思想,笔者采用慢化教学中渗透化归思想的策略,取得了较理想的效果.

三、渗透常见的化归方法

化归思想方法用在研究、解决数学问题时,思维受阻或寻求简单方法或从一种状况转化到另一种情形,也就是转化到另一种情境使问题得到解决,这种转化是解决问题的有效策略,同时也是成功的思维方式,初中阶段常见的化归方法有:

(1)直接转化法: 把原问题直接转化为基本定理、基本公式或基本图形问题.

例 如: 如图,已知 菱 形BEDF内接于△ABC,点E、D、F分别在AB、AC和BC上,若AB=15,BC=12,求菱形的边长.

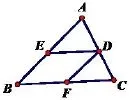
图6

分析: 通过利用菱形的四边都相等,对边平行的性质,把求菱形边长的问题直接转化为证一对基本图形(A字形)相似的问题,即△AED∽△ABC,再利用相似三角形的性质对应线段成比例求出菱形的边长.

(2)换元法: 运用“换元”把式子转化为有理式或使整式降幂等,把较复杂的函数、方程、不等式问题转化为易于解决的基本问题.

(3)数形结合法: 研究原问题中数量关系(解析式)与空间形式(图形)关系,通过互相变换获得转化途径.

例如: 二次函数与一元二次方程的关系

图7

建立如图所示思维导图,通过“数”与“形”的互相转化、“特殊”与“一般”的转化,很好的揭示了二次函数与一元二次方程的关系,使学生易于理解.

(4)等价转化法: 把原问题转化为一个易于解决的等价命题,达到化归的目的.

例如：如图,在Rt△ABC中,E为斜边AC上一点, AE=2,EC=1,四边形DEFB为正方形,则阴影部分的面积为___.

分析: 将直角三角形EFC绕E点,按逆时针方向旋转,因为BDEF是正方形,所以EF和ED重合,C点落在BD上,阴影部分的面积转化为直角三角形AGE的面积,因为AE=2,EC=1,所以阴影部分的面积易求得为1.

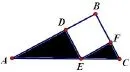
图8

图9

图10

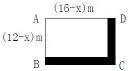
图11

(5)特殊化方法: 把原问题的形式向特殊化形式转化,并证明特殊化后的问题、结论适合原问题.一般问题特殊化,使问题处理变得直接、简单.特殊问题一般化,可以使我们从宏观整体的高度把握问题的一般规律,从而达到成批的处理问题的效果.

(6)构造法: 构造法就是根据题设条件或结论所具有的特征和性质,构造满足条件或结论的一个合适的数学模型,把问题变为易于解决的问题.

例如: 解非特殊角的三角函数问题: 求tan22.5°的值.

解: 构造如图所示的Rt△ABC,∠C=90°,设AC= DC=1,则延长CD到B,使则

图12

分析: 本题从22.5°是45°的一半着手思考,从大脑储存库里调运出特殊三角形等腰直角三角形的其中一个底角是45°想到构造一个等腰直角三角形,通过延长再构造一个以等腰直角三角形的斜边为腰的等腰三角形,它的底角即为22.5°,从而把“数”的问题向“形”的问题转化,顺利得解.

四、用不同呈现方式渗透数学化归思想

(1)要素化式: 确定化归对象,确定化归目标,寻找差异,确定化归方法,消除差异.特点是具体、明了,学生易懂,适合方程、方程组、不等式等内容的教学.

(2)结构图式: 结构网络化,条理清晰,直观、易懂,适合方程、方程组、不等式、几何证明等内容的教学以及教学小结、反思.

例2: 解方程组:

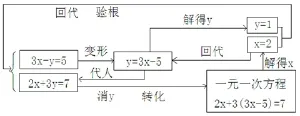
图13

五、教会学生进行解题后的反思

罗增儒教授认为反思就是从自身的认识活动中“脱身”出来,作为一个“旁观者”来看待自己刚才做了些什么事情,使自己的活动成为了思考的对象.有两个层面的回顾反思,一个是解题层面的回顾反思(已高度关注),另一个是学会解题层面的回顾反思(想知道很多又有很多不知道).教师可以教会学生从以下几方面进行反思: ①体现了哪些数学思想方法?②用到了哪些数学知识?③存在哪些困难?④解法有没有可以改进的地方?⑤积累了哪些数学活动经验?⑥你能否把这一方法用于其它问题?等等.

六、给学生一个化归思想的“创客”空间

启迪智慧,开拓想象空间,快乐学习,智慧人生.给学生一个数学思想的“创客”空间,学生会给你一个意想不到的结果.比如在“创客”空间里让学生尝试挖掘数学课本中隐含化归思想的例题、习题解题思路、定理的证明方法;网上搜索有关化归思想的学习文章、隐含或运用化归思想的题目;小组合作尝试编制有关数学思想方面的简单小题目;小组评选数学思想研究“小专家”,带领自己的研究团队来了解、认识数学思想,进而领悟、研究数学思想;每小组在“小专家”带领下开展数学思想“一帮一”活动;每周由一个小组简单汇报本小组的数学思想研究的情况;定期在宣传栏展示学生的优秀研究成果,定期举办交流分享活动,你可以聆听别人的分享和经验,也可以分享自己的创意,展示自己的作品,招募小伙伴一起实现创意.如下是学生在化归思想的“创客”空间的部分作品.

学生学习数学不仅要学习它的知识内容,更要学习它的精神、思想和方法.为此,在数学教学中,要善于挖掘教材中蕴含的化归思想方法,不断总结化归法解题的一般原理、提炼蕴含其中的思想方法,把化归思想方法的教学融于各个环节之中,让学生切实感受到化归思想方法的存在形式及其发挥的作用;还要特别强调解决问题以后的“反思”,因为在这个过程中提炼出来的数学思想方法,对学生来说才是易于体会、易于接受的;更要注意渗透的长期性,因为数学思想方法是在启发学生思维过程中逐步积累和形成的,数学思想方法在教学中的渗透必须经过循序渐进和反复训练,才能使学生真正地有所领悟.

*本文是董磊主持的广东省教育科学“十二五”规划2011年度立项课题“如何在初中数学教学中渗透数学思想方法的实践研究”(课题批准号: 2011TJK014)的研究成果之一.