巧探数列通项公式
王 琳
(山东省青岛职教教研室,266023)
巧探数列通项公式
王琳
(山东省青岛职教教研室,266023)
数列通项公式深刻揭示了数列各项与项数之间的内在关系.通项公式的探求对研究数列至关重要,可以说是数列的灵魂.在具体问题中,数列特点不同,其通项公式的探求方法也不尽相同.
一、观察法
根据所给的一列数,通过观察、分析,找出其变化规律,从而探求其通项.
例1设数列{an}的前5项分别是图1中5个图形的点的个数,试猜想该数列的一个通项公式.
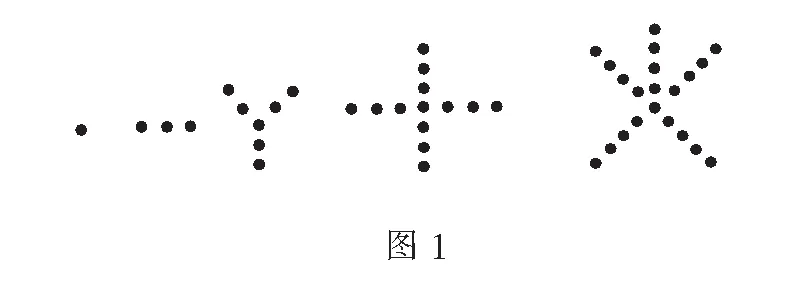
本题给出的一组图形非常有特点:
第一组点的个数a1=1:可以看成
a1=0×1+1;
第二组点的个数a2=3:可以看成
a2=1×2+1;
第三组点的个数a3=7:可以看成
a3=2×3+1;
第四组点的个数a4=13:可以看成
a4=3×4+1;
第五组点的个数a5=21:可以看成
a5=4×5+1;
……
通过观察,分析,可得
该数列的一个通项公式为
an=(n-1)n+1.
二、定义法
根据定义判断数列是等差数列或等比数列,从而用公式求通项.
例2在数列{an}中,已知a1=1,a2=3,an+2=3an+1-2an,n≥2且n∈Z*,求证:数列{an+1-an}是等比数列,并求数列的{an}的通项公式.
解∵an+2=3an+1-2an,
∴an+2-an+1=2an+1-2an,
即an+2-an+1=2(an+1-an),
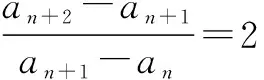
所以数列{an+1-an}是公比q=2的等比数列.
设an+1-an=bn,则数列{bn}是一个公比为2的等比数列,其中b1=a2-a1=3-1=2,
所以bn=b1·qn-1=2×2n-1=2n,
即an+1-an=2n.
再解决如下问题:在数列{an}中,a1=1,an+1-an=2n(n∈N*),求an.
n=1时,a1=1,n≥2时,
a2-a1=2,
a3-a2=22,
a4-a3=23,
……
an-an-1=2n-1.
以上n-1个等式累加,得
an-a1=2+22+…+2n-1

故an=2n-2+a1=2n-1,且a1=1也满足该式,
∴an=2n-1(n∈N*).
三、前n项和法
利用公式an=Sn-Sn-1(n≥2)求通项.有些数列给出{an}的前n项和Sn与an的关系式Sn=f(an),利用该式写出Sn+1=f(an+1),两式作差,再利用an+1=Sn+1-Sn导出an+1与an的递推式,从而求出an.
例3已知各项均为正数的数列{an}的前n项和为Sn满足S1>1,且6Sn=(an+1)(an+2)n∈N*,求{an}的通项公式.
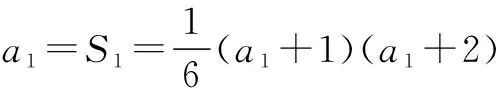
由已知a1=S1>1,因此a1=2.
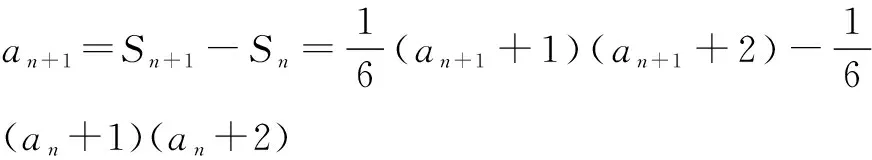
(an+1+an)(an+1-an-3)=0.
∵an>0,∴an+1-an=3,
从而{an}是首项为2,公差为3的等差数列,故{an}的通项为
an=2+3(n-1)=3n-1.
四、累加法
形如an-an-1=f(n)(n=2、3、4…)且f(1)+f(2)+…+f(n-1)可求,则可用累加法求an.有时若不能直接用,可变形成这种形式,然后用这种方法求解.
例4在数列{an}中,a1=1,an-an-1=2n-1(n=2、3、4、…),求{an}的通项公式.
解n=1时,a1=1.
n≥2时,a2-a1=3,
a3-a2=5,
a4-a3=7,
……
an-an-1=2n-1.
这n-1个等式累加,得
an-a1=3+5+7+…+(2n-1)
=n2-1.
故an=n2-1+a1=n2,
∴通项公式是an=n2(n∈N*).
五、累乘法
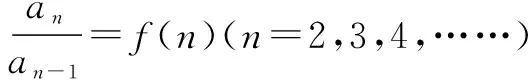
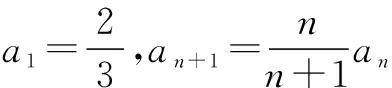
分别令n=1,2,3,…,(n-1),代入上式得n-1个等式,累乘,得
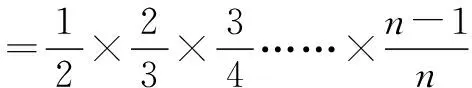

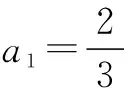

六、构造法
1.构造等比数列法
原数列{an}既不是等差数列,也不是等比数列.若把{an}中每一项添上一个数或一个式子后,能使之成为一个等比数列,则可求出an.该法适用于递推式形如an+1=ban+c或an+1=ban+f(n)或an+1=ban+cn,其中b、c为不相等的常数,f(n)为一次式.
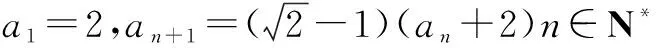
解构造新数列{an+p},使之成等比数列.
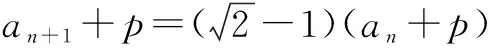
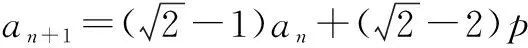
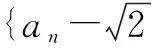
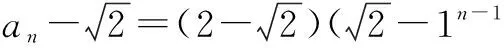
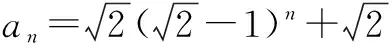
例7已知数列{an}中,a1=1,an+1=2an+3n,求数列的通项公式.
分析此问题不同于例6,该数列中含3n是变量,而不是常量了,故应构造新数列{an+λ·3n},其中λ为常数,使之为公比是an的系数2的等比数列,
解构造数列{an+λ·3n},λ为不为0的常数,使之公比成为q=2的等比数列.
即an+1+λ·3n+1=2(an+λ·3n),
整理得an+1=2an+(2λ·3n-λ·3n+1),
与题设等式比较得λ=-1.
新数列{an-3n}是首项为a1-31=2,q=2的等比数列,
∴an-3n=-2×2n-1,
∴an=3n-2n.
2.构造等差数列法
如果数列{an}既不是等差数列,也不是等比数列,但具有递推关系式形如an+1=ban+bn+1+f(n),那么可以把两边同除以bn+1后,想法构造一个等差数列,从而间接求出an.
例8数列{an}满足an+1=-2an+(-2)n+1(n∈N*),首项为a1=-2,求数列{an}的通项公式.
解an+1=-2an+(-2)n+1,
两边同除以(-2)n+1,得

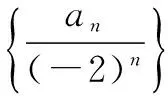
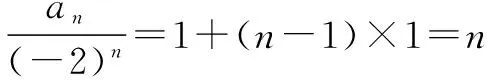
故an=n(-2)n.
对数列通项公式的探求,除了以上几种方法外,还有根据递推关系式求通项、取倒数等方法,可谓曲径通幽,其乐无穷.限于篇幅,本文不再一一举例说明.

