一道不等式问题的解法赏析

孙成亮　　　　　　　　　　周成刚

(安徽省萧县鹏程中学，235200)　(安徽省濉溪县孙疃中学，235121)



一道不等式问题的解法赏析

孙成亮周成刚

(安徽省萧县鹏程中学，235200)(安徽省濉溪县孙疃中学，235121)

求解不等式问题在高考和奥赛中经常遇到.这类问题的解决经常涉及到很多知识点的融合,也容易培养学生的能力.换元,放缩,函数与方程思想等在解决不等式问题中经常会有体现．本文通过一道不等式问题的几种解法感受一下各种思想在不等式问题中的灵活应用．

题目求证:(1+x)n+(1-x)n<2n,其中|x|<1,n≥2,n∈N.

该题是一道不等式的证明问题,根据题目的构造,感觉形式不算很难，比较容易想到的是数学归纳法．

证法1(数学归纳法)

∵|x|<1,n≥2,n∈N.

(1)当n=2时,不等式左边=(1+x)2+(1-x)2=2+2x2<4=22,不等式成立

(2)假设n=k(k≥2)时命题成立,即

(1+x)k+(1-x)k<2k.

那么n=k+1时,则

(1+x)k+1+(1-x)k+1

=(1+x)k(1+x)

+(1-x)k(1-x)

(*)

=(1+x)k+(1-x)k

+(1+x)kx-(1-x)kx

=2k+2k=2k+1,

∴n=k+1时不等式成立.

综上可知(1+x)n+(1-x)n<2n,|x|<1,n≥2,n∈N都成立.

评注上述方法中(*)式可以处理得更简单,步骤如下:

∵1+x<2,1-x<2,

∴(1+x)k(1+x)<2(1+x)k,

(1-x)k(1-x)<2(1-x)k.

∴(1+x)k+1+(1-x)k+1

=(1+x)k(1+x)+(1-x)k(1-x)

在该题的解法中我们发现用到了二项式定理,那么是否可以直接用二项式定理解这道题目呢?

证法2(1+x)n+(1-x)n

=2·2n-1=2n.

故不等式成立.

证法3(三角换元)

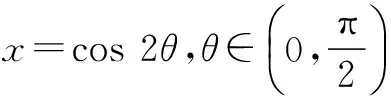
高速公路桥梁的加固维修养护需要专业的人才来执行，桥梁的加固维修养护工作比较单调乏味，工作人员普遍工作积极性不高，这样很难保证桥梁的加固维修养护工作，因此要不断加强专业的加固维修养护人才队伍，组织培训相关人才专业技能，提高工作人员的责任心和专业技能，更好地为高速公路桥梁的加固维修养护贡献自己的力量。

1+x=1+cos 2θ=2cos2θ,

1-x=1-cos 2θ=2sin2θ，

∴(1+x)n+(1-x)n

=2n(cos2nθ+sin2nθ)<2n.

不等式成立.

评注观察1+x,1-x形式很容易联想到三角函数里面的二倍角公式,且|x|<1又正好符合这种情况，所以这种方法看起来似乎意料之外,其实是在情理之中.

证法4(利用函数性质)

令f(x)=(1+x)n+(1-x)n,|x|<1,则f(-x)=f(x),所以f(x)为偶函数.

不妨设0≤x<1,则

f′(x)=n(1+x)n-1-n(1-x)n-1

=n[(1+x)n-1-(1-x)n-1].

∵1+x>1-x>0，

∴(1+x)n-1>(1-x)n-1，

∴f′(x)>0,

∴f(x)在区间[0,1]上为增函数,

∴f(x)

根据偶函数性质知该待证不等式成立.

评注函数与方程思想是一种重要的数学思想,构造偶函数再利用求导使这一道题轻松地得到解决.本解法另辟蹊径,为解题提供了另外一条出路.

证法5(整体换元)

令1+x=a,1-x=b,则

0

所以原不等式变形为证明

an+bn<(a+b)n,n≥2.

上面这个不等式中，因为n≥2,所以右边展开至少有4项.

所以原不等式成立.

评注证法2用到了二项式定理,证法3用到了三角换元,这种方法是把换元思想和二项式定理巧妙结合,使该题轻松地得到了解决.