高中数学反思性教学研究

徐　磊

(江苏省启东市吕四中学，226241)



高中数学反思性教学研究

徐磊

(江苏省启东市吕四中学，226241)

现代教学中强调“学会教学”“学会学习”．这需要进一步在教学中发挥主观能动性,要求教师对教学进行反思,以此推动在教学过程中不断发现、思考与总结问题,从而推动教学过程不断优化．虽然反思性教学在高中数学中得到运用,但是教师在理解上仍存在不少误区,以致于直接影响了效果．这里，笔者结合实践,重点在教与学两个方面对反思性教学进行探讨,以便参考．

高中数学教学,教师是反思的主体,其反思也应该贯穿于整个教学过程,不仅仅包括教学,还包括备课、提问以及作业设计等等.通过反思，寻找最佳教学途径,推动学生自己发现问题、思考问题与解决问题,以达到全面提高学生素质的目的．

一、对教学目标进行反思

目标是一切教学的基础．针对高中数学反思性教学,首要的是对教学目标进行反思.教学目标既要结合新课标理念,又要契合文本内容以及学生实际．教师需对教学目标进行反思,预定学生学习成效,继而不断完善总结出科学的教学目标,并以此展开有效教学．

比如，针对“集合”内容的教学,传统教学中出于应试教育考虑,教师对目标制定比较功利,只关注学生成绩以及应付考试．因此，在教学中大多采用灌输,直接给学生机械讲解集合、子集的含义,等等.至于巩固更简单,通过大量机械训练,提高学生应试技能．虽然这也有效,但这是在牺牲学生大量时间的基础上进行的,没有从学生实际出发．数学这一学科由初中到高中的知识跨度明显增大,对学生的抽象思维要求要比初中高得多,高一学生学习数学还处于初高中知识衔接阶段,所以讲解集合知识应先从生活实例出发,引导学生从生活中建立“集合”概念,让学生去思考并在课堂上分享自己所知道的生活中的集合．例如，一个教室中的所有人是一个集合,那么这间教室中的每一个人都是这个集合的元素,所有学生构成的集合就是这个集合的子集．引导学生从生活中找“集合”,无疑是让学生体会学习“集合”概念的最佳方法．

笔者经过前后对比,反思,发现对于高中数学来说,固然知识传授重要,但是更要遵循新课程目标,为学生学会学习、提升数学综合素质奠定基础．传统教学是为了应付考试,但却有点急功求利,在目标制定上不够科学.因而笔者经过反思,前后对比,重新制定目标,突出引导学生进行有意识自主探究,这样不仅可以有效提升课堂实效,而且还能提升学生综合素养，一举两得．

二、对教学方法进行反思

当前传统教学方法已经不能适应教学需求,学生、家长对之反映较大,甚至还有部分学生产生抵触情绪．对此进行反思,笔者认为需要结合新课标,从学生实际出发,逐步完善其教学方法．

首先,教师需要认识到教学方法有没有效,直接影响着课堂教学的成效．对于高中学生来说,他们已经有了一定的自学能力,因而教师需要做的是引导学生学会学习,并在过程中能够获得其方法,提高其能力,而不简单是知识灌输．其次，教师还需要考虑学生接受能力,情感态度与价值观,等等.尽可能通过外在方法激发学生兴趣,调动他们内在的主观能动性,在有效提高学生参与率的同时彰显其主体地位．

以“函数的概念和图象”这一教学为例,教师先把学生按照一定的标准分成若干小组,再引导学生结合具体函数自主探究函数概念和图象,如指数函数、幂函数以及对数函数，等等.继而引导学生通过小组合作进行交流探讨,让学生在小组中分享自己收获,并对自己疑问进行再次探讨,从而推动对具体问题进一步解决．

与传统教学方法进行比较,小组合作学习方法不仅适应了学生需求,改变了传统灌输教学模式,彰显了学生主体地位,发挥了其主观能动性．同时，将学生进行分组,在形式上也进行了创新,能够有利于学生在宽松环境中进行自由讨论,从而达到活跃课堂,生成精彩的最终目的．

三、对教学对象进行反思

时代在发展,同样学生也在发展,况且现在学生大多是独生子女,其个性特征更加明显．而教学效果最终还需要在学生身上体现，鉴于此学生的态度,内在的学习动力更加重要．因而教师在进行反思性教学时,更需要关注教学对象,只有教师认识到学生的主体地位,并且能够根据学生实际有针对性制定教学目标计划，改进教学方法,才能推促教学生成精彩．对此,笔者曾提出分层教学理念,即分析学生个性差异的基础上有针对性制定不同层次的学习目标,并对此进行不同层次的教学方法,继而进行引导,从而有效推促目标生成．

比如，在数列学习过程中,笔者就曾根据学生学习基础、能力把全班学生分为三个层次,分别代表不同的学习能力．第一层次学生处于班级“尖端”,他们数学基础较好,理解能力、逻辑思维以及创新能力较强,对于新知识接受快,能灵活运用．对教材中常识性、基础性知识往往已经不能适应他们的需求,或者不能满足其求知欲望．对等比数列和等差数列,笔者将高考中较难的相关题目发给第一层次的学生,让他们进行自主探究．对于第二层次学生来说,基础与能力相对较弱,但是对学习具有一定的信心,因而笔者帮助他们对基础知识进行强化巩固,通过一定量的训练,有效提升他们能力,让他们能够迅速达到第一层次．对此,笔者针对基础题目训练完成后,往往布置一些具有难度的思考题,引导他们全面理解和整合基础知识,在解决具体问题过程中获得成功体验,并能享受学习,继而进一步巩固学习信心．对于第三层次的学生来说,他们往往基础比较薄弱,理解有一点困难,对他们最适合的方法就是夯实基础,强化基本能力训练,并且突出其兴趣培养．对此，教师可以创设情境,搭建平台,引导学生掌握基本概念，理解基础知识，学会基本方法,等等.教师可以利用学生生活知识有效降低学习难度,把抽象知识变得生动、具体,在加深学生理解的同时,有效激发他们学习兴趣．

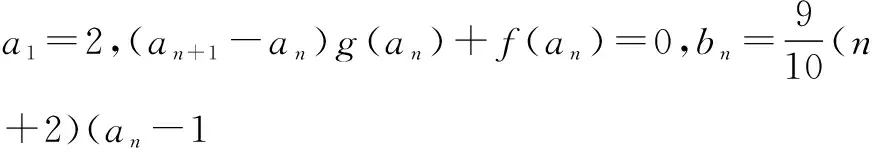
(1)求证:数列{an-1}是等比数列;

(2)当n取何值时,bn取最大值,并求出最大值.

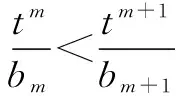
该例题的三小问难度递增,对于基础薄弱的同学,教师需要引导其掌握证明等差或等比数列的基本方法;能力中等的同学须掌握第(2)问求最值的多种方法;而对于拓展性较强的第(3)问,需鼓励基础扎实、思维能力较强的同学探究多种解题方法．

教学活动不仅仅关系教师,更多关系学生接受理解．因而教师在教学过程中,除了自身反思外,更多需要引导学生进行反思,包括学习方法,学习态度,以便引导学生总结学习经验,不断优化学习内容．

比如函数学习中,少数学生往往漏掉条件,或者在解题过程中会浪费大量时间．这时教师需要引导学生进行反思,为何为会漏掉条件?由于函数问题比较抽象,加之条件较多,因而导致做题过程中漏掉条件;再进一步反思,则会发现最根本原因就是在学习中缺少行之有效的学习方法,继而导致在解决函数问题中出现差错．

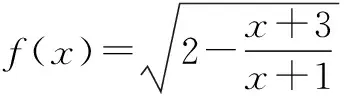
(1)求A;

(2)若B⊆A,求a的实数范围.

分析求定义域是解决函数问题的基本条件,所有学生都知道根号下的整体须不小于0,但仍会有一小部分学生粗心大意、急于求成,忘记分母不等于零的条件,不考虑x≠-1的情况．虽然最后求出的定义域中不一定会有体现,但考虑全面是非常必要的．

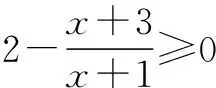
x≤-1或x≥1.

又x≠-1，

∴A=(-∞,-1)∪[1,+∞).

(2)由(x-a-1)(2a-x)>0,得

(x-a-1)(x-2a)<0.

∵B⊆A,∴2a>1或a+1≤-1,

∵a<1,

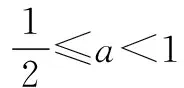
对于学生来说,由于课堂时间有限,因而更多反思需要集中在课后去完成．具体来说,教师需要通过引导学生反思方法以及效果,并且结合自我检查,反馈,总结,以便寻找最优学习方法,最终促成其精彩生成．

同样是等差数列,教师可以引导学生进行自我反思：本节内容是该章节的第一课,从知识衔接来看,具有承前启后作用.从学习内容来看,主要是学习一些基本知识与技能,认识一些概念,比如等差数列以及其通项公式的推导过程;从学习方法来看,主要是培养学生总结、分析乃至推理等综合能力．在学生反思过程中,发现学生基本上能够理解和掌握等差数列概念以及具体公式,同时还能运用等差数列基本性质,能够比较灵活转化之间关系,课堂气氛也相对活跃．对于数列通项公式，主要是寻找各项随项序的变化规律，对此学生已经解决过类似的规律性问题,因而学习比较轻松,并且能够主动探究,借助其定义推导出通项公式．在教学过程中,学生通过自主预习,合作探究等形式推促课堂教学任务顺利完成．笔者认为,引导学生反思,最主要的给学生目标,引导学生对照学习效果,并且进行反思,继而反馈在以后的学习过程中,以便优化学习方法,提高学习效率．

所以，在日常学习中,教师需要引导学生有意识地运用数学方法,并且逐步巩固,继而成为个人学习方法，这是其一．其二通过方法还能有效引导学生纠正过去学习中存在的问题,以便优化其效果,最终提升学习能力．还有,教师针对一些考试成绩不佳,但是学习能力较好的学生,这就需要教师引导他们反思在考场中失误在何处,继而让学生认识到也许是学习态度,或者粗心导致失分.只有这样反思,才能有意识引导学生,让学生获得全面发展．

总而言之,对于教学来说,教师对教学进行反思以及引导学生进行反思,是高中数学发展的趋势,同样也应该引起教师高度重视．当然,对于其反思性教学还有许多需要解决的问题,这需要教师之间进一步交流,以便推促高中数学教学改革,继而真实提高课堂实效．