类比引领 探究生成——以“圆锥曲线”的教学为例谈类比思维能力的培养

陶　蕊　谈玉琴

(浙江省海盐元济高级中学，314300)



类比引领探究生成
——以“圆锥曲线”的教学为例谈类比思维能力的培养

陶蕊谈玉琴

(浙江省海盐元济高级中学，314300)

新课标指出，数学能力的核心是思维能力,类比思维能力是思维能力的具体体现．在平时的学习中,我们用类比的思想可以轻松地发现新的结论或命题,圆锥曲线的学习就是一个很好的例子．本文以圆锥曲线为例浅谈类比思维能力的培养．

数学教育家波利亚说:“类比是一个伟大的引路人”．数学史上有许多数学家通过类比发现了许多重要的数学结论．在数学教学与研究中,类比是进行合情推理的一种非常重要的思维方法,高中数学新课程也已经将类比推理能力的培养作为课程目标之一,在近几年的高考中也大量出现类比题．把课本内容有效整合,进行类比教学,可以提高效率,开拓学生的视野,提高创新思维．由此可见，类比在教学中的作用不可低估.我们应在日常教学中有意识地教会学生用类比的方法探究问题,发展学生的类比思维．

一、用类比架设温故求新的桥梁,激发类比意识

建构主义认为,学习是学习者以自身已有知识和经验为基础的主动的建构活动,不应被看成对教师所授知识的被动接受．在教学活动中,教师应抓住知识的最近发展区,引导学生主动参与探究过程,形成良好的数学认知结构．如，概念、定义、定理的导入,常可以从问题在知识体系中的地位、与原有知识的内在联系,从学生原有认知结构出发提出新的问题,引导学生类比探究,实现有意义的知识建构．

案例1在双曲线定义的教学中,笔者尝试引导学生类比椭圆的定义自主探究，引入双曲线的定义.

(1)复习回顾:椭圆的定义是什么?

(2)质疑激发探究欲望:椭圆的定义中的“和”字,你会想到什么?学生自然联想到“差”字,即平面内与两个定点的距离之差等于常数的点的轨迹是什么曲线呢?

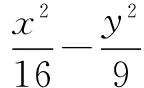
(4)画曲线:类比椭圆的性质研究,很快学生就作出了双曲线的大致图形．并能够联想到反比例函数．

(5)完善双曲线的定义：教师可以进一步引导学生思考下列问题:

(i)满足|PF1|-|PF2|=8的点的轨迹就是上述曲线吗?学生思考后得知,只有右支上的点满足条件；

(ii)左支上的点满足什么条件呢?取特殊点A(-4,0)检验，学生计算并得AF1-AF2=-8；

(iii)教师引导启发:右支上的点满足|PF1|-|PF2|=8,左支上的点满足|PF1|-|PF2|=-8,那么应该如何定义双曲线呢?

(6)给出双曲线的完整定义．

心理学研究表明:当学习内容处于学生的“最近发展区”范围之内时学生更容易获得成功.这种成功感可以有力地保证学生不会因过多的失败而放弃他们的努力, 失去发现的机会．同时,应用类比法,可以促使学生回顾旧知，尝试在已有知识的基础上去发现新结论、构建新知识, 可以有效地实现旧知识在新内容中的正迁移,帮助学生建立新旧知识的联系，突破教学难点、降低教学难度．由此可见，在讲授新知识的同时,要经常联系旧知识,创造条件进行类比,扩展学生的思路,养成学生进行类比推理的习惯．通过这样新旧知识的联系来进行类比,既有利于理解、掌握新知识,还能使旧知识得到巩固,同时拓宽视野,有利于培养学生的类比思维能力．

二、巧借类比，探究性质,培养类比思维能力

波利亚还说过:“类比就是一种相似．”把两个数学对象进行比较,找出它们相似的地方,从而猜测这两个数学对象的其它一些属性也有类似的地方,这是关于概念、性质的教学中最常用的方法．

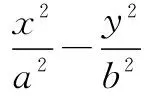
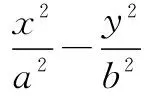
证明设点M、P的坐标为(m,n)、(x,y),则N(-m,-n).

因为点M，P在已知双曲线上,所以

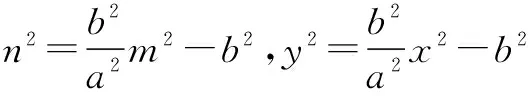
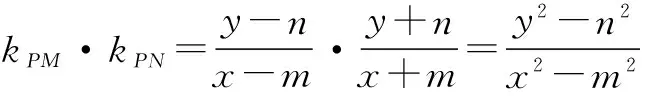
本案例引导学生运用类比的思想推导出双曲线的性质,然后再让学生类比椭圆性质的证明方法加以证明,验证类比出来的结论的正确性.这有利于培养学生严谨的学习习惯,同时也是放手还课堂给学生,让学生体验类比探究发现的过程,并在此过程中动手,动脑,感受成功的喜悦，体验学习数学的快乐．类比是重要的学习迁移能力,通过对椭圆和双曲线类比分析,帮助学生发现它们有很多相似的地方,可以用相同的方法来处理问题,开阔了解题的思路,增强思维灵活性,促进类比思维能力的提高．

三、在解题教学中加强类比训练,促进学生类比思维的发展

康德说过:“每当理智缺乏可靠论证的思路时,类比这种方法往往能指引我们前进．”因此只要学生学会了类比这个重要的思想方法,不仅能帮助他们理解和掌握新知识,而且还能提高他们的解题能力,促进创造性思维的培养.

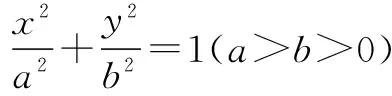
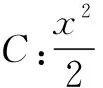
由此可见，类比在求解问题中有着广泛的应用.在解题教学中通过类比,授之以法,并进行有效的训练,引导学生推广数学命题;或通过类比,探求解题途径,可以达到梳理知识,归纳题型,总结解题方法的作用,能够深化学生对知识的理解,深化学生对数学思想方法的掌握.通过类比,拓展学生的数学能力,这样做既有利于学生记忆和掌握所学知识,又有利于培养学生思维的灵活性，提高学生的发现问题、分析问题和解决问题的能力,提高学生的实践能力和创新精神．

四、在习题课教学中运用类比,促进类比思维能力的提高

类比推理是各种逻辑思维方法中最富于创造性的一种方法,它可以跨越各类事物的界限,进行不同事物间的类比,既可以比较事物的非本质属性(如形式和研究方法),又可以比较事物的本质属性．所以，在新课程背景下,教会学生应用类比的思想对数学问题进行分析、理解,以及最终解决问题是高中数学教学的重要内容．特别是在习题课与讲评课的教学中,引导学生学会类比思想,研究不同知识之间的联系,通过联想的方法对新旧知识进行比较,从而找到解决问题的手段与方法．

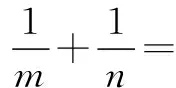
通过观察，可以发现此三道题所求结论的结构形式完全相同,不同的就是已知条件的背景不相同,分别以抛物线、椭圆、双曲线为背景,在类比探究中可以寻求到处理圆锥曲线焦半径问题的一类通法．

五、应用类比要注意的两点问题

(1)类比时一定要找准类比对象,防止类比的陷阱和形式上的类比,绝不能为了类比而类比.在运用类比方法得出结论的过程中,有可能学生所得到的结论不能直接用于原来的问题,这个时候,教师就要启发或帮助学生重新考虑问题的解答,适当修改甚至变更策略,直到尝试过解答的各种形式以后,找到一个可拓展到原来的问题为止．

(2)要克服一些错误的类比,如易混概念的类比,以及易混性质的类比,从而准确地掌握概念和性质的本质,有区别地认识具有某种相似性的概念．

法国数学家拉普拉斯曾说过:“甚至在数学里,发现真理的主要工具也是归纳和类比．” 根据高中生的抽象逻辑思维从经验型向理论型急剧转化的心理特点和高中数学教材的特点,教学中恰当地应用类比方法,不仅能突出问题的本质,提高教学质量,而且有助于培养学生的创造能力等思维品质,提高认识问题和解决问题的能力．