探究问题串设计的四个度

史玉花

(江苏省苏州工业园区第二高级中学，215121)



探究问题串设计的四个度

史玉花

(江苏省苏州工业园区第二高级中学，215121)

伽利略说过:“数学是科学的大门和钥匙.”而打开数学之门的无疑是问题.可见,问题在整个科学研究中的重要性,没有问题的不断出现,我们的科学将停滞不前.同样,在我们的教学设计中,设计什么问题、怎样设计问题关乎到整个课堂的教学效果.所以，我们教师要根据教材内容的重点和难点认真挖掘其深度和广度,高屋建瓴,精心设计有核心度、有梯度、有发散度和创新度的问题串,真正体现“问”的魅力和艺术,激发学生的学习热情,提高教学效率.本文从以下四个方面切入,论述问题串设计的四个度.

一、问题串的设计要围绕一个核心,即要有核心度

教育心理学认为教学目标是预期学生通过教学活动获得的学习结果.每节课都有教学目标,所以，在教学设计时,所有问题都应该围绕这一核心目标展开,通过一系列的问题研究,引导学生不断地深入思考,最终达成教学目标.以下是等差数列求和公式的探求教学案例中的问题串:

问题1等差数列中有哪些基本量?

问题2等差数列有什么性质?

问题3就书本上的问题:某仓库堆放一堆钢管,最上面的一层4根,下面的每一层都要比上一层多一根,最下面的一层有9根,怎样计算这堆钢管的总数呢?你有什么好的办法计算4+5+6+7+8+9?

问题4那么对于一般的等差数列{an},其前n项和Sn=a1+a2+…+an=?(用基本量表示)

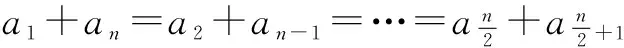
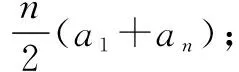
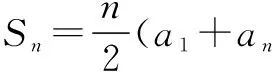
教师可以利用4+9的实际意义加以引导,即在4根钢管基础上再加上9根钢管(如图1).

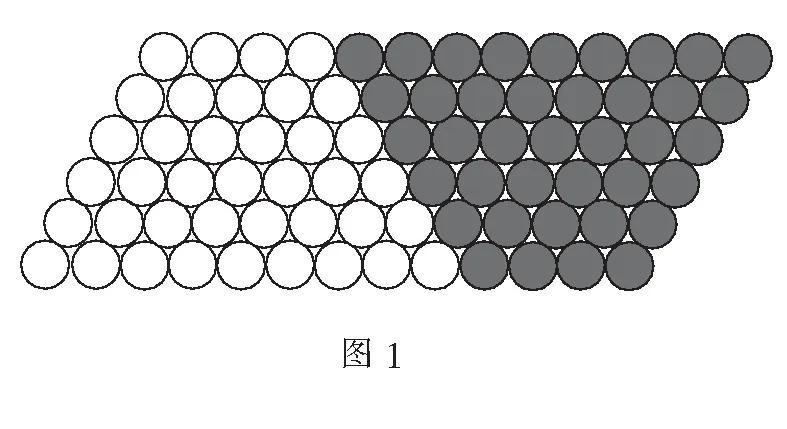
从视觉上感知原来的一堆钢管被倒序堆放,并与前一堆钢管合并即求和,那么学生就很容易从图中看出原钢管总数

预设2通过钢管求和的作图演示,得Sn=a1+a2+…+an，又Sn=an+an-1+…+a1,再把两式相加(即上述的倒序相加),利用等差数列的性质，得

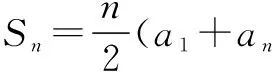
以上4个问题都是为了探求等差数列求和公式这一目标而一一展开.以回顾基本量及性质为铺垫,结合实际问题引出数学问题,利用性质解决问题,锻炼学生的抽象思维及转化问题的能力,体会由特殊到一般的研究方法.

二、根据问题的深度适度加密,体现问题串的梯度

《学记》曰:“善问者如攻坚木,先其易者,而后其目.”也就是说,善于提问的教师应该由易到难、由繁至简地设计问题串,层层推进,使学生不断地深入下去,逐步达成问题的解决.这就要求教师有必要把一个难题分解成几个小题,给学生一些台阶,这也符合最近发展区理论及认知规律,让学生不断地在小题的解决中增强自信,激发学生对后续问题研究的热情.以下是笔者在“函数中的分类讨论思想”高三复习课上的教学设计片断中的问题串:

问题1先求解下述基础题:

(1)求函数f(x)=2x2-ax-1 (a∈R)在[0,1]上的最小值;

(2)求函数f(x)=x2-2x-1在[t,t+1]上的最小值;

(3)求函数f(x)=x|2x-a|(a∈R)的单调区间.

问题2求函数f(x)=x2-ax-lnx(a∈R)的单调区间.

问题3讨论函数f(x)=x2-ax-lnx(a>0)在[a,+∞)上的单调性.

问题4讨论函数f(x)=x|x-a|-lnx(a∈R)的单调性.

问题4若直接让学生入手,讨论情况复杂,很多学生望而却步.笔者把这一大题适当加密,先通过问题1的三个小题让学生热身,进入分类讨论的情境.问题2是研究复杂函数的单调性,利用导数立即就转变成了一个二次含参函数y=2x2-ax-1在(0,+∞)上符号的研究.问题3改变了问题2中的参数范围及定义域,正是定义域的变化导致需要对方程2x2-ax-1=0的大根与参数a的大小讨论.由问题2的铺垫,问题3的解决就显得自然顺畅了.最后再看问题4,由热身练习知先去绝对值,当然此时需要对参数a与0的大小进行讨论:

若a≤0,则f(x)=x2-ax-lnx的单调区间就同问题2;

若a>0, 则

先看x≥a时,f1(x)=x2-ax-lnx(a>0)的单调性就是问题3；再研究最后一种情况:x0)的单调性(过程略).前面3个问题都是为问题4服务的,而且这四个问题是层层递进,由易到难,符合学生的认知规律,使不同层次的学生都能有所收获,充分体现了教学设计中问题串设计的梯度性.

三、根据问题的可扩性,横纵双向发展,体现问题串的发散度

这里所谓的发散度就是由一个问题出发,可以联想到哪些与之相关的问题.通过这一系列相关问题串的研究,将问题研究得更透彻,理解得更深入,让学生体会到玩数学的趣味性.下面是笔者“关于不等式的综合应用”复习课的教学中的问题串:

问题1设不等式x2-2ax+a+2≤0的解集为M,如果M⊆[1,4],求实数a的取值范围.

问题2设不等式x2-2ax+a+2≤0的解集为M,如果[1,4]⊆M,求实数a的取值范围.

问题3设不等式x2-2ax+a+2≤0的解集为M,记N=[1,4],若M∩N≠∅,求实数a的取值范围.

问题4若∀a∈[-2,-1],不等式x2-2ax+a+2≤0恒成立,求实数x的取值范围.

问题5若∃a∈[-2,-1],使不等式x2-2ax+a+2≤0成立,求实数x的取值范围.

问题2、3是在问题1的基础上根据集合的有关概念,改变条件,就改变了二次函数图象和区间[1,4]的关系,导致参数范围不同.问题4、5是将前三个问题中的参数与变量互换及改变量词而产生的.这一系列发散性的问题串可帮助学生深切体会二次函数图象在研究一元二次不等式中的重要性,也帮助学生更深刻地理解变量与参数的辩证关系.

四、根据问题的本质,大胆类比猜想,体现问题串的创新度

牛顿说过:“没有大胆的猜想就做不出伟大的发现.”类比猜想是根据两个或两类对象之间在某些方面的相似或相同,从而猜测它们在其它方面也可能相似或相同的一种猜想.在数学研究中,类比猜想是一种发现问题、解决问题的好方法.在教学中,通过问题串,引导学生大胆地去猜想,发现问题,再想办法论证问题的正确性或举出反例否定猜想,从而促使学生从“学会”到“会学”的转变,提高学生的提问及创新能力.例如下面两个教学案例中的问题串：

教学案例1

问题1O是坐标原点,在圆O中,AB是圆O的直径,C是圆O上异于A、B的任意一点,若直线AC和直线BC的斜率存在,则kAC·kBC=?类比猜想到其他高中所学的圆锥曲线中能有什么样的结论?并可以证明吗?

问题2在椭圆M中,A、B为长轴的端点,C是椭圆M上异于A、B的任意一点,则kAC·kBC=?能证明吗?

问题3在双曲线M中,A、B为实轴的端点,C是双曲线M上异于A、B的任意一点,则kAC·kBC=?能证明吗?

教学案例2

问题1过抛物线y2=2px(p>0)的焦点F作一条直线与抛物线交于A、B两点,过A、B分别作抛物线y2=2px的切线PA、PB,则交点P在抛物线y2=2px的准线上.能证明此结论吗?能推广到其他圆锥曲线上得到类似的结论吗?

问题2在椭圆M中,过其右焦点作直线交椭圆于A、B两点(异于椭圆与长轴的交点),过A、B分别作椭圆的切线PA、PB,则交点P一定在椭圆的右准线上.能证明此结论吗?

问题3在双曲线M上,过其右焦点作直线交双曲线于A、B两点(异于双曲线与实轴的交点),过A、B分别作双曲线的切线PA、PB,则交点P一定在双曲线的右准线上. 能证明此结论吗?

问题串设计的好坏直接影响课堂教学效果.我们作为教师,就应该在问题串的设计上多下功夫,认真研究问什么、怎么问、什么时候问等问题.以上是笔者关于问题串设计的四个度,不尽完善,给大家一些参考,让我们设计出更加适合学生的教案,高质量地完成知识的传递、方法的传授及能力的提升！