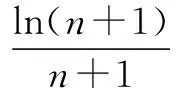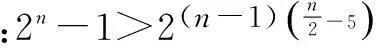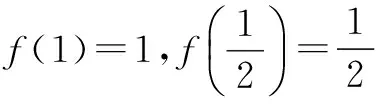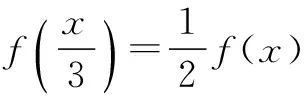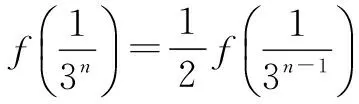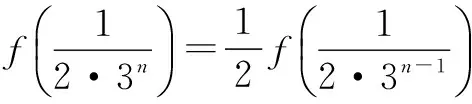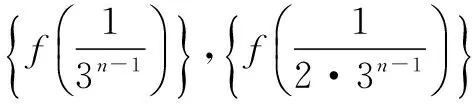与正整数相关问题解法探析
周丽娜
(江苏省昆山中学,215300)
○解题研究○
与正整数相关问题解法探析
周丽娜
(江苏省昆山中学,215300)
对于与正整数n有关的数学命题,现行教科书(苏教版)仅在《选修2-2》“数学归纳法”一节中有论述,除此再无系统提及.但此类问题,以各种形式散见于包括高考在内的各种考试卷中,不少学生往往找不到合理的解题切入点而束手无策.本文对此类问题的常见解法作些探求,以希指正.
一、充分利用正整数的性质
现代数学中正整数是通过皮亚诺公理对其进行了刻画和约定的,由此可以推出关于正整数的各种性质.
比如:离散不等式(若x,n∈N*,则x>n等价于x≥n+1);正整数的唯一分解定理(算术基本定理)等.
讨论与正整数相关问题时自然要充分利用相关性质.
1.离散性
与实数的连续性相比,正整数集是离散的,相邻两正整数之间是有间隙的,解题时若能充分注意这种区别往往事半功倍.
例1已知an=n2+λn(n∈N*),若数列{an}单调递增,则实数λ的范围是______.
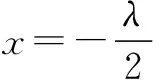
例2已知bn=an+1(n∈N*),若|bn|≥|b5|对正整数n恒成立,则实数a的取值范围是______.

2.可数性
在某有限范围内的正整数只有有限多个,满足某种特定关系的正整数是可数的.因而,解题时,确定目标量的范围或所满足的特定关系是解题的关键.

(1)求an及Tn的表达式;
(2)是否存在正整数m,n(1 (2)假设存在m,n∈N*且1 ① 解得 ② ∵n∈N*,则-2m2+4m+1>0, ∴m=1或m=2. ∵m>1,∴m=2代入②,得n=12. ∴存在正整数m=2,n=12满足题意. 评注以上解答中,面对①,一个等式中有两个未知量,学生往往无所适从,是教学的一个难点. (1)试写出{an}的一个3项子列,并使其为等差数列; (2)若{bn}是{an}的一个m(m≥3)项子列,且{bn}为等比数列,求证: ∴b1+b2+…+bm ∴b1+b2+…+bm =b1(1+q+q2+…+qm-1) 3.可分类性 正整数n与其它实数一样可进行合理分类,常见的可分成奇数和偶数两大类. (1)求{an}的通项公式; (2)当λ=4时,是否存在互不相等的正整数r,s,t,使ar,as,at成等比数列?若存在,给出r,s,t满足的条件,若不存在,说明理由. 解(1)an=(2n+1)λn-1.(过程略) (2)当λ=4时,an=(2n+1)4n-1. 刘佳走的时候,我去送他,他把领结摘了,要拿它换被我硬抢走的乳牙,我却把领结一并抢了过来,歪里歪气地说,这玩意儿跟上吊一样样的。 (2s+1)242(s-1)=(2r+1)(2t+1)4r+t-2, 两边同除以4r+t-2,得 (2s+1)242s-(r+t)=(2r+1)(2t+1). 根据等式两边的奇偶性,知 也即2s+1=2r+1=2t+1,s=t=r,矛盾. 故这样的r,s,t不存在. 此外,对含有(-1)n(n∈N*)的问题,解题中常需要根据n的奇偶性进行分类讨论,这里不再赘述. 正整数n也是实数,因而,有些问题的讨论可以在实数(更广的)范围研究,再将正整数n作为特殊的实数看待,使解题收到奇效. 例6(教科书(苏教版)高中数学选修2-2)试比较(n+1)n与nn+1(n∈N*)的大小. 又依题意:当0≤x1≤x2≤1时, f(x1)≤f(x2), 总之,在中学数学中,与正整数n有关的问题,题材丰富,题型活泼多变,解题方法灵活多样,深受中学生喜爱.笔者以为,在实际教学中,从正整数自身的特性出发去研究问题、解决问题,往往能抓住问题的本质,找准解决问题的切入点.对学生,无论从应对高考,还是从培养其良好的思维品质,提高其数学素养,都将起到积极的建设性作用.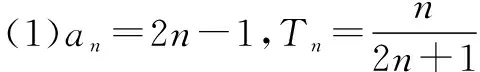
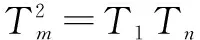

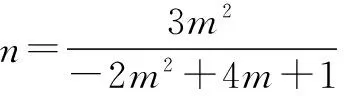

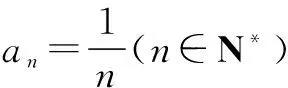
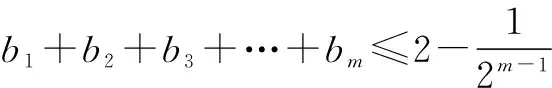
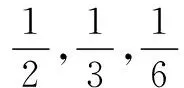
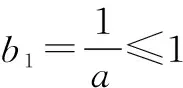
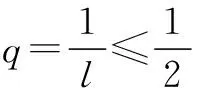
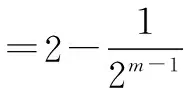

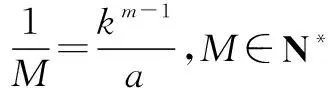

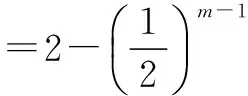
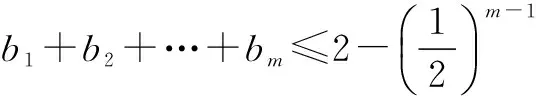
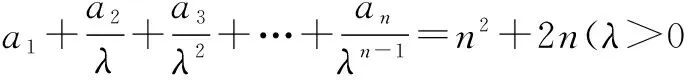
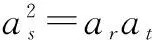
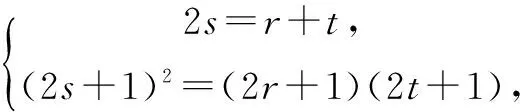
二、充分利用正整数为实数的性质