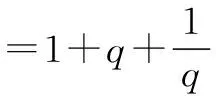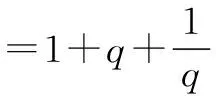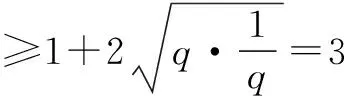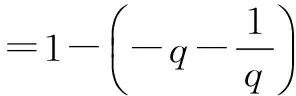高三二轮复习中数学思想方法的渗透
马恩云
(云南民族大学附属中学,650000)
高三二轮复习中数学思想方法的渗透
马恩云
(云南民族大学附属中学,650000)
在高考数学命题者眼里,数学的本质不是孤立的问题与解法,而是一整套知识理论体系与思想方法.高考一轮复习是构建知识网络的整套理论体系,而在二轮复习中应以思想方法为核心,使学生在归纳整理及提炼的过程中,体会蕴含在其中的思想方法.高考二轮复习阶段是高三下学期教与学承上启下的时期,是促进知识灵活运用、提高能力的重要时期,是发展学生思维水平、促进学生大幅度提升能力的关键时期.关注数学思想方法的归纳整理,是优化学生思考问题、解决问题的思维策略、提升能力水平的有效途径之一.本文就中学数学中的函数与方程的思想、转化与化归的思想、数形结合的思想、分类讨论思想、特殊与一般的思想在高考二轮复习中的地位和导向作用,分类举例说明,以期更好地做好高考二轮复习.
一、函数与方程的思想
函数思想,是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图象和性质去分析问题、转化问题,从而使问题获得解决.函数思想是对函数概念的本质认识,用于指导解题时就是要善于利用函数知识或函数观点观察、分析和解决问题.方程的思想是对方程概念的本质认识,用于指导解题时就是要善于利用方程或方程组的观点观察处理问题,即分析数学问题中变量间的等量关系,建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决.
例1设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出S1、S2、S3…,S12中哪一个最大,并说明理由.
解(1)由a3=12,得a1=12-2d.
∵S12=12a1+66d=144+42d>0,
S13=13a1+78d=156+52d<0,
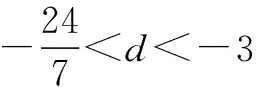
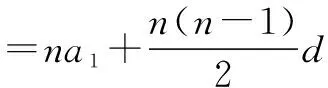
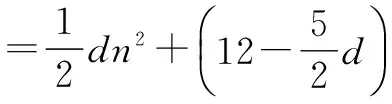
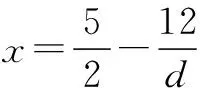
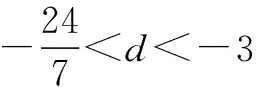
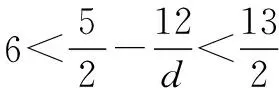
∴当n=6时,Sn最大.
反思数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列中的最值问题显得十分重要.
二、转化与化归的思想
转化与化归思想是指把待解决的问题通过转化归结为在已有范围内可解的问题的一种思维方式.具体地讲,转化思想方法是实现问题的规范化、模式化,以便应用已知的理论、方法和技巧,达到使问题解决的目的.化归思想方法是在研究和解决有关数学问题时,采用某种手段和方法将问题通过变换使之转化,进而使问题得以解决的一种方法.
例2(2014年四川高考题)设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|+|PB|的取值范围是()
解析由题意可知,定点为A(0,0),B(1,3),且两条直线互相垂直,其交点P(x,y)落在以AB为直径的圆周上,所以
|PA|2+|PB|2=|AB|2=10,

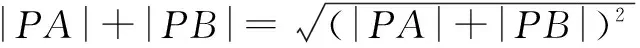


故选B.
反思转化和化归的思想方法,在运用时应注意用“变换”的方法解决数学问题,依据问题本身提供的信息,去寻求有利于解决问题的变换途径和方法,进行合理的选择.
三、数形结合思想
华罗庚先生曾对数形结合的思想和方法赋诗:“数与形,本是相倚依,焉能分作两边飞;数缺形时少直觉,形少数时难入微;数形结合百般好,隔离分家万事休;切莫忘,几何代数流一体,永远联系莫分离.”数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题能迎刃而解,且解法简捷.所谓数形结合,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法.数形结合思想通过“以形助数,以数解形”,使复杂问题简单化、直观化,抽象问题具体化,能够变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性与灵活性的有机结合.

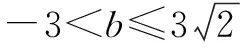
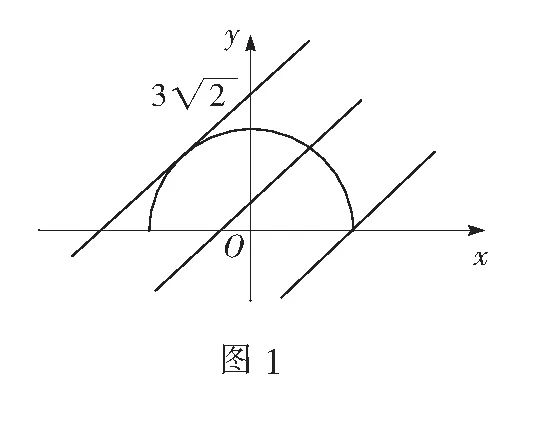
反思运用数形结合解决最值问题,关键是在直角坐标系中作出方程所表示的曲线,再将所求最值转化为直线在y轴上的截距,结合图形可解.
四、分类讨论思想
分类与讨论思想是一种重要的数学思想方法,该思想方法的基本思路是将一个较复杂的数学问题分解(或分割)成若干个基础性子问题,通过对基础性子问题的解答来实现原问题的解决.对问题实行分类,其分类标准等于增加了一个已知条件,实现了有效增设,将大问题(或综合性问题)分解成小问题(或基础性子问题),优化了解题思路,降低了问题难度.
例4已知函数f(x)=logax在[2,π]上的最大值比最小值大1,则a等于()

分析研究函数的最值需考察函数的单调性,而题中对数函数的增减性与底数a的取值有关,故应对a进行分类讨论.
解(1) 当a>1时,f(x) 在[2,π]上是增函数,最大值是f(π),最小值是f(2),据题意,有
f(π)-f(2)=1.
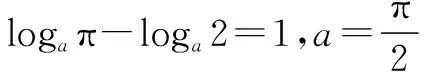
(2) 当0 f(2)-f(π)=1 由(1) (2) 知,故选C. 反思题中字母a的取值范围的不同,直接影响了函数的性质,从而导致了两种不同的情形,所以必须对字母a进行分类讨论.对分类问题的求解歩骤:一是确定分类的对象,即对哪个变量或参数进行分类;二是合理分类,即对所讨论的对象进行合理的分类;三是逐类讨论,即对各类问题详细讨论,逐步解决;四是归纳总结,即将各类情况汇总,写出结论. 由特殊到一般再由一般到特殊反复认识的过程是人们认识世界的基本过程之一,数学研究也不例外.这种由特殊到一般,由一般到特殊的研究数学问题的基本认识过程就是数学研究中特殊与一般的思想.特殊与一般的思想既指出了数学的思维方向,又给出了有效的解题策略. 例5(2008年四川高考题)已知等比数列{an}中a2=1,则其前3项的和S3的取值范围是() (A)(-∞,-1] (B)(-∞,0)∪(1,+∞) (C)[3,+∞) (D)(-∞,-1]∪[3,+∞) 分析本题中的等比数列只知道a2=1,如果再知道公比,数列就可以确定,而选项是范围问题,可取定公比加以排除. 解法1因为等比数列{an}中a2=1,所以当公比为1时,a1=a2=a3=1,S3=3.当公比为-1时,a1=-1,a2=1,a3=-1,S3=-1,从而淘汰A,B,C.故选D. 解法2等比数列{an}中a2=1, ∴S3=a1+a2+a3 当公比q>0时, 当公比q<0时, ∴S3∈(-∞,-1]∪[3,+∞),故选D. 反思取特殊数列入手淘汰,如果一次不能区分,则需多次取有区分度的值进行排除,直至能辨别出正确答案为止,也可多种方法并用.不具备就要进行分类讨论.相比之下,取特值的方法优于通性通法.特殊与一般的思想方法是广泛适用的一种重要的数学思想方法,对于一般性问题、抽象问题、运动变化问题和不确定问题都可考虑运用特殊与一般的思想方法去探求解题途径.对于递推数列问题,采用“归纳——猜想——证明”的方法去解决问题,首先通过特例探索、发现一般规律,然后再用这个规律来解决其他特殊问题,这是特殊与一般思想最常见的应用之一. 对于某些特殊的问题,如求值、比较大小等,要注意研究其数量特征,发现一般模型,再由一般解决特殊. 总之,数学思想方法是对数学规律的理性认识,数学学习在于掌握书本知识,更在于养成良好的数学思维习惯.高考二轮复习过程中教师应在教学的每一个环节中重视数学思想方法的渗透,使学生对数学知识和所使用的方法有本质的认识,从而提高学生的解题能力.这样做就能有效避免复习备考的盲目性和随意性,在有限的备考时间内让复习效率最大化.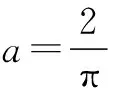
五、特殊与一般的思想