一道课后习题的错因探究及教学思考
章东锋
(江苏省锡山高级中学,214174)
一道课后习题的错因探究及教学思考
章东锋
(江苏省锡山高级中学,214174)
《普通高中课程标准实验教科书·数学(选修2-2)》(苏教版)第1章“导数及其应用”在整个高中教材中的地位和作用是非常重要的,它既是对函数知识的补充和完善,也为今后学生进入大学学习微积分奠定基础.纵观2010年到2015年这6年的江苏高考试卷,导数试题很受命题者的青睐.从试题的分布看,其中2年放在第20题,3年放在第19题,1年放在第18题,由此可见导数与函数、不等式的综合应用问题地位之重要.本文以笔者在课后作业批改中遇到的一道导数应用问题为例谈谈自己对于导数及其应用这类问题的教学思考.
一、样题呈现
设函数f(x)=x4+ax3+2x2+b(x∈R),其中a,b∈R.
(1)若函数f(x)仅在x=0处有极值,求a的取值范围;
(2)若对于任意的a∈[-2,2],不等式f(x)≤1在[-1,1]上恒成立,求b的取值范围.
二、问题再现
笔者任教高二两个理科班,学生基础都比较好,然而从该题的批改及统计情况看,学生的错误率非常高,对错因的探究引起了笔者的兴趣.
由于样题中第(1)问的解答正确与否直接影响第(2)问的解答,故以下主要探究样题中第(1)问的解题思路.
学生思路:
f′(x)=4x3+3ax2+4x.
由于f′(x)为三次函数,故再次求导,得
f″(x)=12x2+6ax+4.
考查方程f″(x)=0.
∵函数f(x)仅在x=0处有极值,
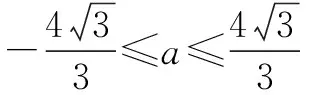
此时f″(x)≥0恒成立,∴f′(x)在(-∞,+∞)上单调递增.又f′(0)=0,∴f′(x)在(-∞,0)上恒小于0,在(0,+∞)上恒大于0(如图1),即y=f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.又f(0)=b,∴y=f(x)仅在x=0处取得极小值f(0)=b(如图2),∴a的取值范围为
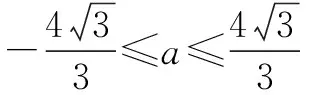
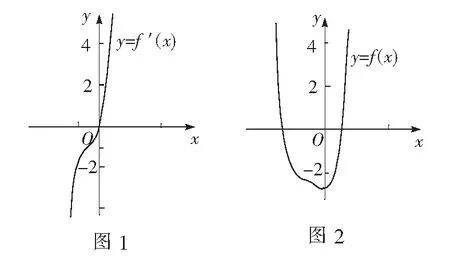
初看学生解答过程,抓住原函数的单调性与其导函数的符号关系,通过两次求导,利用数形结合思想求出参数a的取值范围,可谓思路清晰,解答完整,毫无破绽.
三、问题详探
在讲评样题时,笔者将正确解答呈现给学生,通过两种解答的对比让学生找寻自身解答错误的根源所在.
正确解答如下:
f′(x)=4x3+3ax2+4x
=x(4x2+3ax+4).
∵x=0不是方程4x2+3ax+4=0的根,若要使函数f(x)仅在x=0处有极值(如图2),则必须使4x2+3ax+4≥0恒成立,即
Δ1=9a2-64≤0,
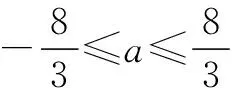
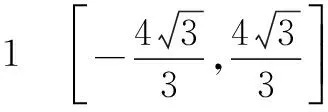
f′(x)=4x3+8x2+4x
=4x(x2+2x+1)
=4x(x+1)2.
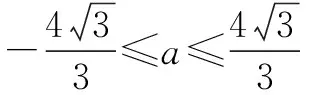
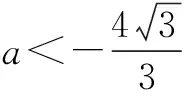
生2:此时不妨记f″(x)=0的两根为x1、x2(x1 问题3能否找到符合上述条件的函数y=f′(x)使得函数y=f(x)仅在x=0处有极值? 生3:若要使y=f(x)仅在x=0处取得极值,则可构造f′(x)的图象(如图4).即y=f′(x)在(-∞,0)上恒小于等于0,在(0,+∞)上恒大于等于0,∴4x2+3ax+4≥0在R上恒成立,即Δ1=9a2-64≤0,解得 从题目解答的分歧处设计问题,层层深入,逐步探究,将学生的思路引向问题解决的方向,通过学生自主构造符合条件的函数y=f′(x),使问题得以解决. 1.热点考点重笔墨 以函数为载体,导数为工具,在函数与导数的交汇处命题,是导数进入高中数学后的一个热点考点,常考常新.从近6年的江苏高考题可以看出考查的函数主要以含参的三次多项式函数及与指数函数y=ex或对数函数y=lnx相关的函数为主,重点研究函数的单调性、值域、极值等性质.因此,针对导数教学而言,教师必须把教学的重点放在与这几种初等函数相关的函数的性质的研究上,尽量避免在繁、难、偏、怪的函数题型上花时间. 2.数学思想重渗透 导数及其应用的灵魂是数学思想.在重视基本概念和基本方法的基础上,体悟有关的数学思想显得尤为重要.在导数和积分的问题中常见数学思想主要是数形结合思想、分类讨论思想、函数方程思想、转化化归思想.同一个数学问题,由于思考的角度不同,对问题的分析、理解的层次不同,导致目标转化和方法的不同.如样题中对于函数y=f′(x)是分解因式还是再次求导,通过对比体悟,从简单、显性、具体着手,很快地解决问题,这有助于培养学生解决问题的能力,渗透转化化归思想,优化思维品质.在导数的应用中,分析原函数和导函数的图象,能够解决许多重要的问题.在上文中问题1、2、3解答结束后,我们还可以利用几何画板软件画出f″(x)的图象,通过有向线段AB的数量来控制a的值的变化,在图形的运动变化中让学生更全面、清晰地理解y=f(x)、y=f′(x)与y=f″(x)三个图象之间的关系,渗透数形结合思想. 3.学生活动重思维 4.教师教学重实效 数学课的课型一般分为:新授课、讲评课、复习课等.在实际教学中我们经常会有这样的体会:在讲评课和复习课上,虽然教师很卖力地讲解,但是学生并没有报以相应的热情,这样直接导致教学任务的搁浅和教学效率的降低.布鲁纳认为:“探索是数学教学的生命”,在课堂上我们可以尝试在这些课型中多一点探究和互动环节.如本文中问题详探环节,在给出正确解答后并没有就此搁笔,而是通过3个问题的设置,层层深入,在探究和师生互动中将问题顺利解决.作为一线教师,在平时的教学过程中,我们经常会碰到一些有关导数及其应用问题的好题,我们除了要研究清楚题目的正确解答以外,还要充分挖掘其内在的本质.如为什么错?怎样纠正?是否有更好的解决方案?该问题是否可以拓展延伸?通过归纳整理,有效整合,将它们应用到我们的课堂教学中,避免出现为讲评而讲评、要探究才探究的现象,真正将课堂教学落到实处.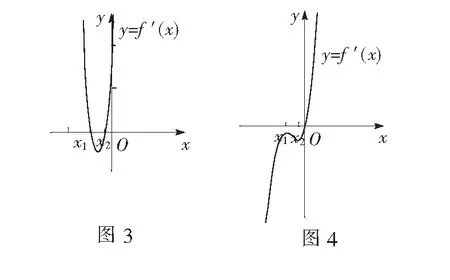

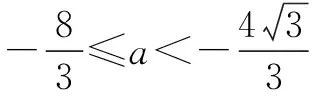
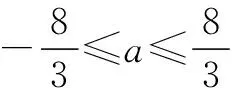
四、教学思考