“同角三角函数的基本关系”教学设计

刘汉军

(陕西省延安市志丹县高级中学,717500)



“同角三角函数的基本关系”教学设计

刘汉军

(陕西省延安市志丹县高级中学,717500)

一、教材分析

1.教材的地位和作用

同角三角函数的基本关系是普通高中课程标准实验教科书(北师大版)数学必修4第三章三角恒等变形的内容．三角函数是高考的重要内容,本节内容是整个三角函数知识的基础,也是三角恒等变形的关键,与第一章中任意角的三角函数关系非常密切,在教材中起承上启下的作用；同时,本节课体现的数学思想与方法在整个高中数学学习中有重要作用．

2.教学目标

(1)知识与技能.掌握同角三角函数的基本关系式、变式及其推导方法;会用同角三角函数的基本关系式及变式求值化简．

(2)过程与方法.在掌握同角三角函数的基本关系式的基础上,能灵活运用于解题,提高学生分析、解决三角问题的能力,培养学生观察发现能力,增强数形结合的思想．

(3)情感、态度与价值观.让学生亲身经历数学研究的过程,体验探索的乐趣,进一步培养良好的思维习惯．在问题提出和解决的过程中,培养学生主动探究知识、合作交流的意识;通过小组讨论活动,培养学生团队合作意识．

3.教学重点与难点

(1)重点:同角三角函数的基本关系式推导及应用；

(2)难点:同角三角函数的基本关系式及变式的灵活运用.

二、教法学法分析

(1)教法:自主学习+合作探究+交流展示.

(2)学法:着重体现学生主体地位,以学生自主探究为主,让学生变被动接受知识为主动索取知识;通过观察、猜想、分析、归纳来推导新知识,让学生积极参与到课堂教学中,体验成功的喜悦．

三、教学过程设计

1.复习导入

(1)任意角的三角函数概念；

(2)正弦函数、余弦函数及正切函数在各象限的符号.

设计意图三角函数的概念是推导证明同角三角函数基本关系的关键,三角函数在各象限的符号是关系式应用的基础．

2.自主学习

(1)填空

sin 30°=______；cos 30°=______；

sin230°+cos230°=______；

tan 30°=______；

sin 0°=______；cos 0°=______；

sin20°+cos20°=______；

tan 0°=______；

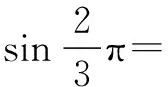
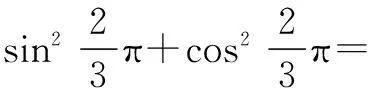
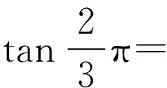
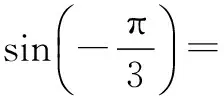
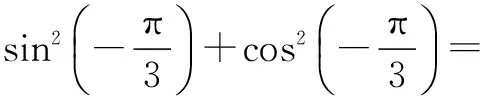
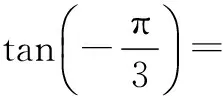
(2)根据上面问题的解答你发现了什么规律?你能用代数式表示这个规律吗?你能证明自己得到的结论吗?

师生活动:自主学习内容由学生课前预习课本,思考完成．课堂上教师检查学生完成情况,提问学生回答设置的问题．小组交流时由学生给出发现的规律,得出同角三角函数的基本关系式并证明．解读关系式中“同角”的理解及商数关系中应注意的条件．教师板书同角三角函数的基本关系式:

平方关系:sin2α+cos2α=1：

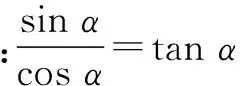
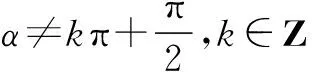
设计意图新课标强调学生的观察、思考、探索、推理,本题组通过设置问题串,层层递进,使学生经历根据特例进行归纳、建立猜想、用数学符号表示、并给出证明这一重要的数学探索过程．

3.合作探究

(根据本题的解答,课后自主解决课本例3)

师生活动:小组合作讨论,教师巡视指导,对有困难的小组加以帮助.学生展示交流成果(分小组学生上黑板讲解,有疑问的学生可以提问)；教师点评激励并强调解题书写的规范性．通过合作探究三道题,重在掌握三个三角函数中,知一会求其二,并体会分类讨论思想的应用．

设计意图合作探究通过学生先思考,然后小组讨论,教师通过巡视,对有困难的学生加以指导．经过学生合作讨论,亲自体验解题思路的形成过程,学会分析问题、解决问题的方法,培养学生分类讨论的思想,突破本节基本关系式应用这一重难点．选择一道同类型的高考真题,进一步激发学生学习的欲望．

探究2已知tanα=-3,求下列式子的值：

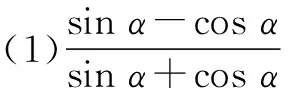
式中:σs为发射截面,N1和N2分别受激辐射过程中低能态和高能态上的粒子数密度。将式(1.2)代入式(1.1),阈值条件变为

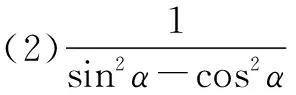
师生活动:小组合作讨论,教师巡视指导,引导学生多角度思考问题(由正切求出正余弦;条件切化弦;所求式子弦化切).学生展示交流成果(按三种思路有针对性地叫三名学生展示),教师点评激励．

设计意图弦切互化是解决三角函数问题的重要思路．本题通过一题多思、一题多解、一题多讲,既开阔了学生的视野,又训练了学生的思维,更展示了学生的能力.从三种解法的求解过程中让学生在无穷的变换中领略数学的魅力,体会数学学习的乐趣,激发数学学习的兴趣．

4.练习巩固

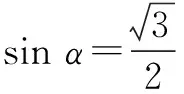
(3)已知tanα=2,求下列式子的值：

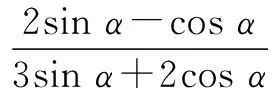
师生活动:学生独立解答后,小组回答解题结果,教师点评．

设计意图一个新知识的出现,要达到熟练运用的效果,仅仅了解是不够的,一定量的“重复”是有效的,也是必要的,这就是所谓的“温故而知新”、“熟才能生巧”．通过三道练习进一步强化学生对本节核心知识的掌握．

5.小结

教师引导学生从以下三方面自主小结:

(1) 本节课学习了哪些同角三角函数的基本关系式?每个关系式成立的条件是什么?

(2) 本节课的学习主要解决了什么问题?根据一个三角函数值求另外两个值时的难点是什么?如何突破难点?

(3) 本节课体现了哪些数学思想方法?你还有什么疑问吗?

设计意图课堂小结是课堂教学的最后一个环节.教师或学生根据本节课的内容有针对性地从知识和方法的角度进行归纳总结,可以起到加深巩固的作用,进一步强化了学生对知识的记忆和掌握,达成学生对知识的自我发现、自我生成、自我应用、自我完善，让学生获得了成就感．