谈“数学归纳法”的教学设计

肖　辉

(江苏省南京市第十三中学，210008)



○教学研究○

谈“数学归纳法”的教学设计

肖辉

(江苏省南京市第十三中学，210008)

前苏联著名数学教育家A.A.斯托利亚尔曾说过:“数学教学可以表示一种思维活动,或者表示这种活动的结果——理论．”数学从微观上看是一种思维活动,数学教育是思维的教育;从宏观上看,又是一种文化,一种观念系统,数学教育是数学文化的教育．

本节课的教学内容“数学归纳法”是典型的三段论,看似简单而机械,学生掌握其证明步骤不难,靠模仿就可以习得,但其中蕴含的重要的数学思想和极大的数学价值,是不容易感悟的．如果我们在教学中只是对其进行演绎推理般的应用,那就放弃了一次让学生真正体验“数学化” 思想的历程,抛弃这节课的精华与灵魂,学生也就失去了一次数学理性思维提升的过程．

在本课例的设计中,笔者用一条主线将三个教学内容按逻辑顺序串联起来:用数学的眼光来看世界→用数学的语言来描述世界→用数学的方法来研究世界．这条主线是我们这节课的教学顺序,以此推动学生思维的发展,从本质上来说也是我们“学数学”和“用数学”的基本环节,学生在这个过程中可以接受到数学文化的熏陶．

下面是本节课的教学设计过程:

一、问题提出

新教材强调数学理论形成的背景,重视介绍数学知识发生发展的来龙去脉,注重帮助学生学会运用数学语言去描述周围世界出现的数学现象,注重帮助学生体验数学在解决实际问题中的作用,拓展学生的视野,从而体会数学的应用价值．我们更希望学生能在解决实际问题中,感悟数学的作用,体验数学与日常生活及其他学科的联系,逐步形成和发展数学应用意识,提高实践能力．

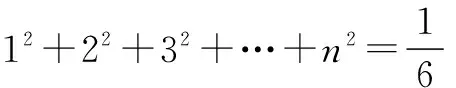
问题1上述数学问题你打算怎样解决?

设计意图课堂的开始播放三段视频,从生活问题引入,让学生感知生活中有很多类似的问题．同时为学生营造轻松、愉快的学习氛围．在每段视频播放的过程中,适当引导学生关注每个问题涉及的有关对象，紧接着提出一个数学问题．这里仅需要学生想到取几个特殊的n值,从中寻找规律即可(基于特例的不完全归纳法)．

问题2将三个生活中的问题和一个数学问题放在一起，上述问题有何共同点?(从生活中举例)

共同点:① 很多个,无限项;② 用正整数计数,与正整数有关;③ 传递.

(生活实例:① 放鞭炮,② 早操排队对齐)

设计意图将生活中的问题和数学问题放在一起,找共同点,旨在为寻找解决问题的方法做铺垫．让学生举生活中的例子,旨在让学生感知生活中有很多类似的问题，问题源于生活．

二、用数学眼光看问题

我国著名的数学教育家张孝达先生曾经说过这样一句话:“祝愿我们数学教育工作者做出无愧于时代的贡献,给我们所有的学生一双能用数学视角观察世界的眼睛,一个能用数学思维思考世界的头脑,一副为谋国家富强人民幸福的心肠．”

“一百个人的眼中,就有一百个哈姆雷特”.我们作为数学教育者有责任培养学生从现实世界中寻找“数学”的眼光与能力．

问题3生活中有这样一类问题,它有无限项,且无限传递．对于这类问题,生活中是怎样解决的呢?以多米诺骨牌为例,怎样才能使所有骨牌全部倒下?

问题4再以烽火台传信为例,怎样才能使信息传布出去?

设计意图以两个典型的生活问题,让学生描述问题解决的要领．让学生充分感知,并适当提炼:① 第一块(或某一块)倒下;② 如果前一块倒下,则一定能击倒后一块．让学生感受用有限的操作完成无限的任务的思想．如果希望多米诺骨牌全部倒下,则第一块要先倒下；如果希望多米诺骨牌从第五块倒下，则第一步应是先推到第五块．这里追问,旨在为后面数学归纳法的起始项n0做铺垫．

三、用数学语言描述问题

对于这样一类有无限项的问题,我们只用了有限的两步就完成了．如果这个方法能用于解决之前的数学问题,那就太好了．现在我们希望能用数学语言描述这种解决问题的方法．

问题5(1)“第一张”、“第一个”用数学语言如何表示?“某一个”如何表示?

(2)在第二步中,“如果前一块倒下,则一定能击倒后一块”．这里的“前一块”是指某一块,还是任意一块?(学生可以感知到是任意一块)

(3)数学语言如何描述任意一个?它的后一个如何描述?即如何表示一个数的后继数?前一个数加1即为后继数．

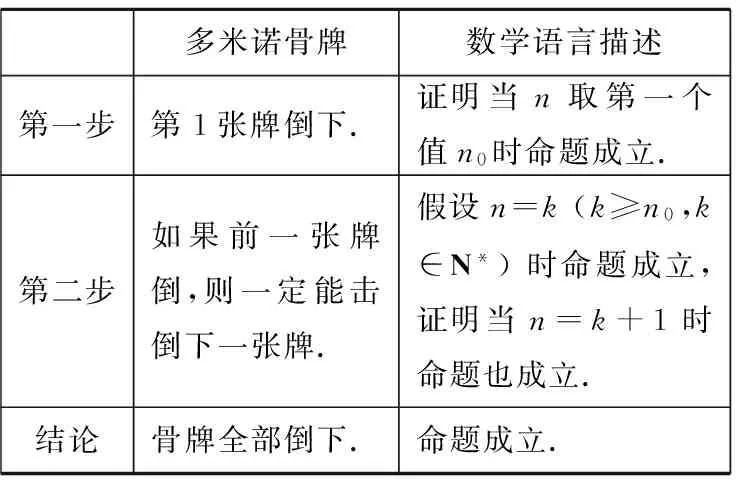
多米诺骨牌数学语言描述第一步第1张牌倒下.证明当n取第一个值n0时命题成立.第二步如果前一张牌倒,则一定能击倒下一张牌.假设n=k(k≥n0,k∈N*)时命题成立,证明当n=k+1时命题也成立.结论骨牌全部倒下.命题成立.

设计意图引导学生联想多米诺骨牌等游戏活动的条件,丰富学生对数学归纳法的表象,促进理解；同时通过表格,让学生更明确相关的类比，此过程为本节课的重点.若由之前的两个例子直接引出数学归纳法,虽然已是水到渠成,但却忽略了学生的自主建构过程,由特殊到一般的归纳推理过程,由有限到无限的思维质的飞跃过程．但若想让学生体验这些过程,必须把问题进行分解，通过问题的阶梯式提问,让学生完成了对两个步骤的数学语言描述,而此种描述即为数学归纳法的证明过程．至此,我们将这一解决问题的方法进行了数学化．

问题6数学归纳法用于证明一个与正整数有关的命题．证明过程中每一步骤的作用是什么?

我们要证明的命题不仅与正整数有关,而且证明一个新命题成立要充分利用上次的结果,把这次的推理建立在上次的结果之上,前后两个步骤存在有机的逻辑联系.这种思想在数学中就称为“递推”思想. 这主要体现在证明问题的第二步中, 因此这步骤称为“归纳递推”；第一步“n0”成立在证明中起到奠基的作用, 因此称为“归纳奠基”．

问题7每一步的作用是如何保证能实现的?

第一步的作用“归纳奠基”通过检验初始项来保证实现；第二步的作用“归纳递推”,是由n=k(k≥n0,k∈N*) 时命题成立,证明当n=k+1时命题也成立，即由条件n=k时命题成立,证明当n=k+1时命题也成立．特别强调在第二步的证明中,条件是什么?结论是什么?明确由什么证什么．

设计意图通过剖析每一步的作用,以及每一步具体做什么,达到剖析概念的目的．让学生加深对数学归纳法的理解．其中第二步的作用就是保证一种关系,条件是n=k时命题成立,结论是当n=k+1时命题也成立．至于n=k时命题是否真的成立,不是第二步需要关心的问题，所以这里用“假设”二字．而n=k时命题是否成立,是由第一步决定的．所以这里的k要满足k≥n0．至此,我们将数学归纳法进行了深入一步的剖析,完成了知识的建构．

四、用数学方法解决问题

问题8现在我们再来试试,用数学归纳法解决之前的数列问题.

设计意图将生活问题的解决方法数学化,这种方法不仅可以解决生活中的问题,具体共同特点的数学问题同样能解决．这也是我们寻找这种方法的目的所在——解决这样一类问题．从生活走向数学,让学生感受数学问题源于生活,解决问题的办法亦源于生活,当然数学更服务于生活．

五、例题讲解

问题9设n∈N*，下面对命题

1+3+5+…+(2n-1)=n2-1

的证明过程是否正确？

证明假设n=k时等式成立,即1+3+5+…+(2k-1)=k2-1;

那么,当n=k+1时,1+3+5+…+(2k-1)+(2k+1)=k2-1+(2k+1)=(k+1)2-1，即n=k+1时等式成立．

所以等式对一切正整数n均成立．

变式1用数学归纳法证明: 1+3+5+…+(2n-1)=n2(n∈N).

变式2能否把变式1的证明过程中第2步证明过程：

“当n=k+1时,1+3+5+…+(2k-1)+(2k+1)=k2+(2k+1)=(k+1)2，即n=k+1时等式成立．”

改换为下面的证明形式:

“1+3+5+…+(2k-1)

+[2(k+1)-1]

=1+3+5+…+(2k-1)+(2k+1)

=(k+1)2.”

为什么?

设计意图此部分练习由学生板书和教师投影规范书写相配合,对于最基本的步骤和格式进行规范要求，让学生明白用数学归纳法证明问题，两个步骤缺一不可．对于上面问题的讲解,在讲解的过程中利用多米诺骨牌和数列实例来解释,帮助学生理解．问题的设计,分别针对第一步和第二步,稍做变化,旨在深化概念,螺旋上升,以促进学生对数学归纳法深刻理解其思想本质．

《数学课程标准》中提到:数学是人类文化的重要组成部分．数学课程应适当反映数学的历史、应用和发展趋势,数学对推动社会发展的作用,数学的社会需求,社会发展对数学发展的推动作用,数学科学的思想体系,数学的美学价值,数学家的创新精神．

因此,通过本节课的教学,学生可以像数学家一样充分参与数学归纳法的形成和建构过程,数学归纳法的引入水到渠成．在教学过程中,学生学到的不仅仅是形式和抽象的理论,而是让数学归纳法的思想真正走入学生的内心世界．

我们的数学课堂教学更应关注数学思想对学生的熏陶以及学生数学素养的提高.只有掌握了数学的思想方法和精神实质,才能演绎出千变万化的生动结论,显示出无穷无尽的威力．