论基于学习理论的高等数学教学设计*1

席　阳　徐章韬

(华中师范大学　数学与统计学学院，湖北　武汉　430079)

论基于学习理论的高等数学教学设计*1

席阳徐章韬

(华中师范大学数学与统计学学院，湖北武汉430079)

摘要数学三个世界学习理论揭示了人类学习高等数学的认知发展顺序，为教师重新审视学生的认知发展过程、促进学生认知能力的发展提供了理论依据。文章以微分中值定理为例，从数学三个世界理论的视角出发，基于学习理论首先进行教学设计的前端工作，之后设计了具体的教学过程并进行教学实践，取得了不错的教学效果：教师上课自然流畅，学生学有所获。对于高等数学的学与教而言，这个学习理论的价值还值得进一步挖掘。

关键词学习理论；数学三个世界；教学设计；高等数学；微分中值定理

一、引言

高等数学虽然以其高度抽象性为显著特点，然而对于抽象知识的理解仍然需要直观事物的支持。高等数学的学习一般都会经历由直观感知到抽象提炼的过程。这个过程也对应了学习的两个层次：从初级学习到高级学习。因此对学生而言，他们的学习不能仅仅是达到初级学习的层次，只有达到高级学习的层次才能灵活运用所学知识。要达到高级学习的层次则要求学生能把握概念的复杂性，能根据具体情况，应用自己的知识、经验建构用于指导问题解决的图式[1]。如，微分中值定理是微分学的基本定理，同时也是微分学教学的重点和难点，它揭示了函数与其导函数之间的内在联系，开创了用导数研究函数的新道路并一直引导着函数性态的研究方向。已有的教学实践表明，由于学生认知能力发展不足，对于这三个微分中值定理的条件、结论、证明过程以及它们之间关系等的把握并不灵活，学习只达到了初级学习层次，导致在此后的学习和应用中存在一些困难。为了更好地促进学生认知能力的发展，提高学习层次，使教学获得更大的效益，我们需要深入剖析人类在学习数学时的认知发展过程是怎样的，也要清楚地知道人类是怎样通过学习来促进认知发展的。有学科特点的学习理论阐述了学习的本质和学习过程的规律，还就这些规律提出了一些切实有效的、可以促进学生学习的学习策略和教学策略等。教师需要在合适的学习理论的指导下进行数学的学与教。

对于人类是怎样学习的这一问题的不同理解使得学习理论出现分歧并产生了四大主要流派：行为主义、认知主义、人本主义和建构主义学习理论。不同的流派基于对学习过程及其规律的不同认识，提出了不同的学习策略和教学策略。(1)行为主义学习理论的核心观点是，学习是有机体在一定条件下形成刺激与反应的联结从而获得新经验的过程，强调强化对学习的作用，提倡用外部条件来控制学习过程[2]。(2)认知主义学习理论的探索视角由外部转移到了学习者的内部，强调学习过程应该是学习者积极主动的过程而不是被动地接受外部环境的刺激。学习是主体在已有经验的基础上通过“同化”和“顺应”新知识使得原有的认知结构进行组织与重组的过程。基于此，布鲁纳提倡“发现学习”，奥苏伯尔主张“有意义的接受学习”并提出了先行组织者策略；加涅将人脑与计算机类比，在融合了行为主义与认知主义学习理论的基础上提出了信息加工理论。(3)人本主义特别强调人的整体性，要求从整个人出发进行学习理论的探索，并且认为每个人都有自我实现的潜能，只是需要一个适当的环境[3]。(4)建构主义学习理论是认知主义学习理论的发展，强调学习是学习者与学习环境双向互动的过程。维果茨基对建构主义学习观的影响极大，提出了“最近发展区”理论并强调支架式教学模式。

这些学习/教学策略固然都有其合理性和有效性，但需要注意的是，它们的合理性和有效性体现在一般、普遍、广义上的学习，具有普适性却缺乏针对性，它们并没有结合具体的学科特点。在进行数学教学的时候，必须结合数学的学科特点，具体情况具体对待，才能使教学获得更高的效益。而英国华威大学(Warwick University)David Tall教授于2004年提出的数学三个世界学习理论就深刻地阐述了数学的学科特点。该理论是以建构主义理论为基础，结合当代认知科学、信息科学、新皮亚杰主义等研究成果创立的[4]。不仅如此，该理论还对数学认知发展的过程进行了深入的探索，揭示了人类学习数学时的认知发展顺序，为教师应该怎样促进学生的数学认知发展提供了理论依据。尤其值得关注的是该理论的研究对象包括了大学生以及数学家(这与建构主义等以儿童为主要研究对象不同)，因此其研究成果用于高等数学的教学更具合理性。

本文从数学三个世界这个认知发展理论出发，以微分中值定理的教学设计为例，探讨如何基于适当的学习理论进行教学设计及其实践。

二、依据学习理论做好教学设计的前端工作

“教师如何教将影响学生学到什么”是课堂学习的显著特征之一。为了做好教学工作，就要先进行课堂教学的预演——设计教学。教材是进行教学设计的重要依据。从字面上看，教材只是写出了要传授的知识点，对于知识点之间的联系等并没有明确地体现。所以为了做好教学设计，需要教师对教材进行深度剖析：不仅要知道本节课要学习的知识点有哪些，学习的侧重点在哪里，是否阐明了知识点之间的联系，还要分析教材是在怎样的学习理论的支撑下进行行文的，这样行文对学生的学习有哪些好处；是否教给了学生某些数学思想和方法，同时又向学生展现了怎样的数学文化等等。此外，对教材进行解读也是为了在进行教学设计时对选定的教学内容做序列化安排，使之既合乎学科本身内在的逻辑序列，又合乎学习者认知发展的顺序，从而把学习材料的知识结构与学习者的认知结构有机地结合起来[5]，为课堂教学的顺利展开打下良好的基础。

(一)依据学习理论解读教材，让学生学会发现数学

教材的行文方式使我们看到了做数学的一般套路。在高等数学教材中，微分中值定理一般是这样行文的：首先，引入学习微分中值定理的有力工具——费马引理，自然产生驻点的概念和性质。然后，用微分学的语言把观察到的特殊几何现象描述出来，就得到了罗尔定理。接着，把罗尔定理一般化，得到拉格朗日中值定理。最后，改变拉格朗日中值定理中函数的表达形式，获得柯西中值定理。教材行文方式的逻辑主线使我们学习到了做数学研究的一般程序：从平凡出发(观察)—选用适当的工具(费马引理、分析的语言)—平凡的结论—结论一般化或特殊化—结论再形式化。“授之以鱼不如授之以渔”，这条逻辑主线可以帮助学生在学习和研究数学的道路上有章可循，有法可依，学会学习。

从学习理论出发可以更好地理解教材，教给学生发现数学的方法。教材的行文方式层层递进，后面定理的学习都以前面学习的定理为出发点，前面学习的定理为后面定理的学习奠定基础，新旧知识融合在一起，既指出新旧知识之间的相同点，又点明不同之处，有利于学生数学认知结构的扩充和完善。学习就是要求学生能够前后关联，以旧促新，化新为旧，这其实是建构主义学习理论的主张。更进一步，教学要提供有层次、有序列的素材使学生由必须依赖直观事物理解数学知识的初级学习层次，顺利地上升到可以脱离直观事物的支持，在抽象世界中学习数学的高级学习层次，促进认知结构的分化，从而提高认知能力。

Tall认为，人类数学认知结构的发展要经历三个过程，分别对应着三个不同的数学世界[6]。

1.第一个世界是“概念—具体化世界(Conceptual-embodied World)”

这个世界源自对物理世界和思维世界的感知。学习者基于个人头脑中已经建立起来的关于以往经验的连接，通过操作、反思来想象并不存在于物理世界中的事物。这就要求我们在教学中结合实际生活，善用学生的已有经验，引导学生进行充分的观察和思考。在引导学生观察时，应该有目的有计划，选择被观察的事物时，被观察事物应当具备这样一个重要特征：沟通性。一方面被观察事物的某些特征是学生可以根据自己当前已有经验进行合理描述的，另一方面被观察事物的这些特征可以为将要学习的新知识做铺垫，是沟通新旧知识之间的桥梁，这同时也体现了引导观察的目的性和计划性。比如我们在讲授微分中值定理的概念之前，可以引导学生观察图1：曲线弧AB是函数y=f(x)(x∈[a,b])的图像，并让学生描述观察到的几何现象：这是一条连续的曲线弧，除端点外处处有不垂直于x轴的切线，两个端点的纵坐标相等，在曲线的最高点处或最低点处曲线有水平的切线……这里的“连续的曲线弧”“水平切线”“最高(低)点”等被观察物的特征是学生可以准确描述的，也可以为后面学习罗尔定理做铺垫。

图1

2.数学第二个世界是“过程符号化世界”(Proceptual-symbolic world)

这个世界始于行为，并在反省抽象的过程中，利用符号将行为压缩成概念，形成图式，这些符号有助于学习者在过程和概念之间来回转换，有助于进行算术、代数、微积分等的计算和操作。在这个世界里，物理操作中蕴含的道理被凝聚压缩成心理操作，实现了数学学习由过程到对象的飞跃。这要求我们在教学中要充分运用现有的工具和语言把观察到的现象刻画出来。在进行微分中值定理概念教学的时候，以学生有意义建构过的费马引理为工具，用分析的语言描述观察到的几何图形，得到罗尔定理的条件和结论，实现由过程到对象的飞跃。在对罗尔定理中的特殊条件“f(a)=f(b)”一般化后，仿照罗尔定理的发现模式，让学生用分析的语言描述图2，获得拉格朗日中值定理。

图2

3.第三个世界是“形式公理化世界( Formal-axiomatic World)”

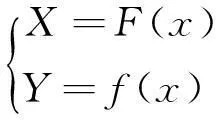
从微分中值定理的发现与学习过程中可以看到，与初等数学相比，高等数学中的很多概念已经不能从客观世界中找到其现实依据，一般都是经过对客观事物进行初步抽象后进行再抽象获得的，已经完全脱离了现实意义，形成了自己独特的符号化、形式化表达方式，不能为大多数人所直接理解。而且高等数学研究的是更加本质的、过程性的、多变量的数学过程和数学规律，得到的定理、定义、运算法则等一般都有严格的使用条件和适用范围，更不易被大多数人直接感知和运用。数学三个世界的理论研究了抽象知识的形成和转化过程，并把形式化推理作为最终目标[7]8-11，由高等数学的种种特点来看，它从本质上把握了高等数学不同于一般学科的特点，非常恰当地解释了人类在学习高度抽象的数学知识时的认知发展过程，为教师进行教学设计提供了新的视角。

(二)依据学习理论解读教材，让学生学会化归与证明

化归思想在数学思维与数学方法论中占有非常重要的地位，是解决数学问题非常常用的一种方法和手段。匈牙利数学家路莎·彼得在《无穷的玩艺》一书中写道：数学家们往往不是对问题进行正面的攻击，而是不断地将它变形，直到把它转化为已经得到解决的问题[8]。比如连著名的费马大定理证明的获得都要归功于各种转化思想。数学方法论中所论及的“化归方法”是一种间接解决问题的方法。它在解决数学问题中的作用就在于转化，把待解决或未解决的问题进行变形、分割、映射，或简单化、或熟悉化、或具体化、或正难则反化，直至归结到一类已经能解决或比较容易解决的问题中去[9]。鉴于拉格朗日中值定理和柯西中值定理与罗尔定理的关系，我们采取化归的方法来证明这两个定理。

在定理的证明中，我们设计选取费马引理为证明工具，后面所有定理的证明均依托于费马引理展开。费马引理体现了极值原理的重要性以及从不等到相等的辩证性：极值点处的值虽然可以最大或最小，但其导数值却是零。罗尔定理的证明设计主要是依据极值点处切线的斜率为零得到的，充分体现了极值原理的重要性。由于拉格朗日中值定理是罗尔定理的特殊条件一般化后得到的，柯西中值定理又是拉格朗日中值定理的推广，它们与罗尔定理之间都有密切联系，所以对于这两个定理的证明，在罗尔定理已经得证的基础上，我们考虑设计通过化归，将后面两个定理的证明都转化到罗尔定理的证明上。

具体来说，在拉格朗日中值定理中，函数f(x)不一定具备f(a)=f(b)这个条件，为此我们设想构造一个与f(x)有密切联系的函数φ(x)，使φ(x)满足条件φ(a)=φ(b)，然后对φ(x)应用罗尔定理，再把对φ(x)所得结论转化到f(x)上，从而证得所要的结果。在这里，就引出了一个新问题：如何构造辅助函数。

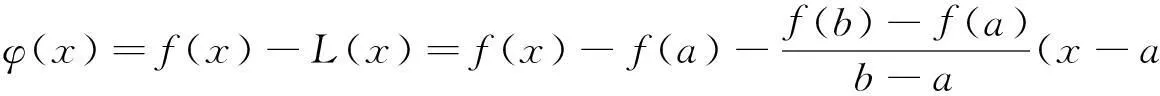
从上面的证明过程可以看出，拉格朗日中值定理的证明关键在于寻找不变量，利用不变量化归到罗尔定理的证明。无论直线AB倾斜与否，有向线段NM的值总是曲线与直线之差，这就是不变量。

柯西中值定理的证明实质与拉格朗日中值定理的证明是相同的，都是通过构造辅助函数将问题化归到罗尔定理。因此，学习在某种程度上就是复习。鉴于此，在三个微分中值定理证明的教学设计过程中，教师可先讲授罗尔定理的全部证明过程，然后让学生比较罗尔定理与拉格朗日中值定理之间的异同，重点讲授格朗日中值定理的证明过程中的新问题——辅助函数的构造方法，剩下的证明过程则交给学生。最后柯西中值定理的证明全部让学生自己来思考操作，教师不再赘述。这样在教授定理证明的过程中，教师的包办成分在逐步减少，学生的主动成分逐渐增加，教师与学生的相对地位一直处于动态平衡之中，教师的主导性和学生的主体性均可以得到落实，使新知识得到充分内化，学生能力和认知水平得到充分发展[10]，促进学生的学习由初级层次上升到高级层次。

三、依据学习理论进行教学

根据上述前端分析，我们进行了教学实践，将设计化成了实践，并取得很好的效果。下面是我们进行依据数学三个世界学习理论进行课堂教学的教案。

1.教学目标

深刻理解罗尔定理和拉格朗日中值定理及其几何意义，了解柯西中值定理；理解罗尔定理、拉格朗日中值定理、柯西中值定理三者的联系。让学生看到数学发生发展的过程，初步学会发现数学、证明数学的一些基本方法。使学生初步领略数学的美妙之处。

2.教学重点、难点

重点：微分中值定理中的拉格朗日中值定理及其应用。难点：拉格朗日中值定理中辅助函数的构造。

3.教学过程

第一课时：(1)开门见山，提出研究问题。我们要研究函数的性态，那么该从哪方面着手？虽然借助导数可以研究函数，但是函数在某一点的导数只能反映函数的局部特征，而我们需要了解函数在其定义域上的整体性态，如何用一个反映局部特征的量去研究整体的量呢？那么我们需要一个与导数密切相关但又能反映函数整体性态的工具，这就是我们本节课要学习的新工具——微分中值定理。(2)引导观察，寻找研究工具：山有最高点，有山谷，但只有平缓变化的山顶和山谷，才是平坦之处。此处意在引出费马引理这个研究工具。(3)几何现象数学化，得到基本结论——罗尔定理。(4)基本结论一般化，得到拉格朗日中值定理。(5)定理的应用及练习。(6)小结——留点悬念：如果改变函数的表达形式，拉格朗日中值定理将发生怎样的变化？

第二课时：(7)形式化，推广到柯西中值定理。(8)统一性，用行列式把这三个定理统一起来。(9)练习巩固。(10)总结。用图表的方式揭示三个定理之间的关联，并指出这是用导数研究函数的性态、体现“以直代曲”法的思想和方法的非常好的例子，需要好好体会。

四、分析与讨论

教学设计是沟通理论与实践的桥梁，是课堂教学活动是否有效的关键。这个教学设计经过了课堂教学的实践检验，教师感觉上课自然流畅，学生觉得学有所获。依据有数学学科特点的学习理论进行教学设计及教学实践，使学生对于高等数学知识的把握不只是停留在初级学习的层面，而是通过同化和顺应将新知识内化到数学认知结构当中，使认知结构组织或重组，促进认知能力的发展，从而使教学获得较大效益，提高了大学数学的教学质量。

第一，基于学习理论，对教材深入解读，可以灵活把握教材，准确定位教学目标。在知识与技能层面上，运用“深刻理解”“理解”“了解”等表达程度不同的词语对学生学习三个微分中值定理采取不同的要求，使得教学过程中有侧重，不会“眉毛胡子一把抓”。在过程与方法层面上，把数学的思想与方法的发生发展过程解构出来，使其过程符合学生认知的发生发展过程；在情感态度与价值观层面上，让学生充分感受到理趣、智趣而不肤浅的娱乐之处。教学需要有趣味，但这种趣味更多的是指理趣和智趣。“插科打诨”固然使学生当时感到有趣，但多年之后学生回首往事之时，才会发现根本没有学到什么。

第二，基于学习理论，对重点和难点有了更深切的把握。重点是指一节课的知识核心，难点是学生不易掌握的地方。拉格朗日中值定理处于三个微分中值定理的中枢，可以特殊化，也可以一般化。其证明过程还运用了在数学方法论中占有重要地位的化归法：显然是学生需要学习的重点。证明过程中辅助函数的构造十分巧妙，不易想到。学生能否构造辅助函数，学会化归，是他们能否从此节课中获得认知发展的重要标志。从学习的角度而言，这是过程—符号化学习阶段的良好载体，如果不充分经历这个阶段的学习，概念—具体化世界的学习将指向不明，就失去了其奠基性作用，形式化公理世界也将成为空中楼阁。有了学习理论的指引，再结合教师的专业素养，对何谓重点，何为难点将有自己独特的见解。

第三，基于学习理论，对教学过程有整体把握。“以学定教”是教育心理学的重要主张。从教学过程的设计来看，本节课的设计完全是由学习理论外化而成的。教学设计先由物理世界中的具体形象出发，再将其数学化，最后上升到形式化，引导着学生的数学认知从数学第一个世界，经历第二个世界，逐步发展到数学第三个世界，符合人类数学认知结构的发展规律，能使学生比较顺利地建构新知识的意义。在不改变教材内容和行文顺序的前提下，将整个微分中值定理的内容划分成由一条逻辑主线串起来的4个小知识点，而每一个小知识点的教学又都是由多个相互之间有密切联系的小问题组成，使得每一个问题的学习都控制在学生思维的“最近发展区”之内，让学生的学习呈现阶梯上升状。此外，考虑到一堂课中学生吸收新知识的“饱和度”，以拉格朗日中值定理为分界点将教学过程设计分为两个课时，给学生充分的时间消化吸收新知识。每个课时结束后都有一个关于微分中值定理的部分小结，先让学生对知识的认知形成一个个相对独立的认知节点，整个教学结束后再将有关节点关联起来形成关于微分中值定理完整的认知结构。即将分开讲述的三个中值定理再次融合成一个整体(用一个行列式将三个微分中值定理统一起来)，帮助学生将各个认知点相连接形成认知结构网络，立足于从整体把握微分中值定理，使得对于该定理的认知由部分上升到整体，提高了认知层次。

五、结语

数学三个世界理论深刻揭示了数学学习由浅入深必须要经历的三个过程，是关于人类数学认知发展研究的最新理论，给人们提供了研究认知发展的新视角，也可以重新审视学生的认知过程，以此创新教学理论、教学模式[7]8-11，为数学教学设计提供新的思路。对于高等数学的学与教而言，这个学习理论的价值还值得进一步挖掘。

参考文献：

[1]章建跃.建构主义及其对数学教育的启示[J].数学通报，1998(4)：2-7.

[2]刘启珍，杨黎明.学与教的心理学[M].武汉：华中科技大学出版社，2012.

[3]佐斌.论人本主义学习理论[J].教育研究与实验，1998(2)：33-38.

[4]周士民.数学三个世界的理论简介[J].数学通报，2012(3)：32-34.

[5]钟启泉，汪霞，王文静.课程与教学论[M].上海：华东师范大学出版社，2008.

[6]TALL D.A theory of mathematical grouth throuh embodiment，symbolism and proof[C].Annales De Didactique Et De Sciences Congitives，Irem de strasbourg，2006.

[7]周士民，聂立川，王君.认知发展研究新成果：David Tall的“数学三个世界理论”[J].数学教育学报，2013(3)：8-11.

[8]彼得.无穷的玩艺：数学的探索与旅行[M].朱梧槚，袁相碗，郑毓信，译.南京：南京大学出版社，1985.

[9]王子兴.数学方法论：问题解决的理论[M].长沙：中南大学出版社，1997.

[10]吴华，崔艳姣.基于数学三个世界的数学概念高效教学[J].数学教育学报，2015(3)：48-50.

(责任编辑李世萍)

*收稿日期2015-12-20

资助项目华中师范大学中央高校基本科研业务费项目“基于学习理论的信息技术与学科教科书的整合”(项目编号：CCNU15A06015)；华中师范大学重大科研课题及创新示范基地培育项目“TPACK视角下卓越数字化教师的培养研究”(项目编号：CCNUE2015-5).

作者简介席阳(1991-)女，河南新乡人，硕士研究生，主要从事数学教育研究.

中图分类号G642.4

文献标识码A

A Study on Instructional Design of Higher Mathematics Based on the Learning Theory

XI Yang，XU Zhang-tao

(School of Mathematics and Statistics，Central China Normal University，Wuhan，430079，China)

Abstract：The learning theory of the three worlds of mathematics reveals the cognitive development order of human learning higher mathematics，which provides a theoretical base for teachers to reexamine cognitive development process of students and to promote the development of students' cognitive ability.Taking the differential mean value theorem as an example，we begin with the first work of instructional design based on the theory of learning from the perspective of the Three Worlds of Mathematics theory，and then designed a specific teaching process and put it into the teaching practice.Finally，it can comes into a good teaching effect that teachers feel natural and fluent while teaching and students can learn something by this way.For the teaching and learning of higher mathematics，the value of this theory is worth further digging.

Keywords：learning theory；the three worlds of mathematics；instructional design；higher mathematics；the differential mean value theorem