变式教学在初中数学教学中的实证研究

李瑞

[摘 要] 在初中数学教学当中运用变式教学，能够拓宽数学思维，提升数学问题的解决能力，提高学生的综合素质.

[关键词] 变式教学；图形变式；类比变式；阶梯变式；拓展变式

随着我国教学体制的改革，学校教育的教学效果受到社会各界的广泛关注. 根据《新课程标准》中的相关要求，提升学生的综合素质是现今教学当中的一个重要任务之一. 对于初中数学教学而言，其应在教授学生相关数学知识的基础之上，注重对学生数学能力的培养. 根据相关研究结果显示，科学地使用变式教学能够较好地提升学生的数学思维.

初中数学教学当中的图形变式

初中数学教学当中的变式训练，其实质是将原题当中的已知条件进行合理地变换，从而使学生通过对题目的分析以及解答而得出新的结论，进而使得学生的数学思维得到拓展. 对于初中数学而言，运用图形进行解答类的题目相对较多，在学生习题当中所占据的比例也相对较大. 在初中数学的实际教学当中，教师应首先对图形的相关基础知识进行教学，使得学生能够对常见图形的基本概念有一个清楚的了解. 之后，教师可运用具体事物当中所包含的图形知识，帮助学生对各个平面图形之间的位置关系有一个直观的认识，从而帮助学生对相关知识进行深化了解. 而在解题的过程中，采用数形结合的方式往往能够较为快速地将问题进行解答. 因此，在训练的过程中，初中数学教师可将文字语言转化成数学语言，并要求学生从中提取出有价值的信息，帮助其提升数学能力.

例如，在笔者进行实际教学的过程中，教学“直线位置关系”的相关内容时，通常会把教室当中的具体事物作为教学素材，让学生拥有直观的认识. 在讲解直线平行的位置关系时，笔者会要求学生对教室当中存在的平行线进行观察并寻找，如上下两条墙角线、黑板的对边等. 而在对直线的垂直关系进行讲解的过程中，则会让学生观察墙角的三条线、黑板的相邻两条边等.

初中数学教学当中的类比变式

在初中数学教学的过程中，类比思想是其中较为重要的数学思想之一. 所谓类比，其实质是将两个或者多于两个相类似的题目就某个方面进行比较、总结，并对其解题规律进行总结，通过论证，将所得到的结论运用于其他类似题目的解题当中. 由此可见，通过类比所得出的结论首先应对其进行证明，之后才能应用到其他的数学问题当中. 同时，对相似问题分析得越多，其所得出的结论的准确性就相对越高. 对于其他数学思想而言，类比思想具有一定的创造性，可将该类问题的解题思路过渡到其他问题的解题方面. 例如，在对一元二次方程的解题方法进行讲解之后，教师可首先让学生对该类问题常用的解题方法进行总结，之后将该类方法试着运用到一元二次不等式的解题方面. 此外，通过对一元二次方程的变形，可引出抛物线、双曲线等圆锥曲线相关知识的讲解. 运用该类方法进行过渡讲解，不仅能使学生的知识得到充分地衔接，还能降低学生对知识的陌生感，提高学习效率.

例如，在笔者运用类比变式的方法进行实际教学时，首先会对“已知正方形ABCD的边长为2，P为直线CD上一点，若DP=1，则sin∠BPC的值为_____.”这一例题进行讲解，之后将其变换成以下三种类型，要求学生通过类比变式的方式进行解答.

变式1 在矩形ABCD中，AB=4，AD=6，P是直线CD上一点，若DP=1，则sin∠BPC的值为多少？

变式2 在直角梯形ABCD中，AD∥BC，∠ADC=90°，BC=8，CD=6，P是直线CD上一点，若DP=1，则sin∠BPC的值为多少？

变式3 在矩形ABCD中，AB=2，AD=3，点P是直线CD上一点，若DP=1，则sin∠BPC的值为多少？

初中数学教学当中的阶梯变式

在初中数学的实际教学过程中，教学质量的提升不仅要求教师对先进的教学理念进行掌握，并融会到当前的教学当中，还要求教师对教学方法进行改良，从而能够提高学生的学习兴趣. 此外，教师是否能够对本班学生就数学知识的认知规律进行掌握，也将是影响初中数学教学效果的一个关键因素. 一般而言，人们对知识的理解通常由易到难、由浅至深. 因此，在初中数学的教学期间，教师应首先对本班内学生的数学学习情况进行详细地了解，对其掌握数学知识的规律进行掌握，从而以由局部到整体等思想进行教学，以达到提升教学效果的目的. 如笔者在进行初中数学的实际教学过程中，通常会挑选本章节内容当中的典型例题作为教学素材，在课堂上对其解题思路、解题方法等方面的内容进行详细讲解，对其中所应引起注意的方面进行重点讲述. 之后，根据本章节的具体知识，选择具有一般性的例题要求学生进行作答. 如此一来，将会极大程度地降低学生对相关知识的理解难度. 同时，通过阶梯式变式教学，能够对学生思维的延伸起到极大的帮助作用.

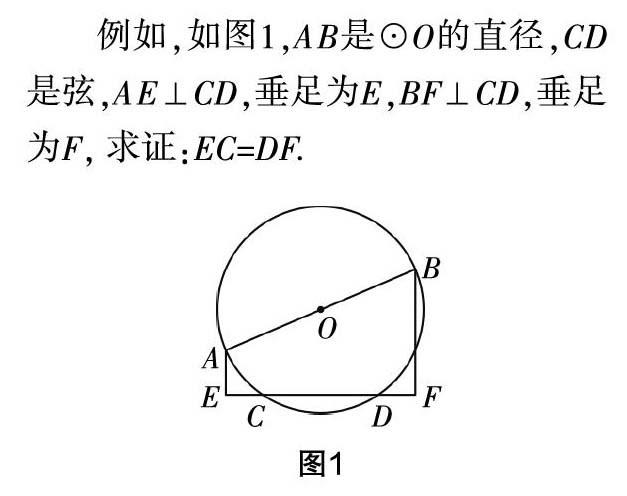
例如，如图1，AB是⊙O的直径，CD是弦，AE⊥CD，垂足为E，BF⊥CD，垂足为F， 求证：EC=DF.

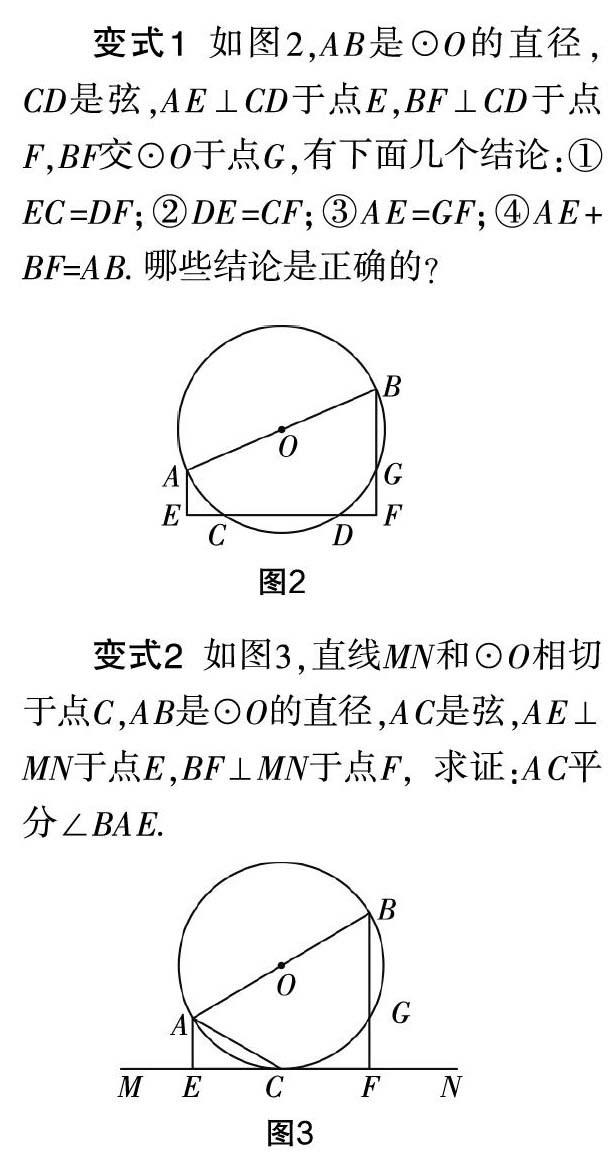
变式1 如图2，AB是⊙O的直径，CD是弦，AE⊥CD于点E，BF⊥CD于点F，BF交⊙O于点G，有下面几个结论：①EC=DF；②DE=CF；③AE=GF；④AE+BF=AB. 哪些结论是正确的？

变式2 如图3，直线MN和⊙O相切于点C，AB是⊙O的直径，AC是弦，AE⊥MN于点E，BF⊥MN于点F，求证：AC平分∠BAE.

初中数学教学当中的拓展变式

在中学教学阶段，数学是自然学科的一种. 所谓数学语言，是运用数学当中的符号、数量关系等对相关概念进行描述，其逻辑性相对较强. 因此，在对初中数学进行教学的过程中，教师应培养学生严谨的学风. 在运用较为开放性的教学方法对相关内容进行讲解的过程中，教师应对学生的逻辑思维能力进行充分考虑，切实从学生的角度出发，基于学生现有的思维层面进行拓展延伸，避免过度拔高而对学生的学习积极性产生负面的影响. 此外，根据相关研究结果显示，在初中数学的课堂教学期间，其教学效果的提升不仅依靠教师出色的教学能力，同时也依靠学生对课堂的融入. 因此，教师在教学期间除了运用合理的方法对学生的思考积极性进行调动外，还应激发学生热情地参与到课堂教学当中. 教师在对问题进行设置的过程中，应对问题的难度进行合理限制，以“跳一跳，能够着”为原则，严格依照学生的思维层面，采用循序渐进的方法对知识进行灌输，并对思考问题的角度等进行合理变化，帮助学生对知识之间的联系进行挖掘，从而达到提升学生思维能力的目的.

总而言之，在初中数学教学当中运用变式教学方式，能够在帮助教师提高教学效果的同时，激发学生热情地参与到课堂教学当中，使得学生能够在较为愉悦的环境当中实现数学知识的丰富，实现思维的拓宽，实现问题解决能力的提升. 因此，教师应根据教学实际情况，从学生的思维层面出发，以学生作为教学主体，科学地采用变式教学模式，引导学生对问题进行发现、解决，提高其综合素质.