变式教学，不可忽视的教学模式

倪广林

[摘 要]教师在教学过程中应该认识到变式教学的重要性，在提高学生数学成绩的同时培养他们的思维能力，促进学生全面发展。从概念的变式教学、规律探究题型的变式教学与一题多变题型的变式教学等入手去开展变式教学，可促进课堂教学效率的提高。

[关键词]小学数学 变式教学 教学策略

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）35-049

变式教学在小学数学中有着重要的作用，不仅能促进学生理解和掌握概念、规律和公式等知识，还有助于提高学生运用数学知识解决实际生活问题的能力。

一、概念类变式教学

学生在学习概念时往往把握不住关键点，导致记忆混淆。针对这种情况，教师可进行变式教学，将概念以多元化的形式呈现出来，从而促进加深学生理解与记忆。

例如，教学“梯形的认识”时，多数教师只是单纯地让学生识记梯形的概念，即一组对边平行但不相等，另一组对边不平行的四边形。在进一步学习直角梯形、等腰梯形的概念时，教师可这样进行教案设计：

首先，让每个学生都准备4张平行四边形纸片和1把剪刀，然后如下图所示将平行四边形分别剪成两个四边形（应注意不能剪成平行四边形）。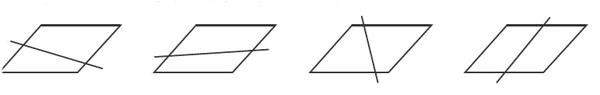

其次，为让学生进一步认识梯形，教师还可让学生准备一张半透明长方形纸和3个三角形，将半透明长方形纸和三角形分别重叠，可以得到如下图所示的四边形。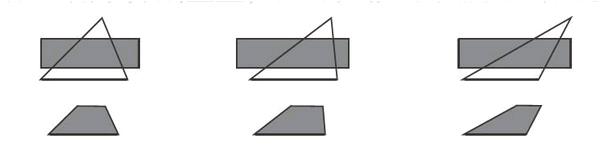

对于特殊的梯形，教师同样可以鼓励学生通过剪纸去发现它的本质，有效提高课堂教学效果。

上述案例中，教师将文字概念教学转化为直观的图形教学，使学生快速、有效地把握了概念的本质内涵，达到理解记忆的目的。概念的变式教学一方面为学生提供了探究的基础，使学生在动手操作的过程中真正融入课堂中；另一方面，它使学生对概念有了更加形象直观的认识，达到了事半功倍的效果。

二、规律探究类变式教学

规律探究类题目是小学数学教学的难点，其形式多变，对学生能力的要求较高。教师在教学过程中应该启发学生多思考，并由易到难开展变式教学，通过变式训练提高他们的思维能力与水平。

例如，按照排列规律，分别在（ ）里填上合适的数。

（1）4、7、10、13、16、（ ）、（ ）

（2）2、4、7、11、16、（ ）、（ ）

（3）2、3、5、8、（ ）、17、23、（ ）

这三道题的难度较小，学生很快找出了答案：第一题中，后面的数等于前一个数加3，所以括号应分别填上19和22；第二题的规律稍显复杂，需要在第一题的基础上进行变式，得出2+2=4，4+3=7，7+4=11，11+5=16，16+6=22，22+7=29，所以括号应分别填上22和29；第三题则是第二题的一个变式，两者有很大的联系。在学生熟练掌握该部分题目后，教师应让他们进一步练习一些简单的变式题，如2、4、8、14、22、（ ）、44、（ ）。

其次是中等难度的规律探究题，如找出下题中每组数之间的规律：2、4、8、14、22，3、4、6、9、13。

再次是高难度的找规律题目，如“一座拱形桥的两根柱子之间的距离是15米，现在桥的两边各有10根柱子，试求这座桥有多长。”这类应用题。

在规律探究类变式训练教学的过程中，教师应该遵循循序渐进的基本原则，帮助学生奠定坚实的基础，提高他们做题的速度与准确率，发展他们的思维。

三、一题多变类变式教学

单一题型的教学往往不能使学生真正掌握知识。对于某些数学问题而言，开展一题多变的变式教学能使问题被阐述得更透彻，可效提高学生的个人能力。

例如，教学“相遇问题”时，我出示三道题：（1）甲乙两地相距300米，客车从甲地开往乙地，每小时行使60千米，而小车从乙地开往甲地，每小时行使40千米。问两车同时发动，几小时后相遇？（2）客车与小车同时从甲乙两地相对而行，客车每小时行使60千米，小车每小时行使40千米，三小时后两车相遇，试求两地之间的距离。（3）客车与小车同时从甲乙两地相对而行，三小时后两车相遇，已知客车每小时行使60千米，试求小车每小时行使多少千米。第一题求的是时间，第二题求的是路程，第三题求的是速度，这三道题是路程问题的变式，可全方位促进学生掌握路程问题的解决方法，使学生对路程、时间、速度三者之间的关系有更深刻的认识。

教师在教学过程中应该多鼓励学生对题目换个说法，简化问题，以便快速把握题意，从而将问题解答出来。

综上所述，教师应该从学生的个人发展规律与知识水平入手，合理开展变式教学，使教学策略更契合学生的认知水平，提高他们学习的积极性与主动性。

（责编 吴美玲）