求一类非齐次微分方程特解的待定算子法

戴中林（西华师范大学数学与信息学院，四川南充637002）



求一类非齐次微分方程特解的待定算子法

戴中林
（西华师范大学数学与信息学院，四川南充637002）

［摘 要］给出了求一类非齐次微分方程L（D）y＝f（x）特解的待定微分算子解法．即通过求与方程相关的待定微分算子R（D），从而得出非齐次微分方程的特解y＝R（D）f（x）．

［关键词］非齐次微分方程；特解；待定微分算子；解法

1　引 言

对于一般线性非齐次微分方程L（D）y＝f（x）特解的求法，有关教材上已有介绍，当f（x）仅为x的幂函数，指数函数，三角正弦或余弦函数时一般应用算子解法［1］或待定系数法［2］，亦可用文［3］或其他的方法［4－7］解决，但这些解法较为繁琐．下面介绍一种求非齐次微分方程特解的待定算子法．即不通过积分运算，也无需按一般教材上的算子解法去定义微分算子L（D）的逆算子1／L（D）以及相关的性质和定理，而仅用微分的方法即通过求与微分方程相关的待定微分算子R（D），即可得到非齐次微分方程的特解y＝R（D）f（x）．

非齐次微分方程一般形式为

其中各项系数p1，…，pn均为常数，f（x）仅为x的幂函数，指数函数，三角正弦或余弦函数等．则上述方程对应的微分算子方程为

若已知方程L（D）y＝0的特征方程有n个特征根λ1，…，λn（可为等根），则该方程可记为或简记为

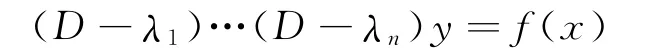
下面仅研究微分方程（1）的特解的求法

2　主要结果

定理1 微分方程L（D）y＝f（x）有解y＝R（D）f（x）的充要条件是存在微分算子R（D），当L（D）f（x）≠0时，有下式成立

证 必要性．设微分方程（1）有解y＝R（D）f（x），其中R（D）是待定微分算子，代入方程（1）得

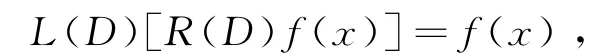
由微分算子乘积的可换性即得

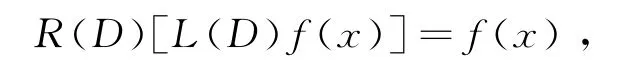
其中L（D）f（x）≠0．

充分性．若L（D）f（x）≠0，且有

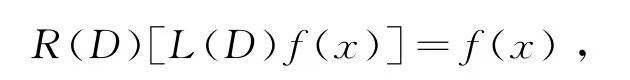
即存在微分算子R（D）满足方程

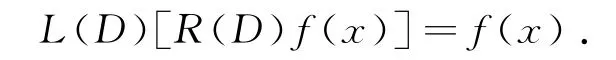
故可取y＝R（D）f（x），且满足微分方程L（D）y＝f（x），即方程（1）有解y＝R（D）f（x）．

在定理1中，若L（D）f（x）≡0，则本定理不可用．可用下面定理2求解．

定理2 微分方程L（D）y＝f（x）有解

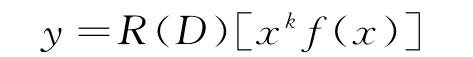
的充要条件是存在微分算子R（D），当L（D）xkf（x）≠0时，有下式成立

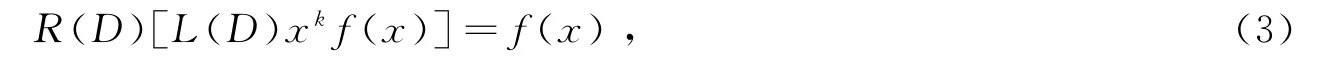
其中k＝1，2，…，n是齐次方程L（D）y＝0的特征方程的根的重数．

证 令F（x）＝xkf（x），仿定理1证明．

由上述定理可得到下面的求解公式．

推论1 若方程L（D）y＝0的特征方程有n个互异的特征根λ1，…，λn，且a不是特征方程的根，则方程L（D）y＝eax的解为

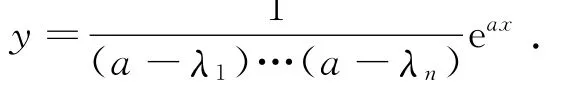
证 因方程L（D）y＝0的特征方程有n个互异的特征根λ1，…，λn，由定理1

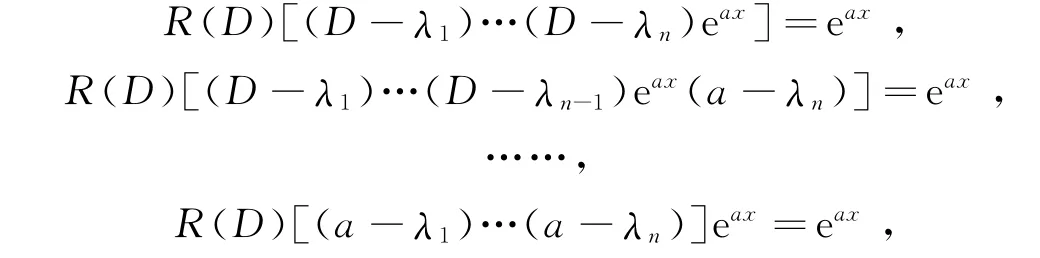
取

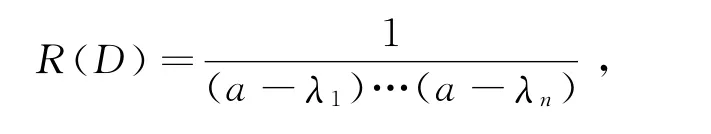
即得

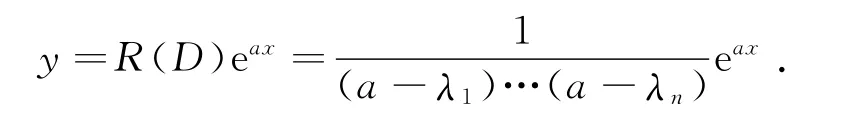
推论2 若方程L（D）y＝0的特征方程有n个互异的特征根λ1，…，λn，设a＝λ1是特征方程的单根，则方程L（D）y＝eax的解为

证 因方程L（D）y＝0的特征方程有n个互异的特征根λ1，…，λn，且a＝λ1为特征方程的单根．由定理2

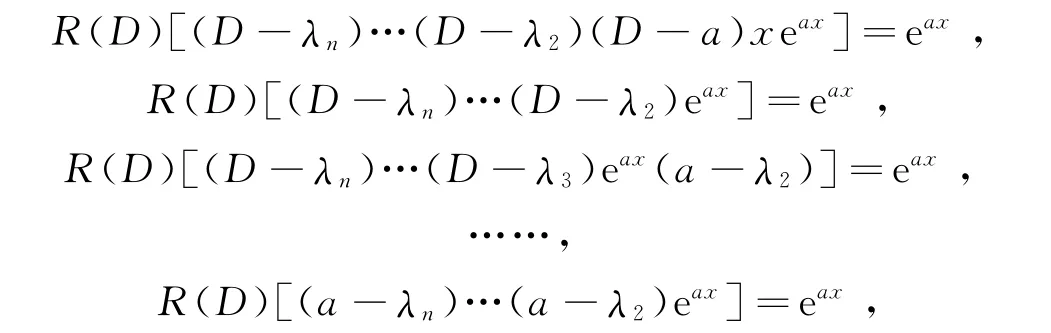
取

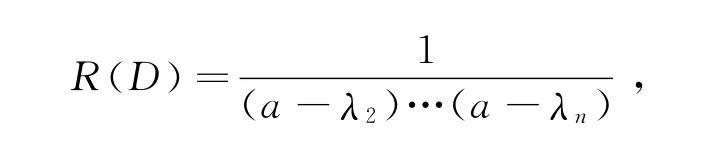
即得

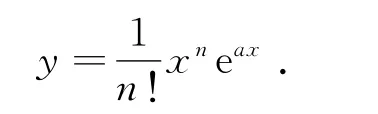
证 因方程L（D）y＝0的特征方程有n重根λ0，且a＝λ0，由定理2

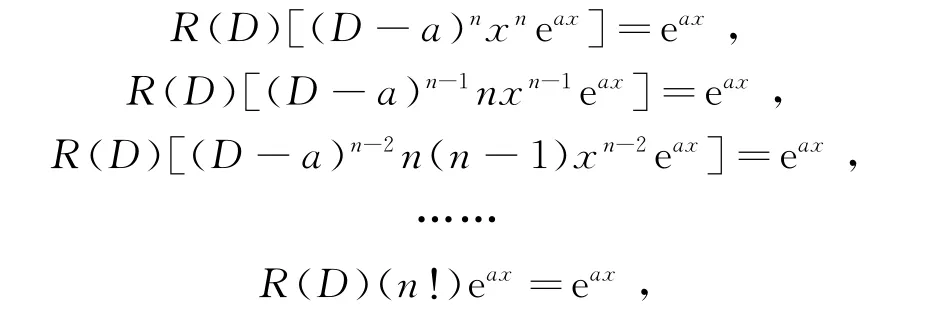
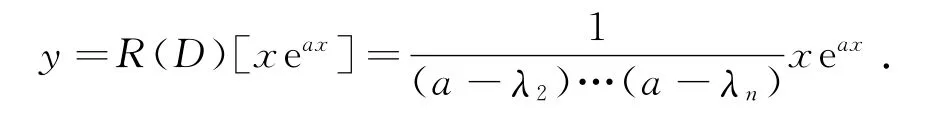
推论3 若方程L（D）y＝0的特征方程有n重根λ0，设a＝λ0，则方程L（D）y＝eax的解为，即得

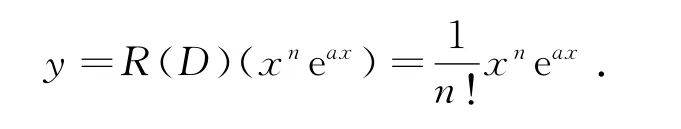
3　例 子

例1 求方程y（4）＋y″＋y＝x3的特解．

解 由定理1

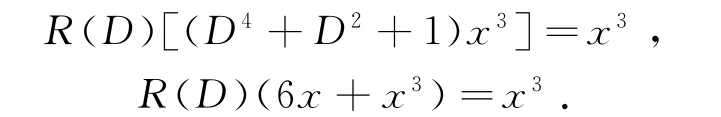
因方程中x的次数为三次式，可设

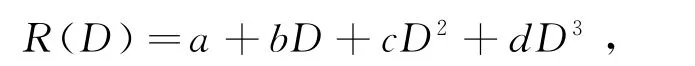
代入上式可求得

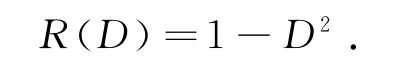
故原方程特解为

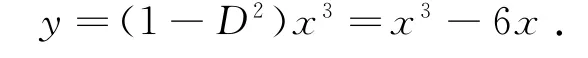
解法1 原方程即

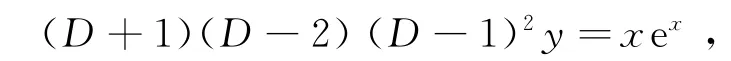
其自由项中a＝1是特征方程的二重根，故由本方法的定理2

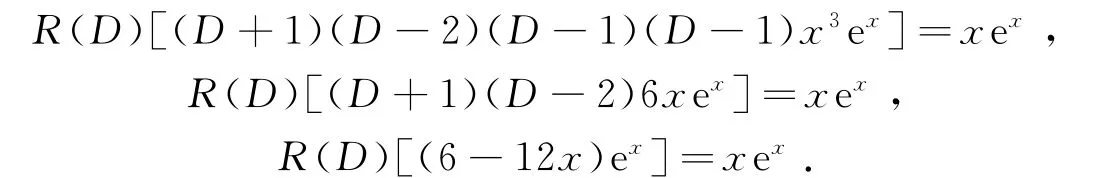
令R（D）＝a＋bD代入求得

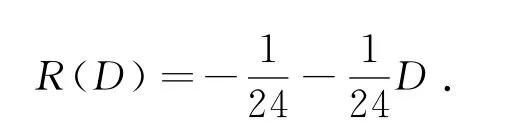
故原方程特解为

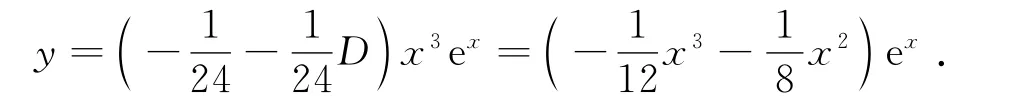
解法2 用传统的算子解法求解．原方程特解为

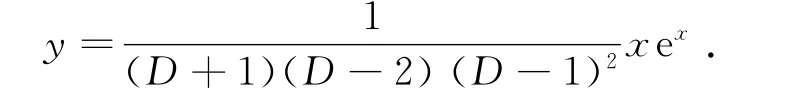
可由文［8］的方法将算子分式分解成部分算子分式

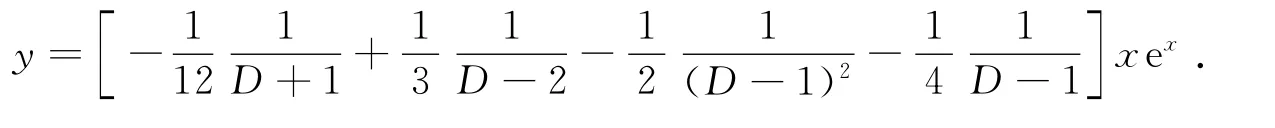
由逆微分算子性质，得

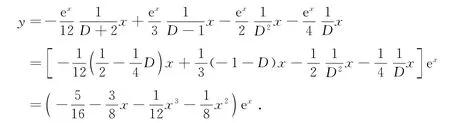
因前两项已包含在通解中，故特解为

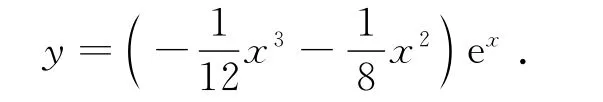
例3 求方程y″＋y＝xsinx的特解．

解法1 原方程即（D2＋1）y＝Imxei x，其自由项中a＝i是特征方程的单根．由定理2

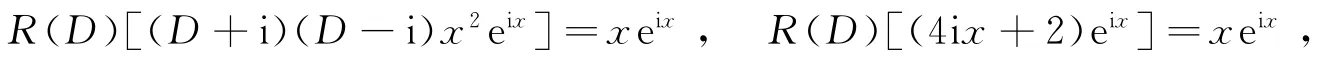
令R（D）＝a＋bD代入前式，即求得

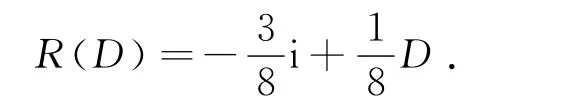
故原方程特解为

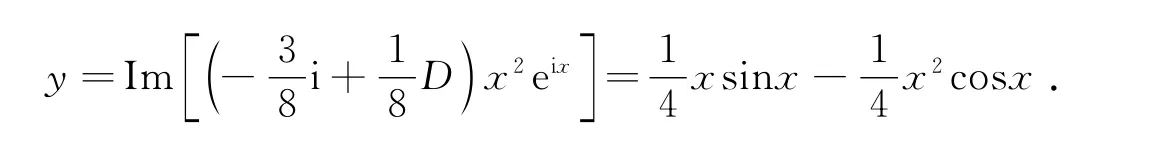
解法2 应用文［3］的方法求解，由常数变易法，设

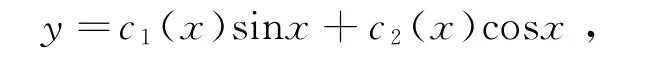
可得增广矩阵B（x），并对其进行初等变换，

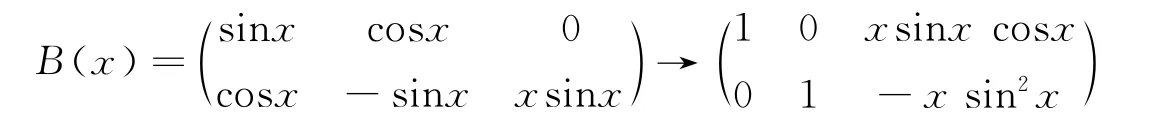
故有

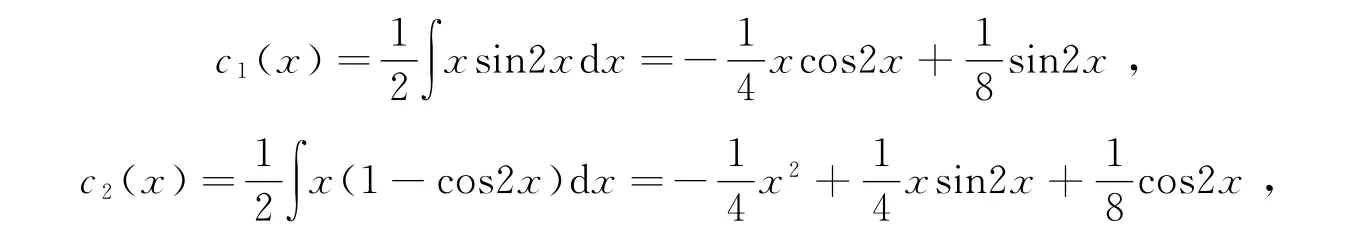
故

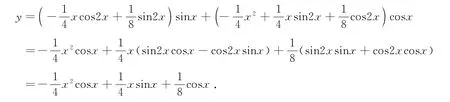
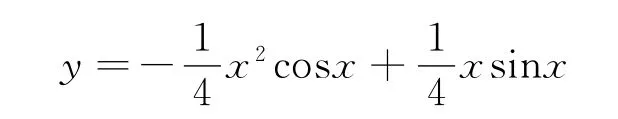
为原方程的一个特解．

从上述例2，例3的对比解法可看出本方法在实际计算时较其他方法是相当简便的．已包含在通解中，故取

［参 考 文 献］

［1］ 王柔怀，伍卓群．常微分方程讲义［M］．北京：人民教育出版社，1963：122－131．

［2］ 四川大学数学系高等数学教研室．高等数学（第三册）［M］．北京：高等教育出版社，1990：246－250．

［3］ 戴中林．求高阶非齐次微分方程（组）特解的矩阵解法［J］．大学数学，2013，29（6）：125－129．

［4］ 刘玲，苏农．n阶常系数非齐次线性微分方程的降阶解法［J］．大学数学，2012，28（6）：91－95．

［5］ 肖氏武．用算子升阶法求一类微分方程的特解［J］．高等数学研究，2010，13（4）：61－62．

［6］ 陈新明，杨逢建．用逆微分算子法求n阶常系数线性一般非齐次微分方程特解公式［J］．数学实践与认识，2004，34（3）：120－124．

［7］ 王隽．常系数线性非齐次微分方程的算子解法［J］．大学数学，1993，10（4）：204－206．

［8］ 戴中林．一类有理分式积分的解法［J］．高等数学研究，2013，16（6）：18－20．

Solving the Undetermined Differential Operator Method for Solving
the Special Solution of Non－Homogeneous Differential Equation

DAI Zhong－lin
（Mathematics and Information Institute，China West Normal University，Nanchong Sichuan 637002，China）

Abstract：The solutions of the special solutions for a class of non－homogeneous differential equations are given．Namely，the special solution of the non－homogeneous differential equation is obtained by solving the undetermined differential operator．

Key words：non－homogeneous linear equation；special solution；uncertain differential operator；solution

［收稿日期］2015－01－10

［中图分类号］O175．1

［文献标识码］C

［文章编号］1672－1454（2016）01－0096－05