三阶Hermite插值算子在Orlicz空间内的加权逼近

张思丽， 吴嘎日迪（内蒙古师范大学数学科学学院，呼和浩特010022）



三阶Hermite插值算子在Orlicz空间内的加权逼近

张思丽， 吴嘎日迪
（内蒙古师范大学数学科学学院，呼和浩特010022）

［摘 要］研究了修正的加权三阶Hermite插值算子在Orlicz空间的逼近性质，利用加权连续模、Hardy－Littlewood极大函数、Hölder不等式等工具给出了该插值算子在Orlicz空间内的逼近度估计．

［关键词］连续模；Orlicz空间；Chebyshev多项式；三阶Hermite插值算子

1　引 言

对于二阶Hermite插值算子及其导数的逼近性质在文献［1，2］中已有研究，近年来，人们转向对拟Hermite插值算子的导数逼近［3］及三阶Hermite插值算子的导数逼近［4］的研究．

设

为n阶第一类切彼晓夫多项式Tn（x）＝cos（narccosx）的全部零点．对任意的三阶Hermite插值算子［4］定义如下：

其中

修正的加权三阶Hermite插值算子：

本文将讨论修正的加权三阶Hermite插值算子在Orlicz空间内的逼近性质．文中用M（u）和N（v）表示互余的N函数，关于N函数的定义，Orlicz空间的定义及相关性质见［5］．文中是 Orlicz范数，定义如下：

文中C表示常数，但在不同处可以表示不同的值．

2　若干引理

引理1

得

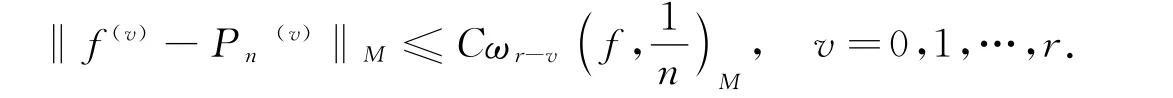
引理3［6］对，有

其中ω（f，t）M是Orlicz空间内通常意义下的连续模．

引理2［7］对任意的存在n次代数多项式Pn（x），使得

3　主要结果

证

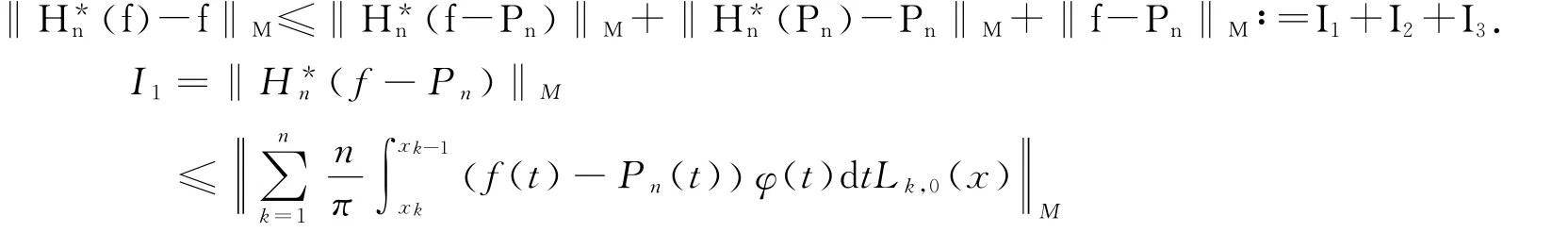
由Hölder不等式及引理2得

由u（t）在xk，xk－1

［］上几乎处处有界知

同理可得

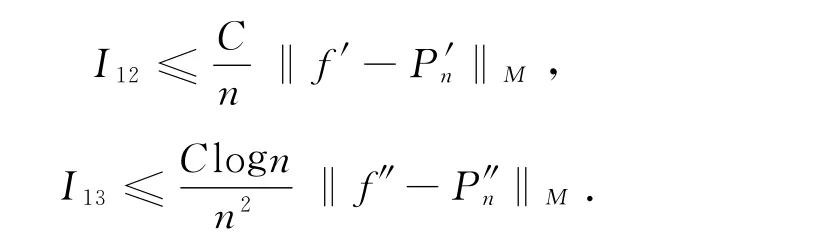
下面估计I2：

由Holder不等式及u（t），v（t）在xk，xk－1［］上几乎处处有界知

其中θP′n（x）是P′n（x）的Hardy－Littlewood极大函数，由Hölder不等式及v（x）在［－1，1］上几乎处处有界知

同理可得

由引理2直接可得

［参 考 文 献］

［1］ Vertesi P，Xu Y．Mean convergence of Hermite interpolation revisited［J］．Acta Math Hungar，1995，62（2）：185－210．

［2］ 崔鑫，曹莉，许贵桥．Hermite插值算子在加权Lp范数下的导数逼近［J］．天津师范大学学报（自然科学版），2009，29（2）：1－4．

［3］ 王鑫，崔然．Hermite插值算子在加权Lp范数下的导数逼近［J］．保定学院学报，2011，24（3）：19－23．

［4］ 夏颖，许贵桥．三阶Hermite插值算子在加权Lp范数下的导数逼近［J］．天津师范大学学报（自然科学版），2010，30（1）：1－6．

［5］ 吴从炘，王廷辅．奥尔里奇空间及其应用［M］．哈尔滨：黑龙江科学技术出版社，1983：1－78．

［6］ 谢庭藩，周颂平．实函数逼近论［M］．杭州：杭州大学出版社，1998：257－347．

［7］ Wu Garidi．On approximation by polynomials in Orlicz spaces［J］．Approx．theory ＆its Appl．，1991，7（3）：97－110．

［8］ 吴晓红，吴嘎日迪．Hermite插值算子在Orlicz空间内的逼近［J］．大学数学，2014，30（2）：7－10．

Weighted Approximation of the Third Order Hermite Interpolation Operators in Orlicz Space

ZHANG Si－li， WU Ga－ri－di
（College of Mathematics and Science，Inner Mongolia University，Hohhot 010022，China）

Abstract：The properties of modified of the third order Hermite interpolation operators are studied in Orlicz space，we use the weighted modulus of smoothness，Hardy－Littlewood great function Hölder inequality as tools to estimate the approximation of the interpolation operators in Orlicz space．

Key words：modulus of smoothness；Orlicz space；Chebyshev polynomials；the third order Hermite interpolation operators

［基金项目］国家自然科学基金（11161033）；内蒙古师范大学人才工程基金（RCPY－2－2012－K－036）；内蒙古师范大学研究生科研创新基金（CXJJS14053）

［收稿日期］2015－05－29

［中图分类号］O174．41

［文献标识码］A

［文章编号］1672－1454（2016）01－0011－04