带两个形状参数的四次Bézier曲线的扩展

翟芳芳（合肥北城中学，合肥231131）



带两个形状参数的四次Bézier曲线的扩展

翟芳芳
（合肥北城中学，合肥231131）

［摘 要］给出了一组含有两个形状参数α，β的四次多项式基函数，是四次Bernstein基函数的扩展，分析了这组基的性质；基于这组基定义了带两个形状参数的多项式曲线，所定义的曲线不仅保留了四次Bézier曲线一些实用的几何特征，而且具有形状的可调性，在控制多边形不变的情况下，改变参数α，β的取值，可以生成不同的逼近控制多边形的曲线；通过分析该曲线与四次Bézier曲线之间的关系，给出了α和β的几何意义，并利用Bézier曲线递归分割算法给出了这种曲线的几何作图法，同时还讨论了曲线间的拼接问题．

［关键词］计算机应用；曲线设计；四次Bézier曲线；形状参数

1　引 言

以Bernstein基构造的Bézier曲线由于结构简单直观成为几何造型工业中表示曲线／曲面的重要工具之一［1］．但曲线的位置相对于控制点是固定的，如果要调整曲线的形状一般可借助有理Bézier曲线和有理B样条曲线中的权因子来实现，但有一定的缺陷，如权因子如何选取、权因子对曲线形状的影响不是很清楚、求导次数会增加及基求积不方便等［2］．

近年来，人们通过形状参数来调整曲线的形状，其所用方法主要是提高多项式次数以获得不同于Bernstein基且含有参数的基函数，进而构造相应的曲线，在不改变控制多边形的条件下实现对曲线的调控［3－8］，这样就增加了计算量，文献［9］实现了在保持多项式次数不变的情况下对三次Bézier曲线的扩展．

本文构造了一组带两个形状参数α，β的四次多项式基函数，是四次Bernstein基函数的扩展，并且保持了Bernstein基函数的次数不变．基于该组基函数所定义的曲线具有非常灵活的形状，四次Bézier曲线是它的一个特例．另外，通过分析这种曲线与四次Bézier曲线之间的关系，得出了形状参数α和β直观的几何意义，并借助四次Bézier曲线的递归分割算法给出了这种曲线的几何作图法．最后还讨论了曲线间的拼接，由曲线的拼接条件可以灵活地构造出G1连续或C1连续的组合曲线．

2　基函数的定义及性质

定义1 对于t∈［0，1］；α，β∈［－3，1］，称形如（1）式的关于t的多项式为带有参数α，β的四次多项式基函数，简称四次αβ－B基．

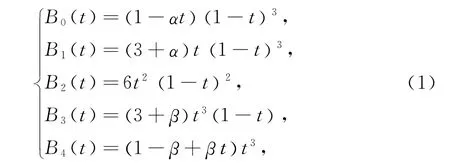
图1所示为α＝－1，β＝－1时的基函数图形．上述基函数具有如下性质：

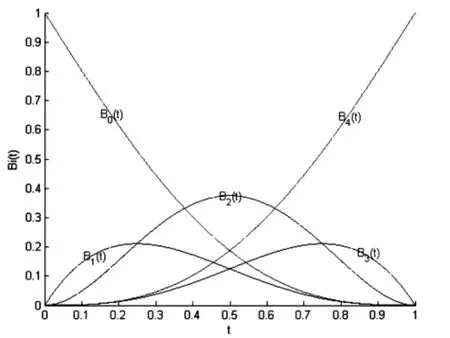
图1　基函数图形

性质2 拟对称性．即当α＝β时，

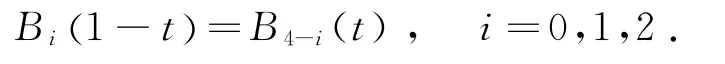
性质3 端点性质．B0（0）＝1，

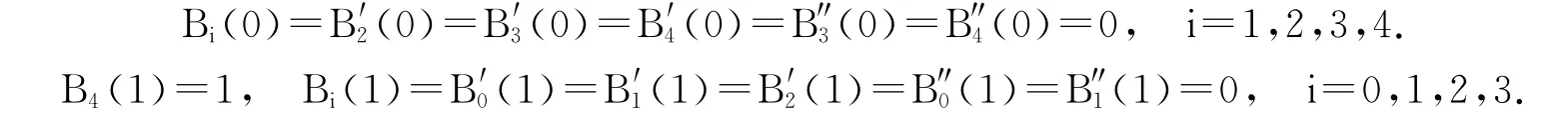
性质4 单峰性．即对每个基函数在［0，1］上有一个局部最大值．从图1就可判断，通过对基函数求导验证．

性质5 对参数α，β的单调性．即对固定参数t，B0（t）是α的递减函数，B1（t）是α的递增函数，B2（t）不随α，β的改变而改变，B3（t）是β的递增函数，B4（t）是β的递减函数．

性质6 当α＝β＝1时，则有

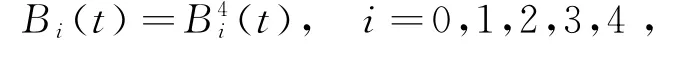
3　曲线的构造及性质

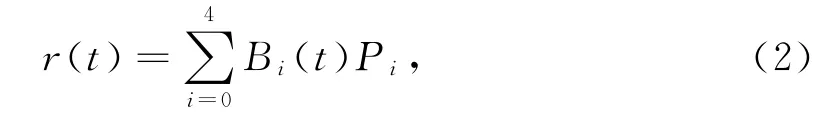
称（2）式所定义的曲线为带参数α，β的四次Bézier曲线，简称四次αβ－B曲线．显然，当α＝β＝1时，曲线（2）退化为四次Bézier曲线．图2所示为（α，β）取不同值时所对应的四次αβ－B曲线，其中1－（－1，－3）表示曲线1中α＝－1，β＝－3；

类似有

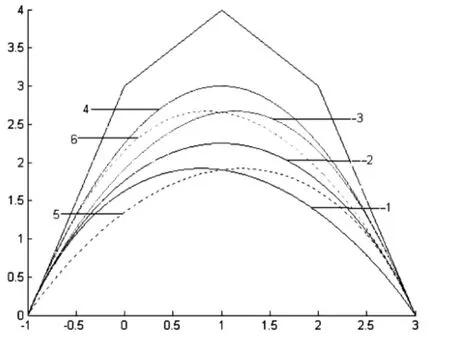
图2　不同参数值的曲线

由上述基函数的性质，不难得到曲线（2）具有以下性质：

性质1 端点性质．

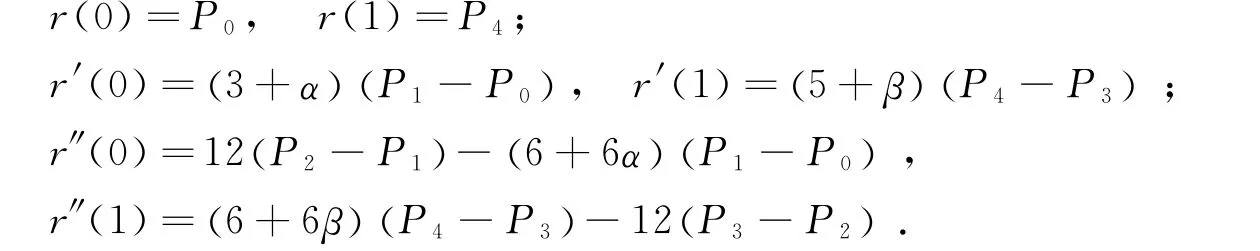
此性质说明曲线（2）插值于首末端点及与控制多边形的首末边相切，且在端点处的二阶导矢只与其相邻的3个控制顶点有关．

性质2 凸包性．由基函数的性质1，曲线（2）一定位于P0，P1，P2，P3，P4所围成的凸多边形内．

性质3 对称性．即当α＝β时，以P0，P1，P2，P3，P4为控制多边形的四次αβ－B曲线和以P4，P3，P2，P1，P0为控制多边形的四次αβ－B曲线是相同的，只是方向相反．由基函数的性质（2），可得

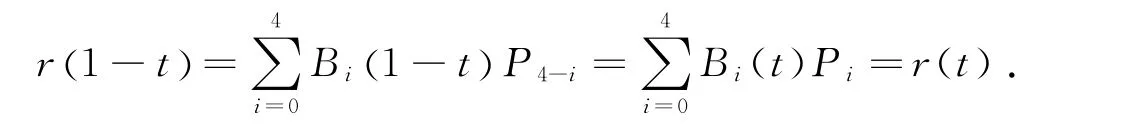
性质4 几何不变性和仿射不变性．曲线仅依赖于控制顶点而与坐标系的位置和方向无关，即曲线的形状在坐标系平移和旋转后不变；同时，对控制多边形进行缩放和剪切等仿射变换后，所对应的新曲线就是相同仿射变换后的曲线．

性质5 逼近性．由图2可以看出，当固定α，参数β逐渐增大（或减小）时，曲线逐渐靠近（或远离）控制顶点P3；当固定β，参数α逐渐增大（或减小）时，曲线逐渐靠近（或远离）控制顶点P1．此外，两个参数同时改变可实现更灵活的逼近方式．

4　曲线的几何作图法

由四次αβ－B基的表达式（1）可知

故四次α

β－B曲线的表达式（2）可用矩阵表示为

若令

由（4）式和（5）式可以得到，该曲线与表示它的四次Bézier曲线的控制顶点之间的关系式为

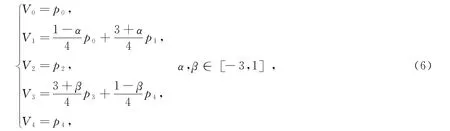
由（6）式可知，V1分边p0p1的比为（3＋α）∶（1－α），V3分边p3p4的比为（1－β）∶（3＋β），这就是形状参数α和β的几何意义（图3（a））．图中α＝－2，β＝0，p0p1p2p3p4为四次αβ－B曲线的控制多边形，V0V1V2V3V4为表示四次αβ－B曲线的四次Bézier曲线的控制多边形．

由（5）式可知，四次αβ－B曲线可以改写成四次Bézier曲线的形式，且二者的控制顶点之间有（6）式所示的显式关系．若已知四次αβ－B曲线的控制顶点，则由（6）式可以求出表示它的四次Bézier曲线的控制顶点，再利用四次Bézier曲线的几何作图法，经过四级递推，得到的最后一个点，即为四次αβ－B曲线上的点，如图3（b）所示，图中α＝β＝－2，t＝0．5．p0，p1，p2，p3，p4为四次αβ－B曲线的控制多边形顶点，V0，V1，V2，V3，V4为表示该四次αβ－B曲线的四次Bézier曲线的控制多边形顶点．图中的圆圈表示对四次Bézier曲线的控制多边形递推一次得到的点；三角形表示递推两次得到的点；菱形表示递推三次得到的点；星形表示递推四次得到的点，即为四次αβ－B曲线上的点p（t）．

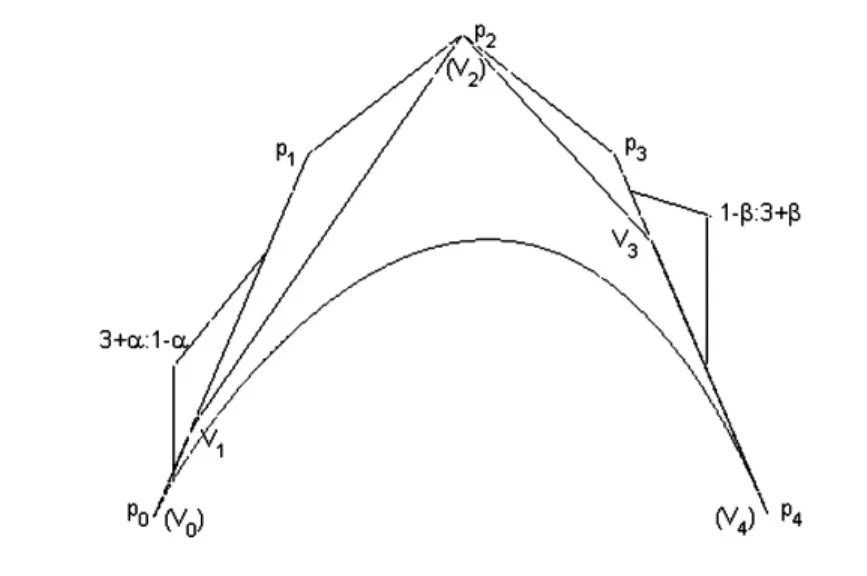
图3　（a）形状参数α和β的几何意义

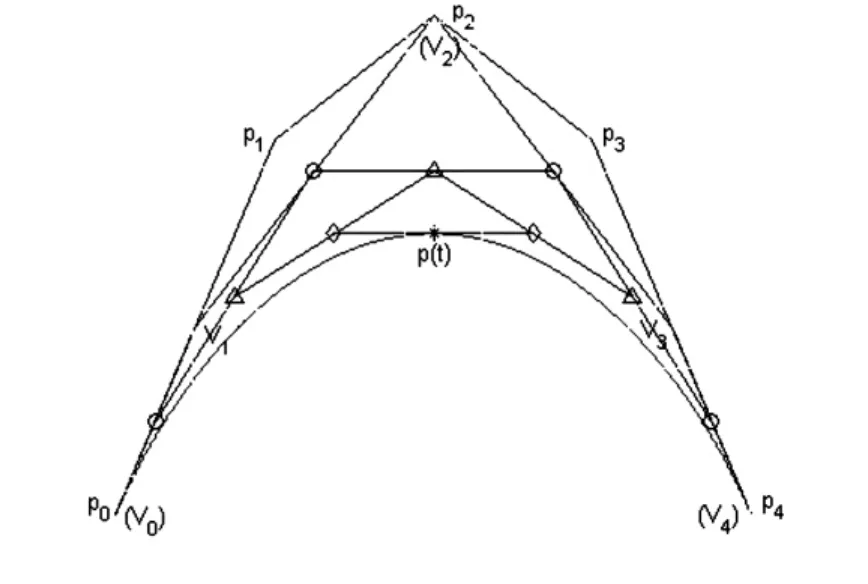
图3　（b）αβ－B曲线的几何作图法

5　曲线的拼接

由曲线的端点性质，两条不同的相邻四次αβ－B曲线可方便地进行G1和C1拼接．设两条相邻四次αβ－B曲线的表达式分别为

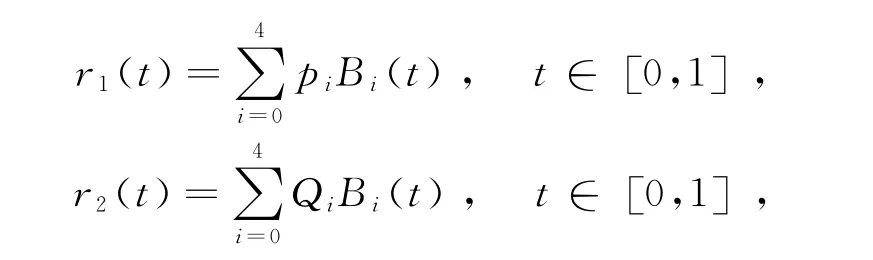
其中p0p1p2p3p4和Q0Q1Q2Q3Q4分别为r1（t）和r2（t）的控制多边形，且p4＝Q0，即满足位置连续．曲线r1（t）和r2（t）中基函数的形状参数分别为α1，β1和α2，β2，且αi，βi∈［－3，1］i＝1，2（）．

定理1 当且仅当顶点p3，p4（Q0），Q1共线且顺序排列，即Q0Q1＝δp3p4（δ＞0）时，曲线r1（t）和r2（t）之间G1连续．

证 由曲线的端点性质可知

而曲线r1（t）和r2（t）之间G1连续，当且仅当r′2（0）＝λr′1（1）（λ＞0），另

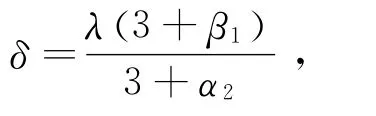
则由（7）式可以推出

即顶点p3，p4（Q0），Q1共线且顺序排列．这即为两曲线在连接点处G1连续的充要条件．

该定理表明，四次αβ－B曲线之间的G1连续条件与四次Bézier曲线之间的G1连续条件是一样的．

证 要使两曲线C1连续，则必有r′2（0）＝r′1（1），故由（7）式可知，此时（8）式中

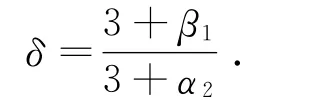
而两段四次Bézier曲线之间C1连续的充要条件为p3，p4（Q0），Q1共线且顺序等距分布，即Q0Q1＝p3p4．因此，从定理2可以看出，相对于四次Bézier曲线而言，采用四次αβ－B曲线来构造曲线组合，就意味着为曲线的性质控制提供了一个额外的自由度．

6　结 论

由四次αβ－B基函数构造的四次αβ－B曲线具有四次Bézier曲线的特征，如端点插值、端边相切、凸包性等．由于四次αβ－B曲线带两个形状参数，而每个形状参数可以固定不变、增大或减小，因此改变α 和β的值，可以灵活地实现8种逼近方式．四次αβ－B曲线可以由四次Bézier曲线来表示，借助Bézier曲线的几何作图法，可以方便地确定四次αβ－B曲线上的点．另外，由给出的拼接条件可以方便地构造出G1或C1连续的组合曲线．

［参 考 文 献］

［1］ 莫蓉，吴英，常智勇．计算机辅助几何造型技术［M］．北京：科学出版社，2004：56－62．

［2］ Marnar E．Shape preserving alternatives to the rational Bézier model［J］．Computer Aided Geometric Design，2001，18（1）：37－60．

［3］ Zhang Jiwen．C－curves：an extention of cubic curves［J］．Computer Aided Geometric Design，1996，13（2）：199－217．

［4］ 韩旭里，刘圣军．二次Bézier曲线的扩展［J］．中南工业大学学报（自然科学版），2003，34（2）：214－217．

［5］ 严兰兰，梁烔丰．带2个形状参数的3次多项式曲线［J］．合肥工业大学学报（自然科学版），2009，32（4）：572－576．

［6］ 朱秀梅，郭清伟，朱功勤．含多参数的四次Bézier曲线的扩展［J］．合肥工业大学学报（自然科学版），2008，31（4）：671－674．

［7］ 吴晓勤，韩旭里，罗善明．四次Bézier曲线的两种不同扩展［J］．工程图学学报，2006（5）：59－64．

［8］ 胡钢，等．Bézier曲线的新扩展［J］．计算机工程，2008，34（12）：64－66．

［9］ 秦新强，胡钢，张素霞．三次Bézier曲线的新扩展及其应用［J］．计算机工程与应用，2008，44（2）：112－115．

Extension of the Quartic Bézier Curve with Two Shape Parameters

ZHAI Fang-fang
（Beicheng High School of Hefei，Hefei 231131，China）

Abstract：A class of 4－degree polynomial basis functions containing two shape control parametersα，βis presented．It is the extention of quartic Bernstein basis functions．Properties of this new basis are analyzed and a polynomial curve with two shape parameters is defined based on it．The new curve not only hol ds many applied geometrical qualities of the quartic Bézier curve，but also can rectify the shape．When the control polygon is fixed，different curves approaching the control polygon with the changing of shape parameters are given．The geometrical meaning ofαandβare discovered by analyzing the connection of the new curve and the quartic Bézier curve．Meanwhile，the geometrical drawing method of the curve is given with the recursion segmentation algorithm of Bézier curve and the continuity condition of the curve is discussed．

Key words：computer application；curve design；quartic Bézier curve；shape paramet

［收稿日期］2015－09－29

［中图分类号］O243

［文献标识码］A

［文章编号］1672－1454（2016）01－0033－05