独立随机变量乘积的分布

刘继成， 胡晓山（华中科技大学数学与统计学院，武汉430074）



独立随机变量乘积的分布

刘继成， 胡晓山
（华中科技大学数学与统计学院，武汉430074）

［摘 要］得到了两个独立的任意分布随机变量乘积的分布函数的计算公式，该公式推广了参考文献［1］中定理1的结果．

［关键词］分布函数；条件期望；Lebesgue－Stieltjes积分

1　问题的提出

文献［1］中的定理1给出了两个随机变量乘积的分布函数的计算公式，其中要求一个随机变量是连续型随机变量，另一个是任意的随机变量，并在注3中举例说明该公式不适用于两个都是任意随机变量的情形．本文对此问题给予正面的解答，得到任意两个独立随机变量乘积的分布函数公式，该结果适用于［1］中定理1不成立的情形．

2　预备知识

需要下面条件期望的性质．

性质1 设随机变量X和Y独立，则对任意Borel可测函数f（x，y），

另外，需要下面特殊情形下Lebesgue－Stieltjes积分的计算公式．

性质2 设α（x）绝对连续，β（x）关于α（x）在开区间I上Lebesgue－Stieltjes积分存在，则

性质3 设α（x）为跳跃函数且在xk的跳跃为αk，β（x）关于α（x）在开区间I上的Lebesgue－Stieltjes积分存在，则

3　主要结论

定理1 设随机变量X和Y的分布函数分别为F（x）和G（x），且X和Y相互独立，则Z＝XY的分布函数H（x）为

其中等式右端的积分理解为Lebesgue－Stieltjes积分．由F（x）和G（x）的对称性，易知H（x）也等于

证 由全概率公式及条件期望的性质1，有

下面讨论几种特殊情况作为特例，这些公式在实际中应用更为方便．

（i）若G（x）在x＝0处连续，则Z＝XY的分布函数为

若G（x）连续，因为F（x）的不连续点至多可列个，所以

因此

若G（x）绝对连续，且G′（x）＝g（x），则

更进一步，若F（x）也绝对连续，且F′（x）＝f（x），则Z＝XY的密度函数h（x）为

（ii）若G（x）为跳跃函数，且在xk的跳跃为pk，则Z＝XY的分布函数为

更进一步，若G（x）在0连续，则

再进一步，F（x）绝对连续，且F′（x）＝f（x），则Z＝XY为连续型随机变量，其密度函数h（x）为

4　应用举例

例1 设随机变量U服从［－1，2］上的均匀分布，V的密度函数为

且U和V相互独立．记X＝max｛U，1｝，Y＝min｛V，2｝，求XY的分布．

解 容易计算，X和Y的分布函数分别为

注意到，当x＜0或者x＞2，dFY（x）＝0，以及FY（x）在x＝0连续，FY（0）＝0设XY的分布函数为H（x），由公式（1）得

因此，当x≤0，H（x）＝0．当x≥4，

当2≤x＜4，

当0＜x＜2，

例2 设随机变量X和Y的分布函数分别为

注意到G（x）在0连续，由公式（2），则Z＝XY的分布函数为

例3 设X服从参数为μ的指数分布，其分布函数为

Y服从参数为λ的Poisson分布，其分布列为

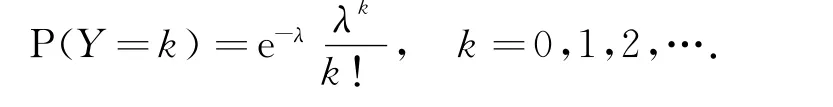
假设X和Y相互独立．注意到，此时Y只取自然数，（5）式右端第二项为0，又因为Y的分布函数G（x）满足G（0－）＝0，因此（5）式右端第三项为0，且易知G（0）＝P（Y＝0），因此Z＝XY的分布函数为

注 本文通讯作者胡晓山，hxs＠hust．edu．cn

［参 考 文 献］

［1］ 刘洋，何璐，孙丽英，许贵桥．随机变量积的分布函数及其应用［J］．大学数学，2014，5（30）：112－115．

［2］ 严加安．测度论讲义［M］．2版．北京：科学出版社，2004．

［3］ Carter M，Van Brunt B．The Lebesgue－Stieltjes Integral：apractical introduction［M］．New York：Springer Press，2000．

The Distribution Function of the Product of Independent Random Variables

LIU Ji－cheng， HU Xiao－shan
（School of Mathematics and Statistics，Huazhong University of Science and Technology，Wuhan 430074，China）

Abstract：We give a computing formula to the distribution function of product of independent random variables，which extends the result of Theorem 1in the reference［1］．

Key words：distribution function；conditional expectation；Lebesgue－Stieltjes integral

［基金项目］华中科技大学自主创新研究基金（2014TS066）；华中科技大学教学研究项目（2015067）

［收稿日期］2015－06－30

［中图分类号］O211．5

［文献标识码］C

［文章编号］1672－1454（2016）01－0123－04