循环子空间的若干应用

谢启鸿（复旦大学数学科学学院，上海200433）



循环子空间的若干应用

谢启鸿
（复旦大学数学科学学院，上海200433）

［摘 要］从线性变换诱导的循环子空间出发，推导出了Cayley－Hamilton定理，并给出了循环子空间在相似标准形理论以及一些相关问题中的若干应用．

［关键词］线性变换；不变子空间；循环子空间；Cayley－Hamilton定理；有理标准形；Jordan标准形

设V是数域K上的n维线性空间，φ是V上的线性变换．对任意的非零向量α∈V，由α，φ（α），φ2（α），…张成的子空间C（φ，α）称为向量α关于线性变换φ的循环子空间，α称为循环子空间C（φ，α）的循环向量．由定义知道，C（φ，α）是φ的不变子空间，而且是包含向量α的最小不变子空间．

讲授相似标准形理论的传统方法是λ－矩阵的方法，这种方法在证明有理标准形和Jordan标准形存在性的基础上，还能教会学生如何计算上述两种标准形，所以对初学者来说是一个较好的选择．而如果要用几何的方法建立相似标准形理论，那么循环子空间将在这一过程中起到举足轻重的作用．例如，由Cayley－Hamilton定理可以得到全空间关于根子空间的直和分解，而每一个根子空间又可以分解为若干个循环子空间的直和，由此即可推导出Jordan标准形的存在性（参考［2］的§7．2．10）．虽然仍需要通过进一步的计算来确定Jordan标准形的形状，但循环子空间给予了Jordan标准形理论一个清晰的几何意义，让我们可以看清楚复杂问题的几何内涵．

按照近世代数（模论）的观点来看，V是多项式环K［x］上的模，即对任意的多项式f（x）以及任意的向量α∈V，K［x］关于V的作用可定义为f（x）·α＝f（φ）（α）．由于K［x］是主理想整区，故由主理想整区上有限生成模的结构定理可得V的K［x］－循环子模的直和分解．注意到V的K［x］－循环子模均可写成K［x］·α的形式，其中α是V中的某个向量，根据模结构的定义，上述循环子模就是循环子空间C（φ，α）．进一步，对应于V的K［x］－循环子模直和分解的不变因子组和初等因子组，可分别得到φ的有理标准形和Jordan标准形．因此，一个Frobenius块或一个Jordan块对应的子空间就是一个循环子空间．当然，即使不从较高的观点来建立相似标准形理论，一般的高等代数教材（例如［1］）也都会引入循环子空间的概念并阐述其几何意义，但通常篇幅不会太长，也很少探讨它的相关应用等．

在讲授完相似标准形理论后，作者在复旦大学数学科学学院本科生的高等代数习题课上引入了循环子空间的理论，阐述了它的几何意义，并且深入探讨了它在一些问题中的应用，得到了较好的教学效果．本文试将这些内容进行如下的总结．

以下总是假设V是数域K上的n维线性空间，φ是V上的线性变换．我们先证明关于循环子空间的两个引理．

引理1 设α是V中的非零向量，C（φ，α）是循环子空间．设di mC（φ，α）＝m，则｛α，φ（α），…，φm－1（α）｝是C（φ，α）的一组基．

证 设于是α，φ（α），…，φk－1（α）线性无关，但α，φ（α），…，φk（α）线性相关，故φk（α）是α，φ（α），…，φk－1（α）的线性组合．进一步用数学归纳法容易证明：对任意的i≥k，φi（α）都是α，φ（α），…，φk－1（α）的线性组合．因此｛α，φ（α），…，φk－1（α）｝是C（φ，α）的一组基，从而m＝dimC（φ，α）＝k，结论得证．

引理2 设α是V中的非零向量，使得V＝C（φ，α）（此时V称为循环空间，α称为全空间的循环向量）．设ψ是V上的另一线性变换且φψ＝ψφ，则

（i）ψ由它在循环向量α上的取值ψ（α）唯一确定；

（ii）存在多项式g（x）∈K［x］，使得ψ＝g（φ）．

证 （i）由引理1可知，｛α，φ（α），…，φn－1（α）｝是V的一组基．线性变换ψ由它在基向量上的取值唯一确定，又由φ，ψ的交换性可得ψ（φi（α））＝φi（ψ（α））（0≤i≤n－1），因此ψ由ψ（α）唯一确定．

（ii）设

令

则ψ（α）＝g（φ）（α），即线性变换ψ，g（φ）在循环向量α上的取值相同．又ψ，g（φ）都与φ可交换，从而由（1）可得ψ＝g（φ）．

先利用循环子空间来证明著名的Cayley－Hamilton定理．

证 任取非零向量α∈V，设dimC（φ，α）＝m，则由引理1可知，｛α，φ（α），…，φm－1（α）｝是C（φ，α）的一组基．设，

令

则g（φ）（α）＝0．容易验证φ限制在C（φ，α）上在基｛α，φ（α），…，φm－1（α）｝下的表示矩阵为多项式g（λ）的友阵

将｛α，φ（α），…，φm－1（α）｝扩张为V的一组基，则φ在这组基下的表示矩阵为

于是

证 先证充分性．设f（λ）是K上的不可约多项式，则与定理1完全相同的证明可得f（λ）＝g（λ）h（λ），从而只能是h（λ）＝1，于是

因此C（φ，α）＝V对任意的非零向量α都成立．．因此f（φ）（α）＝h（φ）g（φ）（α）＝0，再由α的任意性即得f（φ）＝0．

若V有一个非平凡的φ－不变子空间U，任取一个非零向量α∈U，则有C（φ，α）⊆U≠V．反之，若存在一个非零向量α∈V，使得C（φ，α）≠V，则C（φ，α）就是一个非平凡的φ－不变子空间．因此，V只有平凡的φ－不变子空间当且仅当对任意的非零向量α∈V，C（φ，α）＝V都成立，即V的任一非零向量都是全空间的循环向量．利用循环子空间的理论，还能给出下列命题的一个简单证明．

命题1 V只有平凡的φ－不变子空间当且仅当特征多项式

再证必要性．设f（λ）在K上可约，即f（λ）＝g（λ）h（λ），其中degg（λ）＜n，degh（λ）＜n，则由Cayley－Hamilton定理可得f（φ）＝g（φ）h（φ）＝0．注意到Kerg（φ）和Kerh（φ）不可能同时是零空间，否则g（φ）和h（φ）都是线性同构，这与g（φ）h（φ）＝0相矛盾．因此Kerg（φ）和Kerh（φ）至少有一个非零，不妨设Kerg（φ）≠0．进一步可设

其中m＜n，再任取0≠α∈Kerg（φ），则有

用数学归纳法容易证明：对任意的i≥m，φi（α）都是α，φ（α），…，φm－1（α）的线性组合，因此C（φ，α）的维数小于等于m，从而C（φ，α）≠V．

设φ的不变因子组为1，…，1，d1（λ），…，dk（λ），其中di（λ）是K上的非常数首一多项式，且di（λ）｜di＋1（λ）（1≤i≤k－1），则由有理标准形理论可知，存在V的一组基｛e1，e2，…，en｝，使得φ在这组基下的表示矩阵为有理标准形

其中F（di（λ））表示多项式di（λ）的友阵（形状见定理1的证明）．例如，若设

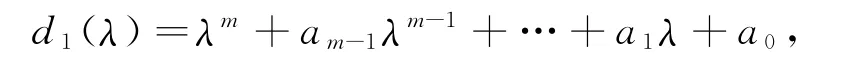
则有如下的关系图成立：

这说明第一个Frobenius块F（d1（λ））对应的子空间L（e1，e2，…，em）就是由e1生成的循环子空间C（φ，e1）．因此全空间V可以分解为若干个基向量生成的循环子空间的直和：

我们来看一个特殊情形．若φ的不变因子组为1，…，1，f（λ），即极小多项式等于特征多项式f（λ），则φ的有理标准形只含一个Frobenius块F（f（λ）），此时V＝C（φ，e1）就是一个循环空间．反之，若V＝C（φ，α）是一个循环空间，则由引理1可知｛α，φ（α），…，φn－1（α）｝是V的一组基，仿照定理1的证明可得φ在这组基下的表示矩阵为F（f（λ）），其中f（λ）是φ的特征多项式，也是φ的极小多项式．利用上述一一对应可得如下两个有趣的推论．

推论1 设A＝F（f（λ））为n次首一多项式f（λ）的友阵，B为同阶方阵，若AB＝BA，则存在次数小于n的多项式g（λ），使得B＝g（A）．

证 利用代数与几何之间的对应关系和引理2（2）即得结论．

推论2 设V是数域K上的n维线性空间，φ是V上的线性变换，α1≠0，α2，…，αm是V中的向量，满足

令

若g（λ）在K上不可约，则α1，α2，…，αm线性无关．

证 显然，U＝L（α1，α2，…，αm）＝C（φ，α1）是V的循环子空间．记φ在U上的限制为φ1，则U＝C（φ1，α1）也是一个循环空间．设φ1的特征多项式为h（λ），则h（λ）也是φ1的极小多项式．由假设可知g（φ1）（α1）＝0，故由引理2（1）可得g（φ1）＝0，再由极小多项式的基本性质可得h（λ）｜g（λ）．因为g（λ）在K上不可约，所以只能是h（λ）＝g（λ），于是U的维数等于degh（λ）＝degg（λ）＝m，从而｛α1，α2，…，αm｝是U的一组基，故必线性无关．

一个循环空间还可以分解为若干个循环子空间的直和，我们来看下面的命题．

命题2 设V是数域K上的n维线性空间，φ是V上的线性变换，f（λ）是φ的特征多项式．设存在非零向量α∈V，使得V＝C（φ，α）为循环空间，则以下结论等价：

（i）f（λ）＝P1（λ）m1…Pr（λ）mr，其中Pi（λ）（1≤i≤r）是数域K上互异的首一不可约多项式，mi（1≤i≤r）是正整数；

（ii）r＝max｛s∈Z＋｜存在非零向量α1，…，αs∈V，使得

证 （i）由前面的讨论可知，存在非零向量α∈V，使得V＝C（φ，α）当且仅当φ的不变因子组为1，…，1，f（λ）．改写（ii）为：

（ii）k＝max｛s∈Z＋｜存在非零向量α1，…，αs∈V，使得，只要证明：由（i）可推出k≥r；由（ii）可推出r≥k，于是有k＝r，因此（i）与（ii）等价．

假设（i）成立，因为初等因子组是相似关系下的全系不变量，故由［2］的例7．2可知，存在直和分解，使得的不变因子组为于是存在使得Vi从而

假设（ii）成立，设dimC（φ，αi）＝ni，则由引理1可知，是C（φ，αi）的一组基．于是是V的一组基，φ在这组基下的表示矩阵为

其中fi（λ）是φ限制在C（φ，αi）上的特征多项式，F（fi（λ））是fi（λ）的友阵．一方面考察特征多项式，有f（λ）＝f1（λ）…fk（λ）；另一方面考察极小多项式，由［1］的命题6．3．3可知，f（λ）是f1（λ），…，fk（λ）的最小公倍式，因此f1（λ），…，fk（λ）必两两互素，于是f（λ）的互异的首一不可约因式至少有k个，从而r≥k．

其中Jri（λi）是如下ri阶的Jordan块：

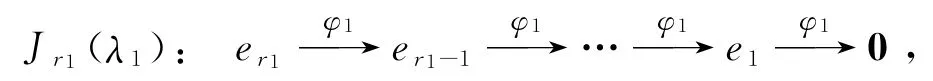
这说明第一个Jordan块Jr1（λ1）对应的子空间V1＝L（e1，e2，…，er1）就是由er1生成的循环子空间C（φ1，er1）．因此全空间V可以分解为若干个基向量生成的循环子空间的直和：

注意到φi＝φ｜Vi－λiIVi，其中Vi是第i个Jordan块对应的子空间，因此上述循环子空间都是关于不同线性变换的循环子空间，而且每一个循环轨道（上述关系图）都是以零向量结尾，这些都是与有理标准形诱导的循环子空间直和分解不同的．

下面利用Jordan块对应的循环子空间来给出两个有趣的应用．

推论3 设A＝Jn（λ0）是特征值为λ0的n阶Jordan块，B为同阶方阵，若AB＝BA，则存在次数小于n的多项式g（λ），使得B＝g（A）．

证 用几何的语言来证明．设φ是n维复线性空间V上的线性变换，φ在V的一组基｛e1，e2，…，en｝下的表示矩阵是Jordan标准形Jn（λ0），ψ是另一线性变换且与φ可交换，令φ0＝φ－λ0IV，则V＝C（φ0，en）为循环空间且φ0ψ＝ψφ0．由引理2（2）可知，存在次数小于n的多项式g0（λ），使得ψ＝g0（φ0），令g（λ）＝g0（λ－λ0），则ψ＝g（φ）．

如果已知n阶方阵A的Jordan标准形为J＝diag｛Jr1（λ1），Jr2（λ2），…，Jrk（λk）｝，一个自然的问题是，对任意的正整数m，Am的Jordan标准型如何确定？要回答这个问题，只要对Jordan块Jn（λ0）来考虑即可．若λ0≠0，则通过Jordan标准形理论不难证明Jn（λ0）m的Jordan标准形是（参考［2］的例7．35）；若要考虑Jn（0）m的Jordan标准形，如用代数的方法，则需要通过矩阵的秩与Jordan块个数的关系来得到结论（参考［2］的例7．33和例7．36）．在这里我们将通过Jordan块对应的循环子空间来给出上述问题的几何解法．

例1 求Jn（0）m（m≥1）的Jordan标准形．

解 若m≥n，则Jn（0）m＝O．以下可设m＜n，并作带余除法n＝mq＋r，其中0≤r＜m．用几何的语言来考虑，设φ是n维复线性空间V上的线性变换，φ在V的一组基｛e1，e2，…，en｝下的表示矩阵是Jordan标准形Jn（0），则V＝C（φ，en）为循环空间．由φm可诱导出如下的循环轨道：是K上的不可约多项式，用反证法来证明结论．若任取Im（φψ－ψφ）中的非零向量α，则Im（φψ－ψφ）＝L（α）．因为φ的特征多项式f（λ）在K上不可约，由命题1充分性的证明可得V＝C（φ，α），再由引理1可知，｛α，φ（α），…，φn－1（α）｝是V的一组基．设线性变换φψ－ψφ在这组基下的表示矩阵为C＝（cij），则由Im（φψ－ψφ）＝L（α）可得cij＝0对任意的i＞1成立，于是

一般地，对任意的k≥1，考虑线性变换（φψ－ψφ）φk－1在上述基下的表示矩阵，这是一个从第二行开始都为零且第（1，1）元素等于c1k的矩阵，于是

从而C＝O，即φψ－ψφ＝0，这与r（φψ－ψφ）＝1相矛盾．

注意到命题1，推论2和例2中都有不可约多项式的条件，因此利用互素多项式的性质也可以给出上述题目的其他证明（推论2的另证可参考［2］的例5．76）；另外，推论1和推论3也有代数的证明（可参考［2］的例7．22和例7．23）．可能某些证明要比本文中的证明更简单，然而循环子空间的方法却给出了清晰的几何意义，让学生们能通过几何直观抓住问题的本质，从而加深对问题的理解，最终找到解决问题的有效途径．事实上，这也是复旦大学数学科学学院高等代数教学中的一条主线，即在要求学生熟练掌握代数方法的同时，也要求学生深入理解概念和定理的几何意义，强调代数与几何之间的相互转换和有机统一，而本文所阐述的循环子空间的若干应用正是从一个侧面反映了这种理念在高等代数教学中的实践．

致谢 在本文的撰写过程中，得到了复旦大学数学科学学院姚慕生教授、吴泉水教授、朱胜林教授的热心指导和大力斧正，在此谨表示衷心的感谢．

由循环轨道与Jordan块之间的对应可知，只要将旧基｛e1，e2，…，en｝按照上述循环轨道进行重排，则φm在新基｛er，…，en－m，en；…；e1，…，en－r＋1－m，en－r＋1；em，…，en－r－m，en－r；…；er＋1，…，en－2 m＋1，en－m＋1｝下的表示矩阵为diag｛Jq＋1（0），…，Jq＋1（0），Jq（0），…，Jq（0）｝，其中有r个Jq＋1（0），m－r个Jq（0）．由Jordan标准形的唯一性可知，这就是φm或Jn（0）m的Jordan标准形．

最后，给出一个综合运用循环子空间理论的例题．

例2 设A，B是数域K上的n阶方阵，且A的特征多项式f（λ）是K上的不可约多项式，证明：r（AB－BA）≠1．

证 换成几何的语言来证明，设V是数域K上的n维线性空间，φ，ψ是V上的线性变换，

［参 考 文 献］

［1］ 姚慕生，吴泉水，谢启鸿．高等代数学［M］．3版．上海：复旦大学出版社，2014．

［2］ 姚慕生，谢启鸿．高等代数（大学数学学习方法指导丛书）［M］．3版．上海：复旦大学出版社，2015．

Construction of LDPC Code Based on Self－dual Code

CHAO Hai－zhou1， Ni Xiang－fei2
（1．Department of Basic Courses，Shanghai University of Finance ＆Economics Zhejiang College，Jinhua Zhejiang 321013，China；2．Department of Mathematics，Zhejiang Normal University，Jinhua Zhejiang 321001，China）

CLC Number：O29 Document Code：A Article ID：1672－1454（2016）01－0007－04

Received date：2015－05－20

Foundation item：National Science Foundation of China（11401534），（11226050）and（61272007）

1　Introduction

Low density parity check codes were firstly introduced by R．G．Gallager in 1962［1］．These classes of codes can be defined by very sparse parity matrix．For their decoding performance are near to the Shannon limit［2－3］，LDPC codes were investigated wildly．There are two classes of LDPC codes．If the parity check matrix has weight kin each row and weight l in each column exactly，the code can be called（k，l）－regular LDPC code and irregular otherwise．

Two methods can be used to construct LDPC codes：random or pseudo－random ways and algebraic way．In general，irregular LDPC codes constructed by random or pseudo－random ways have been shown surpassing performance in AWGN channel than regular LDPC codes generated by algebraic way when the code has more long length．But these methods also face to its shortage．With losing of structure，the complexity will increase unavoidably both of encoding and decoding proceedings．So the requirement will be high both for hardware and software．

LDPC codes can be formed from Reed－Solomon code［4］，which is a typical block code．It is an useful way to construct LDPC codes from other good codes．

A code is self－dual if the generator matrix of the code identifies its parity check matrix．It implies that the code has rate 1／2．In［5］，an useful way to generate self－dual code fromq－ary circulant matrices based on orthogonal design has been introduced．In this paper，we will build binary LDPC code from the generator matrix of the q－ary self－dual code．

2　Code Construction

Let GF（q）be a Galois field with qelements andαbe a primitive element of GF（q）．If we denoteα－∞＝0，then all elements of GF（q）can be presented asα0＝1，α1，α2，…，αq－2，α－∞＝0．We can make a one－one corresponding between elements of GF（q）and a subset of（q－1）－dimensional vector space Rq－1on real number field by a function Z．

Definition 2．1 The function

is calledα－location vector function on GF（q），where

The vector corresponding toαiis called the location vector［4］ofαi．Given a q－ary matrix，the function Zcan be generalized to deal with a matrix．

Given a q－ary circulant matrix A，if there exists a circulant matrix Bsuch that

then a self－dual code can be generated by the following matrix［5］

Based on the generator matrix of self－dual code，we can construct a LDPC code byα－location vector function．

Proposition 2．1 Let Gbe a generator matrix of a q－ary self－dual code in the form of（a）and H arise fromby deleting its all－zero columns．Thenis a parity check matrices of a LDPC code．

Obviously，I2nwill be remained，whendelete its all－zero columns．It implies that rows ofare linear independence and the number of columns ofis at most

Hence the maximum rate of the codes is

But for the existence of all－zero columns in the second half of the matrix，the value of the maximum rate can hardly be achieved．

Now we will calculate the length and rate of the code．

Let a1，a2，…，ambe a sequence comes fromGF（q）．The set Dis composed of all different nonzero elements of a1，a2，…，am．If we denote the number of elements in Dby l（a1，a2，…，am），then

Lemma 2．2 The number of all non－zero columns of（Z（a1）T，Z（a2）T，…，Z（am）T）Tis l（a1，a2，…，am）．

Proof Letαbe a primitive element in GF（q）and aibe a power ofα．If ai≠aj，then location vectors of aiand ajare distinct．So 1stays in different positions of their location vectors．If b∈GF（q）and b∉D，then the corresponding columns of b in（Z（a1）T，Z（a2）T，…，Z（am）T）Tare all zero．Otherwise，location vector of b appear and there is a 1in the right place．It implies that b∈D，contradictorily．

The formulation of length Land rate Rof the code corresponding tois

and then the rate of the code Ris are given by：

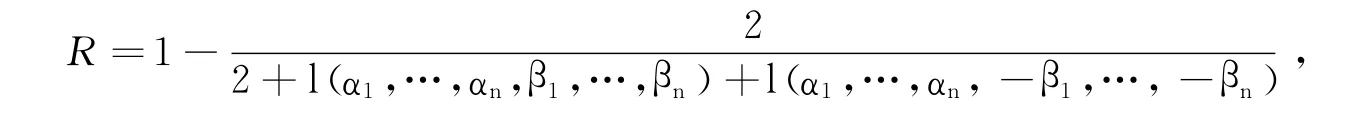
Theorem 2．3 The length Lof the LDPC code corresponding to

where（α1，…，αn），（β1，…，βn）are first rows of Aand Brespectively．

Proof Because Aand Bare all circulant，ATand－BTare circulant．Then all columns of Aand ATare composed of（α1，…，αn），all columns of Bare composed of（β1，…，βn）and all columns of－BTare composed of（－β1，…，－βn）．We only need to observe first rows of（A，B）and（A，－B）respectively．By lemma 2．2，the conclusion is straightforward．

The following corollary shows the region of R．

Proof We consider two especial cases．Firstly，if A＝Inand B＝O，then the rate reach low bound．

S

econdly，if first rows of（A，B）and（A，－B）contain all q－1nonzero elements of GF（q），then the rate can attain the upper bound

As an example，by computer searching，when n＝4and q＝11，we have

Example 2．1 When is 60and the rate of the code is 0．8667．The code hasn’t the largest rate and the longest length in the situation that self－dual codes have length 16on GF（11）．But if we ignore the identity matrix in the front of

the length of the code corresponding to，the remain satisfy RC－constraint by computer testing．

If the generator matrix of a code can be gained just by elementary transformation of rows and columns from another one’s，two codes are called equivalent．In general，self－dual codes with the same length are not unique under equivalence relationship．Suppose that there are Ninequivalent selfdual codes in the form of（a）with length n．We choose integer numbers s and t satisfying st≤N．Thenst inequivalent self－dual codes with length ncan be selected out for arranging a matrix G＊with their generator matrices as G＊′s elements．Now we replace everyαiby their location vectors and delete columns with all 0elements．We have a parity check matrix of LDPC codes．

Proposition 2．5 Let Gij（i＝1，…，s；j＝1，…t）be generator matrices of self－dual codes in the form of（a），which are inequivalent each other．Denote G＊＝（Gij）s×t．Letis arisen fromZ（G＊）by deleting its all－zero columns．Thenis parity check matrix for some LDPC code．

3　Conclusion

•Based on self－dual codes with length 4n，we have the main method of constructing LDPC codes from theα－location vector function of generator matrix of self－dual codes．

•By considering the first row of generator matrix of the corresponding self－dual code，we investigate the length and the rate of LDPC code，and show the range of rates of this codes．

•To expand the method，we consider all inequivalent self－dual codes with the same size as cells，constructing a more large matrix．The size of LDPC code can be more adaptable．

•By computer searching，when n＝4and q＝11，the superior code with high rate have been found．

The method shows a way to search codes with high rate and good algebraic structure．

［References］

［1］ Gallager RG．Low Density Parity Check Codes［M］．Cambridge，MA：MIT Press，1963．

［2］ Shannon CE．A mathematical theory of communication［J］．Bell systems Technology Journal，1948，27：379－423．

［3］ Chung S，Forney GD，Richardson JJ and Urbanke R．On the design of low－denisty parity－check codes within 0．0045 db of the Shannon limit［J］．IEEE Commun．Lett．，2001，5：58－60．

［4］ Djurdjevic I，Xu J，Abdel－Ghaffar K and Lin S．A class of Low－density parity－check codes Constructed based on Reed－Solomon codes with two information symbols［J］．IEEE Commun．Lett．，2003，7：317－319．

［5］ Koichi Betsumiya，Telio Georgiou，Aron Gulliver T，Masaaki Harada and Christos Koukouvinos．On self－Dual Codes over Some Prime Fields［J］．Discrete Math．，2003，262：37－58．

Some Applications of Cyclic Subspaces

XIE Qi－hong
（School of Mathematical Sciences，Fudan University，Shanghai 200433，China）

Abstract：By means of cyclic subspaces induced by a linear transformation，we reprove the Cayley－Hamilton theorem，and give some applications to certain problems in the theory of similarity of matrices． A new method for constructing LDPC codes based on self－dual code is introduced．Rates and lengths of these codes are analyzed．Code with high rate and good property in this class has been searched out by using MATLAB when the length of self－dual code on GF（11）is 16．

Key words：linear transformation；invariant subspace；cyclic subspace；Cayley－Hamilton theorem；rational canonical form；Jordan canonical form LDPC code；self－dual code；α－location vector function；algebraic coding theory；generator matrix

［基金项目］国家自然科学基金项目（11422101）

［收稿日期］2015－09－16

［中图分类号］O151．21

［文献标识码］A

［文章编号］1672－1454（2016）01－0001－06