夯实基础，大胆尝试、猜想、反思

江叔新

摘 要：在创新的前提下，本文主要阐述定义性阅读题解法一点思考以及四道典型题目的解题过程。

关键词：创新；定义性阅读；应用；解法

近年来，由于素质教育的实施速度加快，各种评价也随之变革，现在的评价更多侧重于创新能力和学习能力方面。纵观这些年来各地中考试卷，几乎都能见到创新题型，而在众多的创新题中有一类题目特别突出，那就是定义性阅读理解题。这类题目多为几何题，它往往与课本知识联系很紧密，但是又涉及很多新鲜的数学规定、数学术语。它考查的是学生的阅读能力、理解能力，知识的迁移能力，以及应用已有的知识解决后面的练习的应用能力。这往往给我们的学生带来很大的挑战，许多学生不知道从何处开始分析，从而失掉了解题的契机。笔者现就这类问题的解决提出一点自己的看法。

例1：（北京中考卷压轴题）我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形。请解答下列问题：

（1）写出你所学过的特殊四边形中等对角线四边形的两种图形的名称；

（2）探究：当等对角成四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论。

第一问的分析：抓住题目中关键词“四边形”、“对角线相等”，马上联想到我们学过的四边形，普通四边形、平行四边形、矩形、菱形、正方形、梯形、直角梯形、等腰梯形，再分析这些四边形的对角线的特征，普通四边形对角线特征不知，平行四边形对角线互相平分，矩形对角线互相平分且相等，菱形对角线互相垂直，正方形对角线互相平分、互相垂直且相等，每条对角线平分一组对角，普通梯形对角线特征不明朗，等腰梯形对角线相等。这简单的第一问考查了我们学过的所有特殊四边形的对角线的特征，如此第一问顺利解决了。

第二问才是真正的探索的重点，创新的关键。从特殊的等对角四边形、矩形（或正方形或等腰梯形）着手考虑。

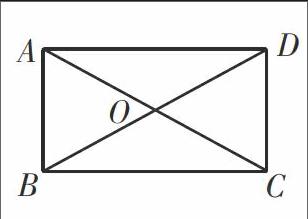
如图：∠AOB=∠DOC=60°，则由OB=OA，OC=OD，

∴△AOB为正三角形，△COD为正三角形，AB=AO，CD=OC，∴AB+CD=AC。

（或者利用30°所对直角边等于斜边的一半）

如此可以判定此题中这个关系中应有相等这一种答案，再分析等腰梯形。

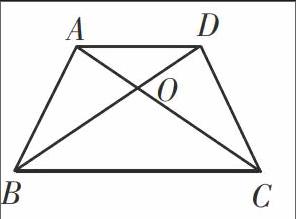
考虑特殊情况：∠ODC=90°，∠AOB=60°。∠ABO=∠DCO=30°。

∠BAO=90时°，设OD=x时，

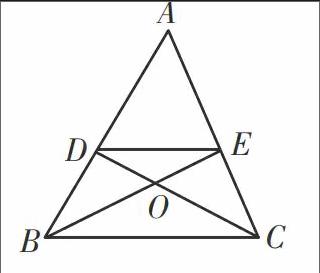
也许读者心头会不由自主地涌出如下一种情形：AB+CD

例2：（2007年北京市中考压轴题）我们知道：有两条边相等的三角形叫作等腰三角形，类似地，我们定义：至少有一组对边相等的四边形叫作等对边四边形。

（1）请写出一个你学过的特殊四边形中是等对边四边形的图形名称；

（2）如图，在△ABC中，点D、E分别在AB、AC上，设CD、BE相交于点O，若∠A=60°，∠DCB=∠EBC=12∠A，请你写出图中一个与∠A相等的角，并猜想图中哪个四边形是等对边四边形。

（3）在△ABC中，如果∠A不等于60°的锐角，点D、E分别在AB、AC上，且∠DCB=∠EBC=12∠A，探究满足上述条件的图形中是否存在等对边四边形，并证明你的结论。

此题在上年中考题的基础上继续考查了四边形的相关知识，并且又是给出一个新的定义，要求我们去探索证明。这两道题目可以说是一脉相承，其中都有60°这个特殊条件，这也启发了我们可以从此着手联系30°、120°等可能的角度，此题的关键是证明有两边相等，常规的方法是证明三角形全等，那么作辅助线就是一个突破口，多次尝试总可以找到正确的辅助线，过B、C分别作直线CD、BE的垂线段，然后利用全等解决问题。

例3：（2006年安徽中考最后一题）：如图1，凸四边形ABCD，如果点D满足∠APD=∠APB=α，且∠BPC=∠CPD=β，则称点P为四边形ABCD的一个半等角点。

（1）在图2正方形ABCD内画一个半等角点P，且满足α≠β；

（2）在图3的四边形ABCD中画一个半等角点P，保留画图痕迹；

（3）若四边形ABCD有两个半等角点P1、P2（如图4），证明线段P1P2上任一点也是它的半等角点。

此题难度更大，是一道极好的中考选拔题，把数学学习能力强弱的学生区分开来。中考的一个作用就是选拔有较强学习能力和学习天赋的学生进入高一级学校学习。要想解决这一道题目需要学生能够读懂题目，并且还要能够把新定义和已有知识糅合起来好好运用，如正方形中来找半等角点很容易，但要求α≠β就要注意了。在图3中利用尺规作图来找一个半等角点，这需要仔细分析图1中的特征和自己积累的数学思想和数学意识来寻找解决办法。连结AC，过B作关于AC的对称点B，连结DB并延长DB与AC的交点就是一个半等角点。这里需要用到尺规作图知识和对称点的思想加以指导。而第三问更加综合了，需要大胆猜想，并加以验证。①A、P1、P2、C四点共线；②DP1=BP1，DP2=BP2；③P1P2上任取一点P，△P1PB≌△P1PD，从而∠APD=∠APB，∠DPC=∠BPC，从而P是半等角点。

例4：（宁波市2007年中考最后一题）：四边形一条对角线所在直线上的点，如果到这条对角线两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点。如图1，点P为四边形ABCD对角线AC所在直线上的一点，PD=PB，PA≠PC，则点P为四边形ABCD的准等距点。

（1）如图2，画出菱形ABCD的一个准距点；

（2）如图3，做出四边形ABCD的一个准距点（尺规作图，保留作图痕迹，不要求写作法）。

（3）如图4，在四边形ABCD中，P是AC上的点，PA≠PC，延长BP交CD于点E，延长DP交BC于点F，且∠CDF=∠CBE，CE=CF，求证：点P是四边形ABCD的准等距点。

（4）试研究四边形的准等距点个数的情况（说出相应的四边形的特征及准等距点的个数，不必证明）。

相信此题已经引起了很多教师的兴趣，其解法也是人人皆知了。这四个问题的设置是一问难过一问，有的学生没有耐心读题的习惯，连第一问也做不出来，更不要说后面几问了。这也反映了我们学生平时的学习习惯，做事很急躁，总是想一下做出答案。如果不能静下心来思考、分析，那么很难全部做对。我们要加强平时的训练，做题目前要多看几遍题目，读懂了题目再动手。并且要求解题时仔细一些，考虑问题全面一些。这需要时间，更需要有耐心和恒心。素质教育就要求学生有独立思考的能力，更需要学生有顽强的毅力和不断攻克难关的决心。社会需要具备这些素质的人才。

面对新题目、新题型，学生一定要学会适应。我们教师在平常的教学活动中一定要有意识地培养学生的学习能力特别是自学能力。我们要多多总结一些好的学习方法，当然更应该鼓励学生自己去试探、总结、归纳，形成自己的解题习惯。解题方法千千万，探索的道路要靠自己去走。

参考文献：

1.天利38套.

2.数学课程标准.

（作者单位：浙江省余姚市三七市镇中学）