空间曲线绕任意轴的旋转面面积

陈珍培

(浙江树人大学基础部,浙江杭州310015)



空间曲线绕任意轴的旋转面面积

陈珍培

(浙江树人大学基础部,浙江杭州310015)

[摘要]利用向量和定积分的知识,解决了空间曲线绕任意轴旋转所得旋转面的面积计算问题,给出了旋转面面积的简明计算公式,并借助实例进行说明.

[关键词]旋转面； 行列式； 向量； 定积分

有关旋转面面积的计算问题,一般教科书只讨论坐标平面内的母线绕坐标轴旋转的情形, 至于坐标平面内的母线绕坐标面内斜轴旋转的情形，也大量地出现在有关的文献中,见文[1]，[2]等.至于空间曲线绕空间任意轴的旋转面面积，由于计算相当复杂，至今尚未有完善的计算公式.文[3]所讨论的旋转面虽然以空间直线为旋转轴，但要求母线与旋转轴共面，至于母线与旋转轴不共面的情形,则未曾提及；文[4]虽然给出了空间母线绕空间任意轴的旋转面面积公式，但由于是通过坐标旋转进行推算，造成积分公式篇幅过于巨大，不利于具体的计算.本文对空间曲线绕空间任意轴的旋转面面积进行分析，并得到简洁而完美的旋转面面积公式.

1任意旋转面面积公式的推导

公式设Γ：x=x(t),y=y(t),z=z(t) (α≤t≤β)为光滑的空间曲线段，直线l经过原点且以s=(a,b,c)为单位方向向量(|s|=1).若Γ上任意两部分产生的旋转面都不重合，则Γ绕l旋转所得的旋转面面积为

(1)

其中

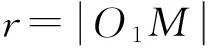
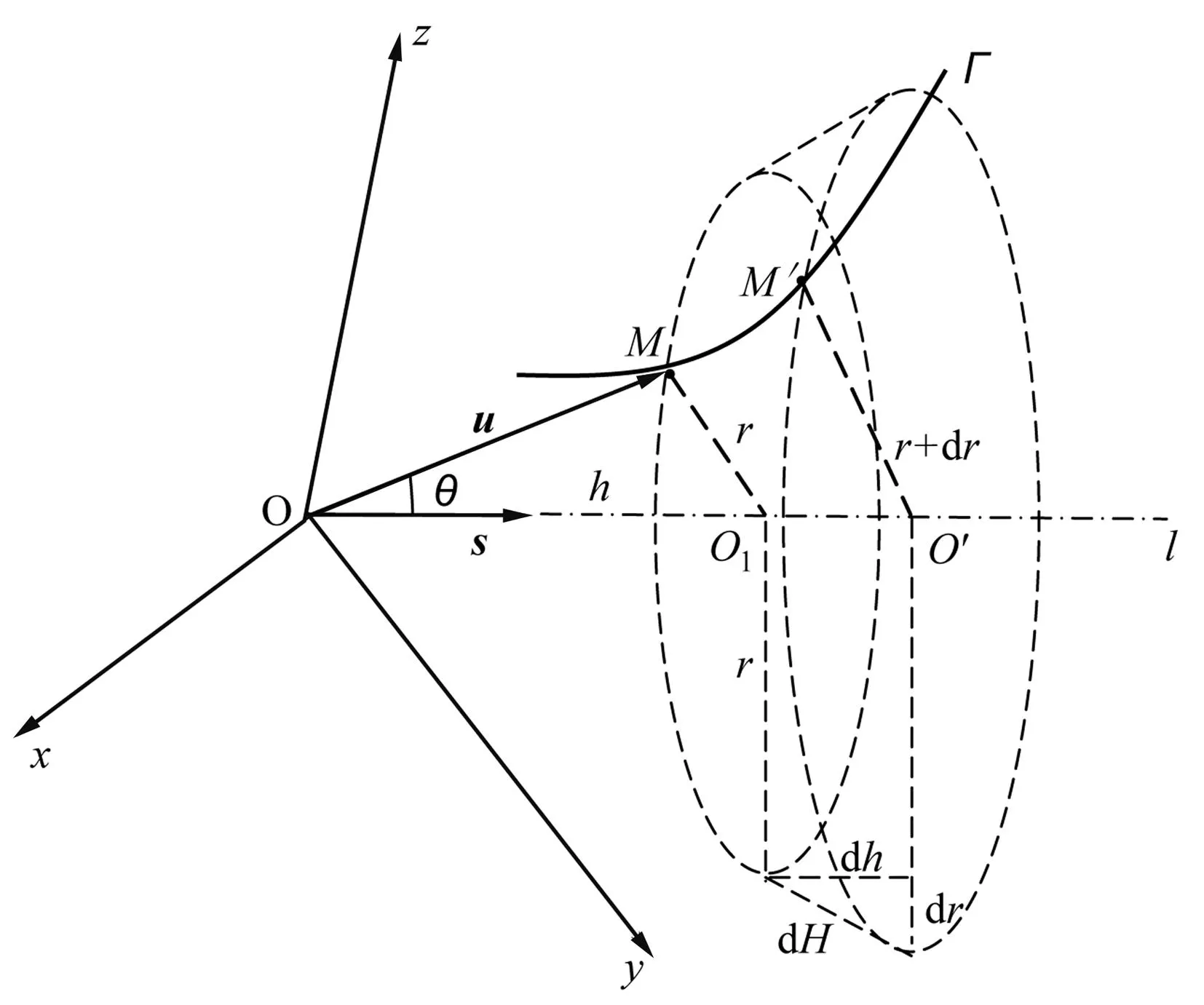
图1　公式证明示意图

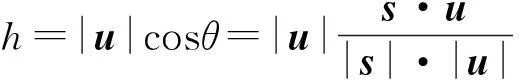
若记

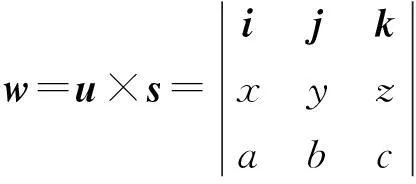
其中

M1=cy-bz,M2=cx-az,M3=bx-ay，

(2)

则截面圆半径

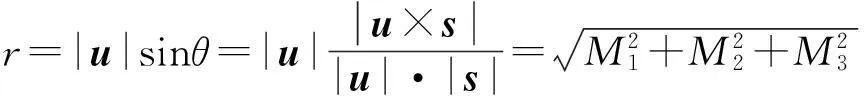
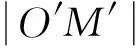
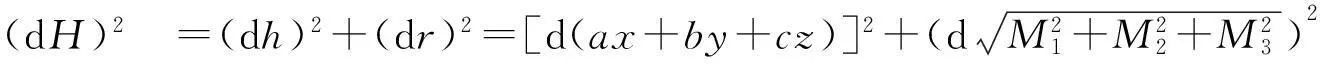
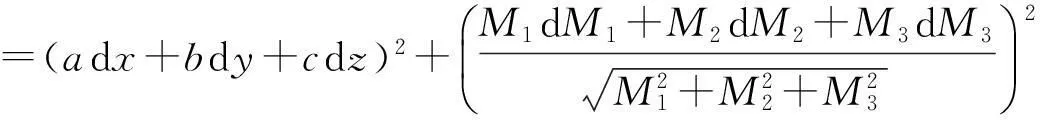
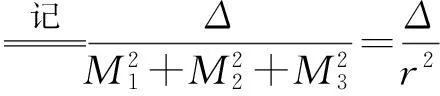
(3)

其中

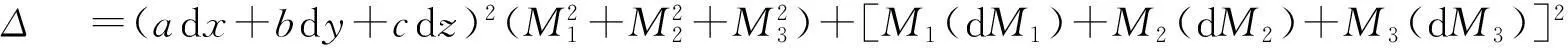
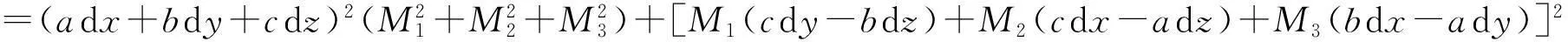
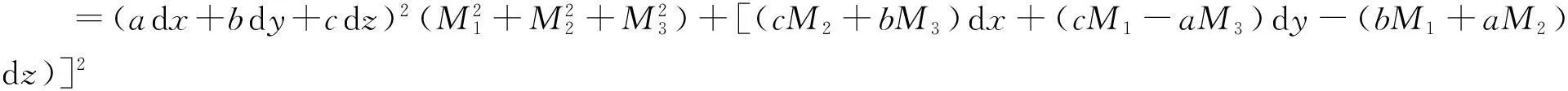
=K1(dx)2+K2(dy)2+K3(dz)2+K4dxdy+K5dydz+K6dzdx，

(4)

其中

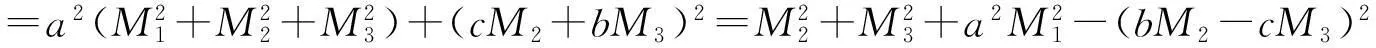
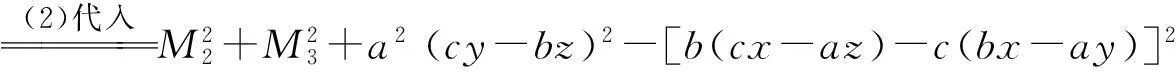
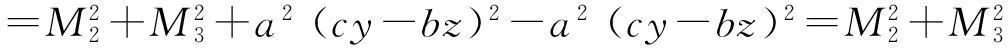
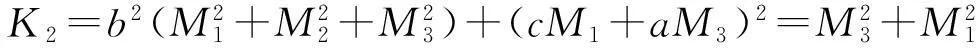
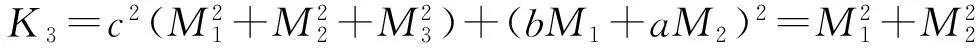
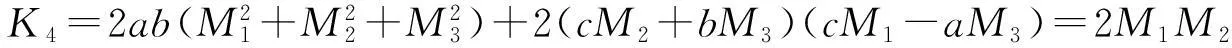
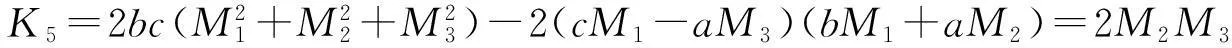
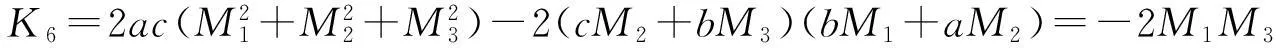
(以上K2,…,K6的化简过程与K1类似).将K1,…,K6代入(4)，可得

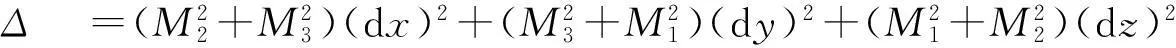
+2M1M2dxdy+2M2M3dydz-2M1M3dzdx

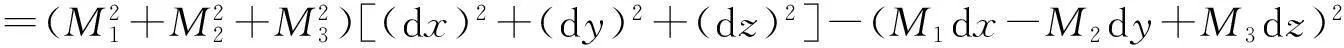
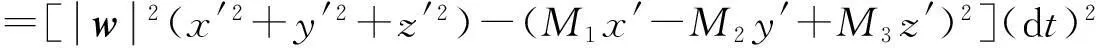
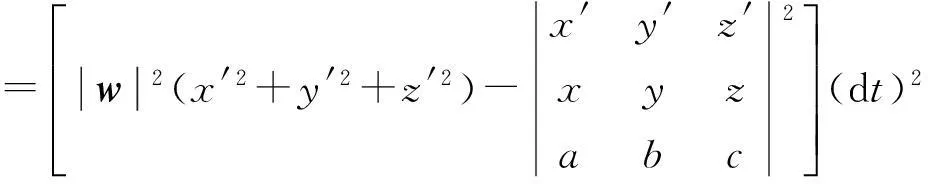
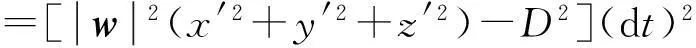
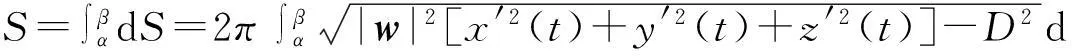
推论1若旋转轴l的方向向量s=(a,b,c)不是单位向量，则旋转面面积为

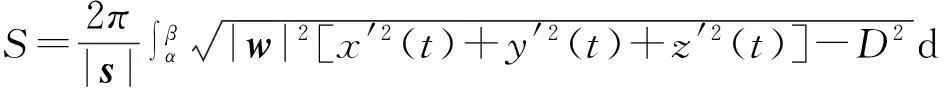
(4)

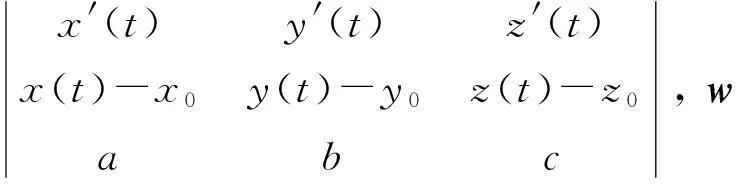
2应用举例

解显然旋转轴的方向向量为s=(a,b,c)=(1,1,1)，

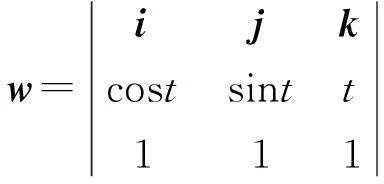
|w|2=2(1+t2)-2t(sint+cost)-sin2t，

x′2(t)+y′2(t)+z′2(t)=2，

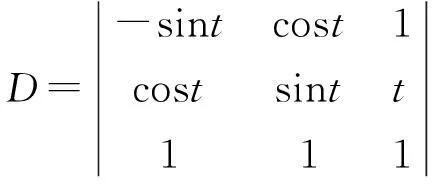
将上述结果代入(4)可得旋转面的面积为

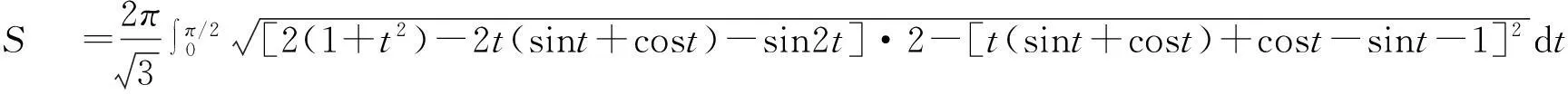
≈6.9704.

面积的计算结果是借助数学软件Matlab得到的.

[参考文献]

[1]储理才.一个计算旋转曲面面积的积分公式[J].高等数学研究,2001,4(1):13-14.

[2]吴旭亭.平面图形绕斜轴旋转所成旋转体的体积与侧面积[J].师茅师范高等专科学校学报,2005, 21(3):57-58.

[3]李艳丽,王骋.旋转曲面面积的计算方法[J].纺织高校基础学科学报,2008,21(3):280-283.

[4]聂智.旋转面面积与旋转体体积的积分公式[J].渝西学院学报,2003,2(3)：5-9.

The Area of Surface of Revolution formed by Revolving

the Space Curve around the Arbitrary Axis

CHENZhen-pei

(Basic Courses Dept of Zhejiang Shuren University,Hangzhou, Zhejiang 310015,China)

Abstract:Based on the knowledge of vector and definite integration, the problem of area of the surface of revolution formed by revolving the space curve around the arbitrary axis be solutioned. A figure about area of revolution is obtained. An example be provided to demonstrate application of the figures.

Key words:surface of revolution; determinant; vector; definite integration

[收稿日期]2014-06-01

[中图分类号]O172.2

[文献标识码]C

[文章编号]1672-1454(2015)01-0121-03